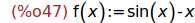
Tema CS2: Funciones de una variable
(Ejercicios resueltos)

1 Definición de funciones

Ejercicio 1.1. Definir, usando el operador :=, la función
   f(x) = sen(x)-x

(%i47) f(x):=sin(x)-x;

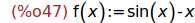
Ejercicio 1.2. Definir, usando lambda, la función g que a un x le asigna
sen(x).

(%i48) g:lambda([x],sin(x));

Ejercicio 1.3. Definir, usando define, la función
   h(x) = sqrt(1+x^2)-2*x

(%i49) define(h(x),sqrt(1+x^2)-2*x);

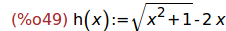
2 Límites y asíntotas

Ejercicio 2.1. Calcular el límite de f(x) cuando x tiende a infinito.

(%i50) limit(f(x),x,inf);

Ejercicio 2.2. Calcular el límite de g(x)/x cuando x tiende a cero.

(%i51) limit(g(x)/x,x,0);

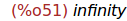
Ejercicio 2.3. Calcular el límite de h(x) cuando x tiende a menos infinito.

(%i52) limit(h(x),x,minf);

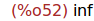
Ejercicio 2.4. Calcular el límite de 1/(1-t^2) cuando t tiende a 1 por la
izquierda.

(%i53) 'limit(1/(1-t^2),t,1,minus)=limit(1/(1-t^2),t,1,minus);

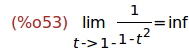
Nota: Cuando una expresión va precedida del operador quote ('), significa
que dicha expresión no se evalúa.

Ejercicio 2.5. Calcular el límite de 1/(1-t^2) cuando t tiende a 1 por la
derecha.

(%i54) 'limit(1/(1-t^2),t,1,plus)=limit(1/(1-t^2),t,1,plus);

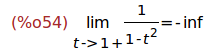
Ejercicio 2.6. Calcular los 2 primeros términos del polinomio de Taylor de
h(x) en un entorno del infinito y, a partir de él, el límite de h(x)
x cuando x tiende a infinito.

(%i55) taylor(h(x),x,inf,2);

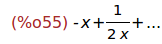
(%i56) limit(%, x, inf);

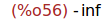
3 Derivación

Ejercicio 3.1. Calcular la derivada de h(x) respecto de x.

(%i57) 'diff(h(x),x)=diff(h(x),x);

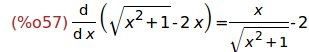
Ejercicio 3.2. Definir, usando define, la función p(x) como la derivada
de h(x) respecto de x.

(%i58) define(p(x),diff(h(x),x));

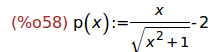
(%i59) define(p(x),ratsimp(diff(h(x),x)));

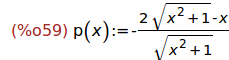
Ejercicio 3.3. Calcular segunda la derivada de la función f respecto de x.

(%i60) diff(f(x),x,2);

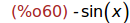
Ejercicio 3.4. Calcular la ecuación reducida de la tangente a la curva
definida por h, en el punto de abcisa x=2.

(%i61) y=expand(taylor(h(x),x,2,1));

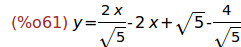
4 Funciones definidas a trozos

Ejercicio 4.1. Definir la función
   d(x) = 0, si x < 0
        = x^3, si 0 <= x <= 1
        = 1, si x > 1

(%i62) d(x) := if x<0 then 0
           elseif x<=1 then x^3
           else 1;

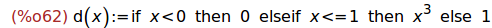
5 Representación gráfica

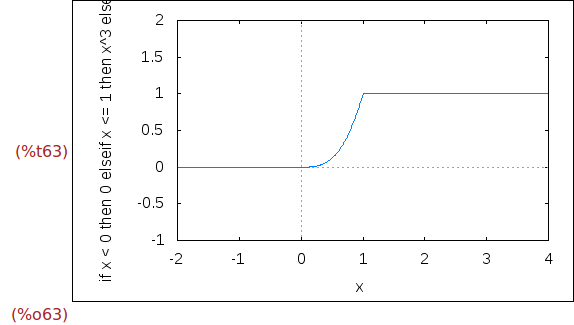
Ejercicio 5.1. Dibujar la gráfica de d(x) para x entre -2 y 4 e y entre
-1 y 2.

(%i63) wxplot2d(d(x), [x,-2,4], [y,-1,2]);

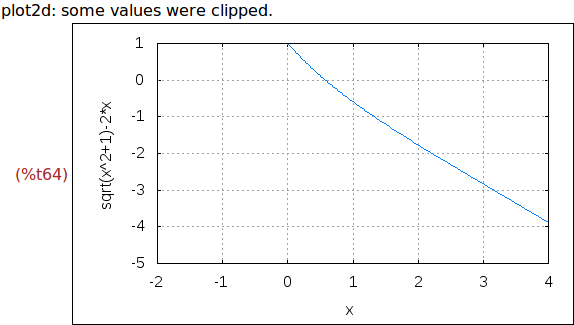
Ejercicio 5.2. Dibujar la gráfica de h(x) para x entre -2 y 4 e y entre
-5 y 1, usando retícula.

(%i64) wxplot2d(h(x), [x,-2,4], [y,-5,1], [gnuplot_preamble, "set grid "])$

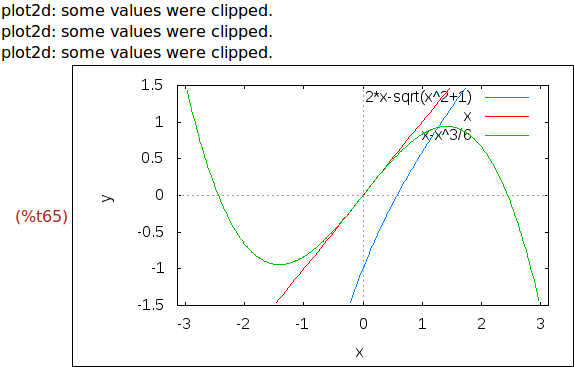
Ejercicio 5.3. Dibujar las gráficas de g(x), x y x-x^3/6 para x entre
pi y pi e y entre -1.5 y 1-5, mostrando los ejes de coordenadas.

(%i65) wxplot2d( [g(x),x,x-x^3/6] , [x,-%pi,%pi] , [y,-1.5,1.5] ,
 [gnuplot_preamble, "set zeroaxis"])$

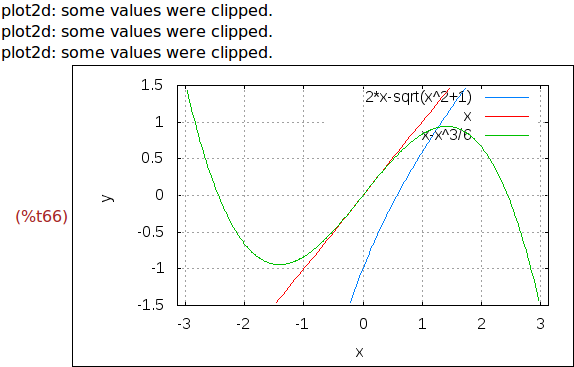
Ejercicio 5.4. Dibujar las gráficas de g(x), x y x-x^3/6 para x entre
pi y pi e y entre -1.5 y 1-5, mostrando los ejes de coordenadas y
retículas.

(%i66) wxplot2d( [g(x),x,x-x^3/6] , [x,-%pi,%pi] , [y,-1.5,1.5] ,
 [gnuplot_preamble, "set zeroaxis; set grid"])$