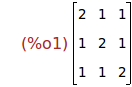
Tema CS6: Matrices con Maxima
(Ejercicios resueltos)

1 Definición de una matriz

Ejercicio 1.1. Definir la matriz M
   [2 1 1]
   [1 2 1]
   [1 1 2]

(%i1) M:matrix([2,1,1],[1,2,1],[1,1,2]);

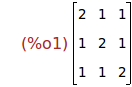
Ejercicio 1.2. Definir la matriz N
   [2 0 3]
   [4 1 5]

(%i2) N:matrix([2,0,3],[4,1,5]);

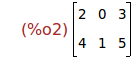
Ejercicio 1.3. Definir la matriz A de orden 3x3 cuyo elemento (i,j) es
(-1)^(i+j)/(i+j)

(%i3) a[i,j]:=(-1)^(i+j)/(i+j) $

(%i4) A:genmatrix(a,3,3);

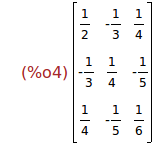
Ejercicio 1.4. Definir la matriz B de orden 2x2.

(%i5) B:genmatrix(b,2,2);

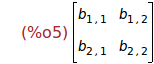
2 Operaciones con matrices

Ejercicio 2.1. Calcular la suma de las matrices M y 2*A

(%i6) M+2*A ;

Ejercicio 2.2. Calcular el producto de las matrices M y N.

(%i7) N.M;

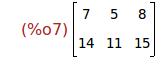
Ejercicio 2.3. Calcular la potencia 5º de la matriz M.

(%i8) M^^5;

Ejercicio 2.4. Calcular el rango de la matriz N.

(%i9) rank(N);

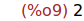
Ejercicio 2.5. Calcular el determinante de la matriz A.

(%i10) determinant(A);

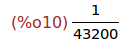
Ejercicio 2.6. Calcular la inversa de la matriz A.

(%i11) invert(A);

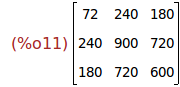
Ejercicio 2.7. Calcular la traspuesta de la matriz N.

(%i12) transpose(N);

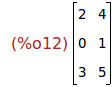
3 Diagonalización de matrices cuadradas

Ejercicio 3.1. Calcular el polinomio característico de la matriz M.

(%i13) charpoly(M,x);

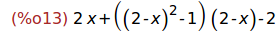
(%i14) expand(%);

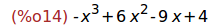
Ejercicio 3.2. Calcular los autovalores de la matriz M.

(%i15) solve(%=0,x) ;

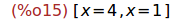
(%i24) factor(charpoly(M,x));

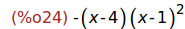
(%i17) eigenvalues(M);

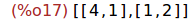
Ejercicio 3.3. Calcular los autovectores de la matriz M.

(%i18) eigenvectors(M);

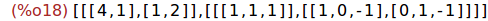
Ejercicio 3.4. Calcular la matriz P que es la matriz de paso de la base cacónica
de R3 a una base de autovectores.

(%i19) P:transpose( matrix([1,1,1],[1,0,-1],[0,1,-1]) ) ;

Ejercicio 3.5. Calcular la matriz Q que es la inversa de P

(%i20) Q:invert(P);

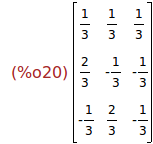
Ejercicio 3.6. Calcular la matriz diagonal D cuyos valores en la diagonal son
los autovalores de M.

(%i21) D:diag_matrix(4,1,1);

Ejercicio 3.7. Calcular el producto de las matrices P, D y Q.

(%i25) P.D.Q;

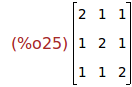
Ejercicio 3.8. Comprobar que el producto de las matrices P, D y Q es igual a la
matriz M.

(%i27) is(P.D.Q = M);

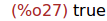
Fin.