La curva del dragón es un fractal que se construye siguiendo los siguientes pasos:

• A partir de un segmento, se construye el triángulo rectángulo e isósceles, como lo muestra las dos primeras figuras. Luego se borra el segmento inicial.
• Se repite varias veces el proceso de remplazar un segmento por otros dos para cada línea de la curva, alternando siempre la orientación de los triángulos.

La siguiente figura muestra los trece primeros pasos:

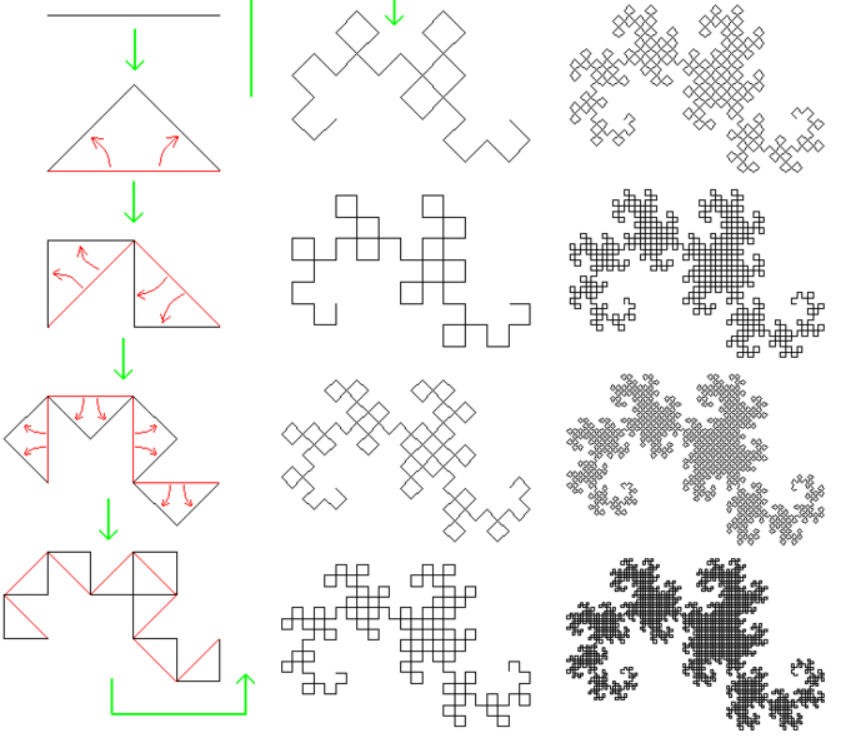
El ejercicio consiste en definir (en CodeWorld) la función

dragon :: Number -> Picture

tal que (dragon n) es el dibujo correspondiente al paso n de la construcción de la curva del dragón. Por ejemplo, el dibujo de dragon(20) es

Nota: La descripción de la curva dragón es la que se encuentra en el artículo de la Wikipedia.

Leer más…

Definir la función

adicionales :: Ord a => Int -> [a] -> [a] -> [a]

tal que (adicionales n xs ys) es la lista de los n elementos de que no pertenecen a ys (se supone que las listas xs e ys están ordenadas y que pueden ser infinitas). Por ejemplo,

adicionales 0 [1,3]   [1,3]                  ==  []
adicionales 1 [1,3]   [1]                    ==  [3]
adicionales 2 [1,3,5] [1]                    ==  [3,5]
adicionales 2 [1,3,5,7,9] [1,5,7]            ==  [3,9]
adicionales 2 ([1,3,5]++[7..]) ([1]++[7..])  ==  [3,5]

Leer más…

Las matrices se pueden representar de distintas formas. Por ejemplo, la matriz

|7 5 6|
|1 9 4|

se puede representar como la terna

([7,5,6,1,9,4],2,3)

(donde la primera componente es la lista de los elementos de matriz, la segunda es su número de filas y la tercera es su número de columnas) y también se puede representar como una lista de listas

[[[7,5,6],[1,9,4]]

(donde cada elemento es una de las filas de la matriz).

Definir las funciones

ternaAlistas :: ([a],Int,Int) -> [[a]]
listasAterna :: [[a]] -> ([a],Int,Int)

tales que ternaAlistas pase de la primera representación a la segunda y listasAterna pase de la segunda a la primera. Por ejemplo,

ternaAlistas ([7,5,6,1,9,4],2,3)  ==  [[7,5,6],[1,9,4]]
listasAterna [[7,5,6],[1,9,4]]    ==  ([7,5,6,1,9,4],2,3)
ternaAlistas ([7,5,6,1,9,4],3,2)  ==  [[7,5],[6,1],[9,4]]
listasAterna [[7,5],[6,1],[9,4]]  ==  ([7,5,6,1,9,4],3,2)

Leer más…

Definir la función

permutaConsecutivos :: [a] -> [a]

tal que (permutaConsecutivos xs) es la lista obtenida permutando los elementos consecutivos de xs. Por ejemplo,

permutaConsecutivos [1..8]         ==  [2,1,4,3,6,5,8,7]
permutaConsecutivos [1..9]         ==  [2,1,4,3,6,5,8,7,9]
permutaConsecutivos "simplemente"  ==  "ispmelemtne"

Leer más…

Para el juego de los bloques se dispone de un conjunto de bloques con una letra en cada una de sus dos caras. El objetivo del juego consiste en formar palabras sin que se pueda usar un bloque más de una vez y sin diferenciar mayúsculas de minúsculas. Por ejemplo, si se tiene tres bloques de forma que el 1º tiene las letras A y B, el 2ª la N y la O y el 3º la O y la A entonces se puede obtener la palabra ANA de dos formas: una con los bloques 1, 2 y 3 y otra con los 3, 2 y 1.

Definir la función

soluciones :: [String] -> String -> [[String]]

tal que (soluciones bs cs) es la lista de las soluciones del juego de los bloque usando los bloques bs (cada bloque es una cadena de dos letras mayúsculas) para formar la palabra cs. Por ejemplo,

λ> soluciones ["AB","NO","OA"] "ANA"
[["AB","NO","OA"],["OA","NO","AB"]]
λ> soluciones ["AB","NE","OA"] "Bea"
[["AB","NE","OA"]]
λ> soluciones ["AB","NE","OA"] "EvA"
[]
λ> soluciones ["AB","NO","OA","NC"] "ANA"
[["AB","NO","OA"],["AB","NC","OA"],["OA","NO","AB"],["OA","NC","AB"]]
λ> soluciones ["AB","NO","OA","NC"] "Anca"
[["AB","NO","NC","OA"],["OA","NO","NC","AB"]]
λ> soluciones (["AB","NO","OA"] ++ replicate (10^6) "PQ") "ANA"
[["AB","NO","OA"],["OA","NO","AB"]]

Leer más…

La Enciclopedia electrónica de sucesiones de enteros (OEIS por sus siglas en inglés, de On-Line Encyclopedia of Integer Sequences) es una base de datos que registra sucesiones de números enteros. Está disponible libremente en Internet, en la dirección http://oeis.org.

La semana pasada Antonio Roldán añadió una nueva sucesión a la OEIS, la A249624 que sirve de base para el problema de hoy.

Definir la sucesión

a249624 :: [Integer]

tal que sus elementos son los números x tales que la suma de x y el primo que le sigue es un número primo. Por ejemplo,

λ> take 20 a249624
[0,1,2,6,8,14,18,20,24,30,34,36,38,48,50,54,64,68,78,80]

El número 8 está en la sucesión porque su siguiente primo es 11 y 8+11=19 es primo. El 12 no está en la sucesión porque su siguiente primo es 13 y 12+13=25 no es primo.

Leer más…

El siguiente tipo de dato representa expresiones construidas con variables, sumas y productos

data Expr = Var String
          | S Expr Expr
          | P Expr Expre
          deriving (Eq, Show)

Por ejemplo, x*(y+z) se representa por (P (V "x") (S (V "y") (V "z")))

Una expresión es un término si es un producto de variables. Por ejemplo, x*(y*z) es un término pero x+(y*z) ni x*(y+z) lo son.

Una expresión está en forma normal si es una suma de términos. Por ejemplo, x*(y*z) y x+(y*z) están en forma normal; pero x*(y+z) y (x+y)*(x+z) no lo están.

Definir la función

esTermino :: Expr -> Bool
esTermino :: Expr -> Bool
normal    :: Expr -> Expr

tales que

• (esTermino a) se verifica si a es un término. Por ejemplo,

esTermino (V "x")                         == True
esTermino (P (V "x") (P (V "y") (V "z"))) == True
esTermino (P (V "x") (S (V "y") (V "z"))) == False
esTermino (S (V "x") (P (V "y") (V "z"))) == False

• (esNormal a) se verifica si a está en forma normal. Por ejemplo,

esNormal (V "x")                                     == True
esNormal (P (V "x") (P (V "y") (V "z")))             == True
esNormal (S (V "x") (P (V "y") (V "z")))             == True
esNormal (P (V "x") (S (V "y") (V "z")))             == False
esNormal (P (S (V "x") (V "y")) (S (V "y") (V "z"))) == False
esNormal (S (P (V "x") (V "y")) (S (V "z") (V "x"))) == True

• (normal e) es la forma normal de la expresión e obtenida aplicando, mientras que sea posible, las propiedades distributivas:

(a+b)*c = a*c+b*c
c*(a+b) = c*a+c*b

Por ejemplo,

λ> normal (P (S (V "x") (V "y")) (V "z"))
S (P (V "x") (V "z")) (P (V "y") (V "z"))
λ> normal (P (V "z") (S (V "x") (V "y")))
S (P (V "z") (V "x")) (P (V "z") (V "y"))
λ> normal (P (S (V "x") (V "y")) (S (V "u") (V "v")))
S (S (P (V "x") (V "u")) (P (V "x") (V "v")))
   (S (P (V "y") (V "u")) (P (V "y") (V "v")))
λ> normal (S (P (V "x") (V "y")) (V "z"))
S (P (V "x") (V "y")) (V "z")
λ> normal (V "x")
V "x"

Comprobar con QuickCheck que para cualquier expresión e, (normal e) está en forma normal y que (normal (normal e)) es igual a (normal e).

Nota. Para la comprobación se usará el siguiente generador de expresiones aritméticas

import Test.QuickCheck
import Control.Monad

instance Arbitrary Expr where
  arbitrary = sized arb
    where
      arb 0         = liftM V arbitrary
      arb n | n > 0 = oneof [liftM V arbitrary,
                             liftM2 S sub sub,
                             liftM2 P sub sub]
        where sub = arb (n `div` 2)

Leer más…

Definir la función

sinConsecutivosRepetidos :: Eq a => [a] -> [a]

tal que (sinConsecutivosRepetidos xs) es la lista obtenida a partir de xs de forma que si hay dos o más elementos idénticos consecutivos, borra las repeticiones y deja sólo el primer elemento. Por ejemplo,

λ> sinConsecutivosRepetidos "eesssooo essss   toodddooo"
"eso es todo"

Leer más…

Definir la función

busca :: Eq a => a -> [[(a,b)]] -> [b]

tal que (busca x pss) es la lista de los segundos componentes de los pares de la lista de listas de pares pss cuya primera componentes es x. Por ejemplo,

busca 3 [[(3,4)],[(5,4),(3,2),(3,5)],[(4,1),(7,3)]] == [4,2,5]

Leer más…

Un hotel dispone de n habitaciones y n camareros. Los camareros tienen la costumbre de cambiar de estado las puestas (es decir, abrir las cerradas y cerrar las abiertas). El proceso es el siguiente:

• Inicialmente todas las puertas están cerradas.
• El primer camarero cambia de estado las puertas de todas las habitaciones.
• El segundo cambia de estado de las puertas de las habitaciones pares.
• El tercero cambia de estado todas las puertas que son múltiplos de 3.
• El cuarto cambia de estado todas las puertas que son múltiplos de 4
• Así, hasta que ha pasado el último camarero.

Por ejemplo, para n = 5

Pase    | Puerta 1 | Puerta 2 | Puerta 3 | Puerta 4 | Puerta 5
Inicial | Cerrada  | Cerrada  | Cerrada  | Cerrada  | Cerrada
Pase 1  | Abierta  | Abierta  | Abierta  | Abierta  | Abierta
Pase 2  | Abierta  | Cerrada  | Abierta  | Cerrada  | Abierta
Pase 3  | Abierta  | Cerrada  | Cerrada  | Cerrada  | Abierta
Pase 4  | Abierta  | Cerrada  | Cerrada  | Abierta  | Abierta
Pase 5  | Abierta  | Cerrada  | Cerrada  | Abierta  | Cerrada

Los estados de las puertas se representan por el siguiente tipo de datos

data Estado = Abierta | Cerrada
              deriving (Eq, Show)

Definir la función

final :: Int -> [Estado]

tal que (final n) es la lista de los estados de las n puertas después de que hayan pasado los n camareros. Por ejemplo,

λ> final 5
[Abierta,Cerrada,Cerrada,Abierta,Cerrada]
λ> final 7
[Abierta,Cerrada,Cerrada,Abierta,Cerrada,Cerrada,Cerrada]

Leer más…