Un número de Aquiles es un número natural n que es potente (es decir, si p es un divisor primo de n, entonces p² también lo es) y no es una potencia perfecta (es decir, no existen números naturales m y k tales que n es igual a m^k). Por ejemplo,

• 108 es un número de Aquiles proque es un número potente (ya que su factorización es 2^2 · 3^3, sus divisores primos son 2 and 3 y sus cuadrados (2^2 = 4 y 3^2 = 9) son divisores de 108. Además, 108 no es una potencia perfecta.
• 360 no es un número de Aquiles ya que 5 es un divisor primo de 360, pero 5^2 = 15 no lo es.
• 784 no es un número de Aquiles porque, aunque es potente, es una potencia perfecta ya que 784 = 28^2.

Los primeros números de Aquiles son

72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, ...

Definir las funciones

esAquiles              :: Integer -> Bool
huecosDeAquiles        :: [Integer]
graficaHuecosDeAquiles :: Int -> IO ()

tales que

• (esAquiles x) se verifica si x es un número de Aquiles. Por ejemplo,

esAquiles 108         ==  True
esAquiles 360         ==  False
esAquiles 784         ==  False
esAquiles 5425069447  ==  True
esAquiles 5425069448  ==  True

• huecosDeAquiles es la sucesión de la diferencias entre los números de Aquiles consecutivos. Por ejemplo,

λ> take 15 huecosDeAquiles
[36,92,88,104,40,68,148,27,125,64,104,4,153,27,171]

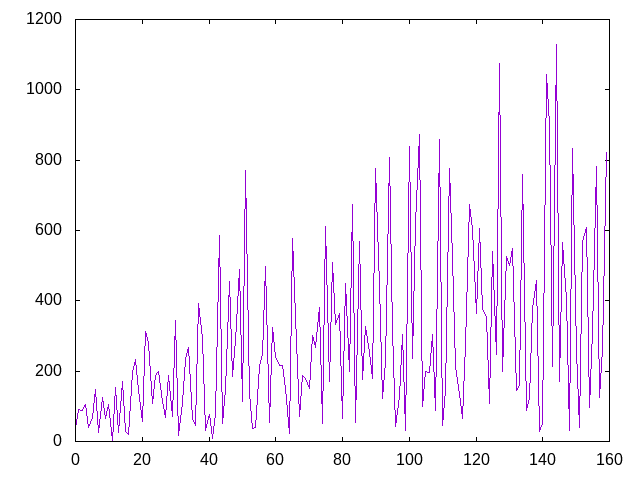
• (graficaHuecosDeAquiles n) dibuja la gráfica de los n primeros huecos de Aquiles. Por ejemplo, (graficaHuecosDeAquiles 160) dibuja

Leer más…

Definir las funciones

minimasDistancias             :: Matrix Int -> Matrix Int
sumaMinimaDistanciasIdentidad :: Int -> Int

tales que

• (mininasDistancias a) es la matriz de las mínimas distancias de cada elemento de a hasta alcanzar un 1 donde un paso es un movimiento hacia la izquierda, derecha, arriba o abajo. Por ejemplo,

λ> minimasDistancias (fromLists [[0,1,1],[0,0,1]])
( 1 0 0 )
( 2 1 0 )
λ> minimasDistancias (fromLists [[0,0,1],[1,0,0]])
( 1 1 0 )
( 0 1 1 )
λ> minimasDistancias (identity 5)
( 0 1 2 3 4 )
( 1 0 1 2 3 )
( 2 1 0 1 2 )
( 3 2 1 0 1 )
( 4 3 2 1 0 )

• (sumaMinimaDistanciasIdentidad n) es la suma de los elementos de la matriz de las mínimas distancias correspondiente a la matriz identidad de orden n. Por ejemplo,

sumaMinimaDistanciasIdentidad 5       ==  40
sumaMinimaDistanciasIdentidad (10^2)  ==  333300
sumaMinimaDistanciasIdentidad (10^4)  ==  333333330000
sumaMinimaDistanciasIdentidad (10^6)  ==  333333333333000000

Leer más…

Definir la función

tieneCombinacionDivisible :: [Int] -> Int -> Bool

tal que (tieneCombinacionDivisible xs m) se verifica si existe alguna forma de combinar todos los elementos de la lista (con las operaciones suma o resta) de forma que el resultado sea divisible por m. Por ejemplo,

tieneCombinacionDivisible [1,3,4,6] 4  ==  True
tieneCombinacionDivisible [1,3,9]   2  ==  False

En el primer ejemplo, 1 - 2 + 3 + 4 + 6 = 12 es una combinación divisible por 4. En el segundo ejemplo, las combinaciones de [1,3,9] son

 1 + 3 + 9 =  13
-1 + 3 + 9 =  11
 1 - 3 + 9 =   7
-1 - 3 + 9 =   5
 1 + 3 - 9 =  -5
-1 + 3 - 9 =  -7
 1 - 3 - 9 = -11
-1 - 3 - 9 = -13

y ninguna de las 4 es divisible por 2.

Leer más…

Los segmentos iniciales de [3,1,2,5] son [3], [3,1], [3,1,2] y [3,1,2,5]. Sus sumas son 3, 4, 6 y 9, respectivamente. La suma de dichas sumas es 24.

Definir la función

sumaSegmentosIniciales :: [Integer] -> Integer

tal que (sumaSegmentosIniciales xs) es la suma de las sumas de los segmentos iniciales de xs. Por ejemplo,

sumaSegmentosIniciales [3,1,2,5]     ==  24
sumaSegmentosIniciales3 [1..3*10^6]  ==  4500004500001000000

Comprobar con QuickCheck que la suma de las sumas de los segmentos iniciales de la lista formada por n veces el número uno es el n-ésimo número triangular; es decir que

sumaSegmentosIniciales (genericReplicate n 1)

es igual a

n * (n + 1) `div` 2

Leer más…

Los árboles se pueden representar mediante el siguiente tipo de datos

   data Arbol = N Int [Arbol]
     deriving Show

Por ejemplo, los árboles

     1             1             1
    /  \          / \           / \
   /    \        8   3         8   3
  2      6          /|\       /|\  |
 / \    / \        4 2 6     4 5 6 2
4   5  5   7

se representan por

ej1, ej2, ej3 :: Arbol
ej1 = N 1 [N 2 [N 4 [], N 5 []], N 6 [N 5 [], N 7 []]]
ej2 = N 1 [N 8 [], N 3 [N 4 [], N 2 [], N 6 []]]
ej3 = N 1 [N 8 [N 4 [], N 5 [], N 6 []], N 3 [N 2 []]]

Definir la función

hojasEnNoDecreciente :: Arbol -> [Int]

tal que (hojasEnNoDecreciente a) es el conjunto de las hojas de a que se encuentran en alguna rama no decreciente. Por ejemplo,

hojasEnNoDecreciente ej1  ==  [4,5,7]
hojasEnNoDecreciente ej2  ==  [4,6,8]
hojasEnNoDecreciente ej3  ==  []

Leer más…

Las matrices de Hadamard se definen recursivamente como sigue

λ> hadamard 0
( 1 )

λ> hadamard 1
(  1  1 )
(  1 -1 )

λ> hadamard 2
(  1  1  1  1 )
(  1 -1  1 -1 )
(  1  1 -1 -1 )
(  1 -1 -1  1 )

λ> hadamard 3
(  1  1  1  1  1  1  1  1 )
(  1 -1  1 -1  1 -1  1 -1 )
(  1  1 -1 -1  1  1 -1 -1 )
(  1 -1 -1  1  1 -1 -1  1 )
(  1  1  1  1 -1 -1 -1 -1 )
(  1 -1  1 -1 -1  1 -1  1 )
(  1  1 -1 -1 -1 -1  1  1 )
(  1 -1 -1  1 -1  1  1 -1 )

En general, la n-ésima matriz de Hadamard, H(n), es

( H(n-1)  H(n-1) )
( H(n-1) -H(n-1) )

Definir la función

hadamard :: Int -> Matrix Int

tal que (hadamard n) es la n-ésima matriz de Hadamard.

Comprobar con QuickCheck que para todo número natural n, el producto de la n-ésima matriz de Hadamard y su traspuesta es igual al producto de 2^n por la matriz identidad de orden 2^n.

Leer más…

Definir la función

menorNoSuma :: [Integer] -> Integer

tal que (menorNoSuma xs) es el menor número que no se puede escribir como suma de un subconjunto de xs, donde se supone que xs es un conjunto de números enteros positivos. Por ejemplo,

menorNoSuma [6,1,2]    ==  4
menorNoSuma [1,2,3,9]  ==  7
menorNoSuma [5]        ==  1
menorNoSuma [1..20]    ==  211
menorNoSuma [1..10^6]  ==  500000500001

Comprobar con QuickCheck que para todo n,

menorNoSuma [1..n] == 1 + sum [1..n]

Leer más…

El orden de divisibilidad de un número x es el mayor n tal que para todo i menor o igual que n, los i primeros dígitos de n es divisible por i. Por ejemplo, el orden de divisibilidad de 74156 es 3 porque

7       es divisible por 1
74      es divisible por 2
741     es divisible por 3
7415 no es divisible por 4

Definir la función

ordenDeDivisibilidad :: Integer -> Int

tal que (ordenDeDivisibilidad x) es el orden de divisibilidad de x. Por ejemplo,

ordenDeDivisibilidad 74156                      ==  3
ordenDeDivisibilidad 3608528850368400786036725  ==  25

Leer más…

Una progresión aritmética es una sucesión de números tales que la diferencia de dos términos sucesivos cualesquiera de la sucesión es constante.

Definir la función

ausente :: Integral a => [a] -> a

tal que (ausente xs) es el único término ausente de la progresión aritmética xs. Por ejemplo,

ausente [3,7,9,11]               ==  5
ausente [3,5,9,11]               ==  7
ausente [3,5,7,11]               ==  9
ausente ([1..9]++[11..])         ==  10
ausente ([1..10^6] ++ [2+10^6])  ==  1000001

Nota. Se supone que la lista tiene al menos 3 elementos, que puede ser infinita y que sólo hay un término de la progresión aritmética que no está en la lista.

Leer más…

En 1999, L.J. Lange publicó el artículo An elegant new continued fraction for π.

En el primer teorema del artículo se demuestra la siguiente expresión de π mediante una fracción continua

La primeras aproximaciones son

a(1) = 3+1                = 4.0
a(2) = 3+(1/(6+9))        = 3.066666666666667
a(3) = 3+(1/(6+9/(6+25))) = 3.158974358974359

Definir las funciones

aproximacionPi :: Int -> Double
grafica        :: [Int] -> IO ()

tales que

• (aproximacionPi n) es la n-ésima aproximación de pi con la fracción continua de Lange. Por ejemplo,

aproximacionPi 1     ==  4.0
aproximacionPi 2     ==  3.066666666666667
aproximacionPi 3     ==  3.158974358974359
aproximacionPi 10    ==  3.141287132741557
aproximacionPi 100   ==  3.141592398533554
aproximacionPi 1000  ==  3.1415926533392926

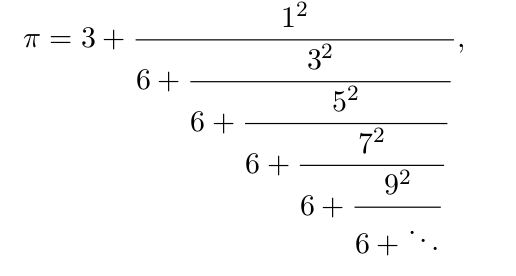
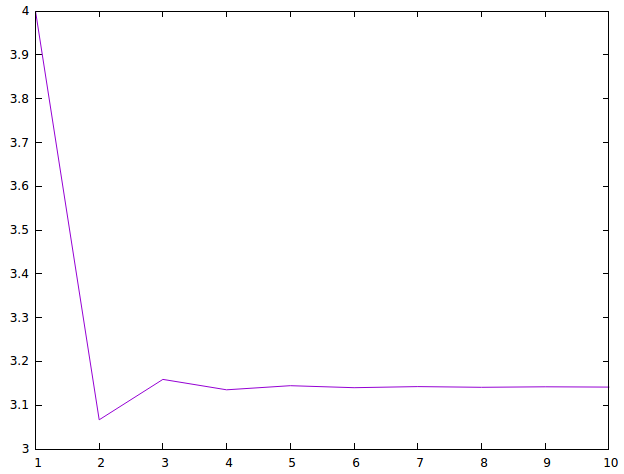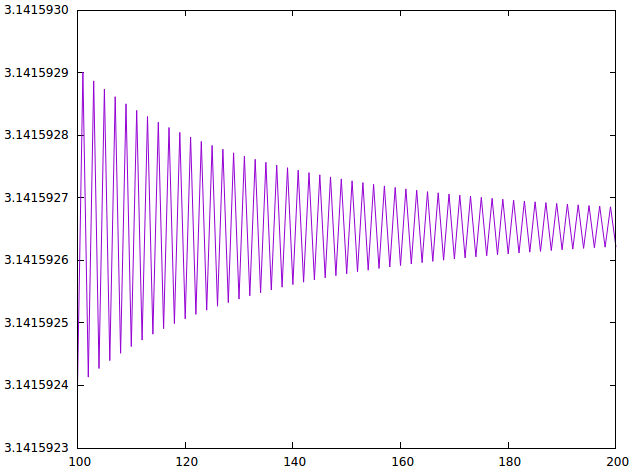
• (grafica xs) dibuja la gráfica de las k-ésimas aproximaciones de pi donde k toma los valores de la lista xs. Por ejemplo, (grafica [1..10]) dibuja (grafica [10..100]) dibuja 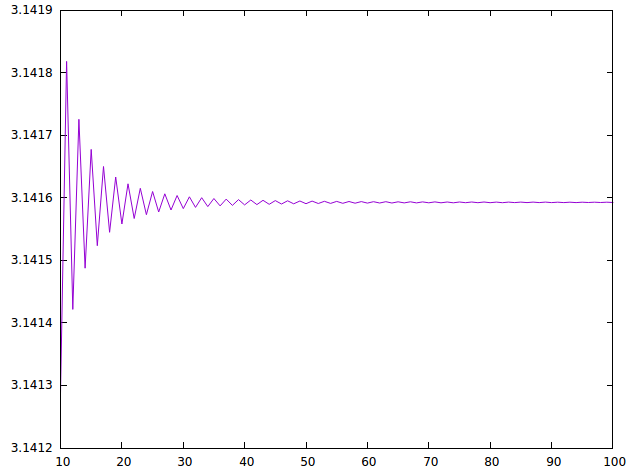y (grafica [100..200]) dibuja

Leer más…