La matriz zizagueante de orden n es la matriz cuadrada con n filas y n columnas y cuyos elementos son los n² primeros números naturales colocados de manera creciente a lo largo de las diagonales secundarias. Por ejemplo, La matriz zigzagueante de orden 5 es

 0  1  5  6 14
 2  4  7 13 15
 3  8 12 16 21
 9 11 17 20 22
10 18 19 23 24

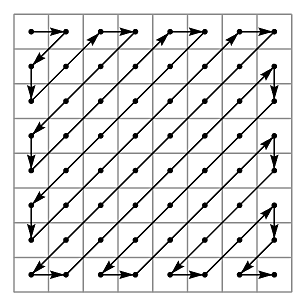
La colocación de los elementos se puede ver gráficamente en Matriz zigzagueante

Definir la función

zigZag :: Int -> Matrix Int

tal que (zigZag n) es la matriz zigzagueante de orden n. Por ejemplo,

λ> zigZag 5
┌                ┐
│  0  1  5  6 14 │
│  2  4  7 13 15 │
│  3  8 12 16 21 │
│  9 11 17 20 22 │
│ 10 18 19 23 24 │
└                ┘
λ> zigZag 4
┌             ┐
│  0  1  5  6 │
│  2  4  7 12 │
│  3  8 11 13 │
│  9 10 14 15 │
└             ┘
λ> maximum (zigZag 1500)
2249999

Soluciones

import Data.List (sort, sortBy)
import Data.Matrix (Matrix, fromList, matrix, toLists)
import Test.Hspec (Spec, describe, hspec, it, shouldBe)
import Test.QuickCheck

-- 1ª solución: Basada en la simulación del recorrido
-- ==================================================

zigZag1 :: Int -> Matrix Int
zigZag1 n = fromList n n (elementosZigZag n)

-- (elementosZigZag n) es la lista de los elementos de la matriz
-- zizagueante de orden n. Por ejemplo.
--    λ> elementosZigZag 5
--    [0,1,5,6,14,2,4,7,13,15,3,8,12,16,21,9,11,17,20,22,10,18,19,23,24]
elementosZigZag :: Int -> [Int]
elementosZigZag n =
  map snd (sort (zip (ordenZigZag n) [0..]))

-- (ordenZigZag n) es la lista de puntos del cuadrado nxn recorridos en
-- zig-zag por las diagonales secundarias. Por ejemplo,
--    λ> ordenZigZag 4
--    [(1,1), (1,2),(2,1), (3,1),(2,2),(1,3), (1,4),(2,3),(3,2),(4,1),
--     (4,2),(3,3),(2,4), (3,4),(4,3), (4,4)]
ordenZigZag :: Int -> [(Int,Int)]
ordenZigZag n = concat [aux n m | m <- [2..2*n]]
  where aux k m | odd m     = [(x,m-x) | x <- [max 1 (m-k)..min k (m-1)]]
                | otherwise = [(m-x,x) | x <- [max 1 (m-k)..min k (m-1)]]

-- 2ª solución: Basada en propiedades de ordenación
-- ================================================

zigZag2 :: Int -> Matrix Int
zigZag2 n = fromList n n (elementosZigZag2 n)

elementosZigZag2 :: Int -> [Int]
elementosZigZag2 n =
  map snd (sort (zip (ordenZigZag2 n) [0..]))

ordenZigZag2 :: Int -> [(Int,Int)]
ordenZigZag2 n = sortBy comp [(x,y) | x <- [1..n], y <- [1..n]]
  where comp (x1,y1) (x2,y2) | x1+y1 < x2+y2 = LT
                             | x1+y1 > x2+y2 = GT
                             | even (x1+y1)  = compare y1 y2
                             | otherwise     = compare x1 x2

-- 3ª solución: Basada en cálculo analítico y función matrix
-- =========================================================

zigZag3 :: Int -> Matrix Int
zigZag3 n = matrix n n f
  where
    f (r, c) =
      let -- Convertimos a índices 0-based para simplificar los cálculos
          i = r - 1
          j = c - 1
          s = i + j
          -- Elementos en las diagonales anteriores a 's'
          area | s < n     = (s * (s + 1)) `div` 2
               | otherwise = n * n - ((2 * n - 1 - s) * (2 * n - s)) `div` 2
          -- Límites del índice de fila 'i' en la diagonal actual
          iMin = max 0 (s - n + 1)
          iMax = min s (n - 1)
      in if even s
         then area + (iMax - i) -- Zigzag hacia arriba (i decrece)
         else area + (i - iMin) -- Zagzag hacia abajo (i crece)

-- 4ª solución: Basada en cálculo analítico y fromList
-- ===================================================

zigZag4 :: Int -> Matrix Int
zigZag4 n = fromList n n [calcula i j | i <- [0..n-1], j <- [0..n-1]]
  where
    -- Función de conveniencia para números triangulares
    triangular k = (k * (k + 1)) `quot` 2
    calcula i j =
      let s = i + j
          -- Área: suma de elementos en las diagonales anteriores
          area | s < n     = triangular s
               | otherwise = n * n - triangular (2 * n - 1 - s)
          -- Límites de la fila i para la diagonal s
          iMin = max 0 (s - n + 1)
          iMax = min s (n - 1)
      in if even s
         then area + (iMax - i) -- En diagonales pares, sube (i disminuye)
         else area + (i - iMin) -- En diagonales impares, baja (i aumenta)

-- Verificación
-- ============

verifica :: IO ()
verifica = hspec spec

specG :: (Int -> Matrix Int) -> Spec
specG zigZag = do
  it "e1" $
    toLists (zigZag 5) `shouldBe`
    [[0,1,5,6,14],[2,4,7,13,15],[3,8,12,16,21],[9,11,17,20,22],[10,18,19,23,24]]
  it "e2" $
    toLists (zigZag 4) `shouldBe`
    [[0,1,5,6],[2,4,7,12],[3,8,11,13],[9,10,14,15]]

spec :: Spec
spec = do
  describe "def. 1" $ specG zigZag1
  describe "def. 2" $ specG zigZag2
  describe "def. 3" $ specG zigZag3
  describe "def. 4" $ specG zigZag4

-- La verificación es
--    λ> verifica
--    6 examples, 0 failures

-- Comprobación de equivalencia
-- ============================

-- La propiedad es
prop_equivalencia :: Positive Int -> Bool
prop_equivalencia (Positive n) =
  all (== zigZag1 n)
      [ zigZag2 n
      , zigZag3 n
      , zigZag4 n
      ]

-- La comprobación es
--    λ> quickCheck prop_equivalencia
--    +++ OK, passed 100 tests.

-- Comparación de eficiencia
-- =========================

-- La comparación es
--    λ> maximum (zigZag1 1100)
--    1209999
--    (2.70 secs, 1,858,516,928 bytes)
--    λ> maximum (zigZag2 1100)
--    1209999
--    (21.73 secs, 11,807,246,336 bytes)
--    λ> maximum (zigZag3 1100)
--    1209999
--    (3.28 secs, 1,839,600,792 bytes)
--    λ> maximum (zigZag4 1100)
--    1209999
--    (3.99 secs, 2,091,650,568 bytes)