Tema 13: Programas interactivos

juego :: IO ()
juego = do
  putStrLn "Piensa un numero entre el 1 y el 100."
  adivina 1 100
  putStrLn "Fin del juego"

adivina :: Int -> Int -> IO ()
adivina a b = do
  putStr ("Es " ++ show conjetura ++ "? [mayor/menor/exacto] ")
  s <- getLine
  case s of
    "mayor"  -> adivina (conjetura+1) b
    "menor"  -> adivina a (conjetura-1)
    "exacto" -> return ()
    _        -> adivina a b
    where
      conjetura = (a+b) `div` 2

import System.Random (randomRIO)

juego2 :: IO ()
juego2 = do n <- randomRIO (1::Int,100)
            putStrLn "Tienes que adivinar un numero entre 1 y 100"
            adivina' n

adivina' :: Int -> IO ()
adivina' n =
    do putStr "Escribe un numero: "
       c <- getLine
       let x = read c
       case (compare x n) of
         LT -> do putStrLn " es bajo."
                  adivina' n
         GT -> do putStrLn " es alto."
                  adivina' n
         EQ -> putStrLn " Exactamente"

import I1M.Analizador
import System.IO

getCh :: IO Char
getCh = do hSetEcho stdin False
           c <- getChar
           hSetEcho stdin True
           return c

limpiaPantalla :: IO ()
limpiaPantalla = putStr "\ESC[2J"

type Pos = (Int,Int)

irA :: Pos -> IO ()
irA (x,y) = putStr ("\ESC[" ++
                    show y ++ ";" ++ show x ++
                    "H")

escribeEn :: Pos -> String -> IO ()
escribeEn p xs = do irA p
                    putStr xs

calculadora :: IO ()
calculadora = do limpiaPantalla
                  escribeCalculadora
                limpiar

escribeCalculadora :: IO ()
escribeCalculadora =
 do limpiaPantalla
    sequence_ [escribeEn (1,y) xs
               | (y,xs) <- zip [1..13] imagenCalculadora]
    putStrLn ""

imagenCalculadora :: [String]
imagenCalculadora = ["+---------------+",
                     "|               |",
                     "+---+---+---+---+",
                     "| q | c | d | = |",
                     "+---+---+---+---+",
                     "| 1 | 2 | 3 | + |",
                     "+---+---+---+---+",
                     "| 4 | 5 | 6 | - |",
                     "+---+---+---+---+",
                     "| 7 | 8 | 9 | * |",
                     "+---+---+---+---+",
                     "| 0 | ( | ) | / |",
                     "+---+---+---+---+"]

limpiar :: IO ()
limpiar = calc ""

calc :: String -> IO ()
calc xs = do escribeEnPantalla xs
             c <- getCh
             if elem c botones
                then procesa c xs
                else calc xs

escribeEnPantalla xs =
    do escribeEn (3,2) "             "
       escribeEn (3,2) (reverse (take 13 (reverse xs)))

botones :: String
botones = standard ++ extra
    where
      standard = "qcd=123+456-789*0()/"
      extra    = "QCD \ESC\BS\DEL\n"

procesa :: Char -> String -> IO ()
procesa c xs
   | elem c "qQ\ESC"    = salir
   | elem c "dD\BS\DEL" = borrar xs
   | elem c "=\n"       = evaluar xs
   | elem c "cC"        = limpiar
   | otherwise          = agregar c xs

salir :: IO ()
salir = irA (1,14)

borrar :: String -> IO ()
borrar "" = calc ""
borrar xs = calc (init xs)

evaluar :: String -> IO ()
evaluar xs = case analiza expr xs of
             [(n,"")] -> calc (show n)
             _        -> calc xs

agregar :: Char -> String -> IO ()
agregar c xs = calc (xs ++ [c])

cabal install gnuplot

import Graphics.Gnuplot.Simple

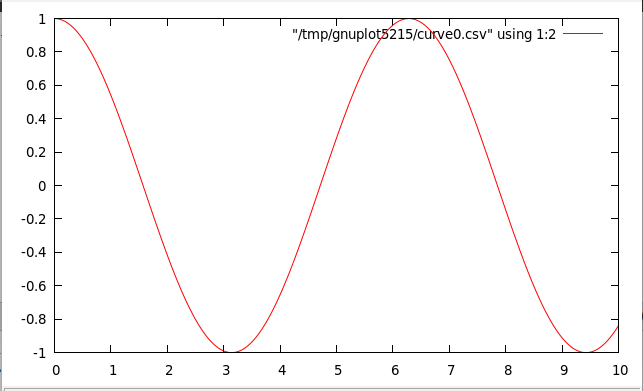
dib0 :: IO ()
dib0 = plotFunc [] [0,0.01..10 :: Double] cos

xRango :: Integer -> (Double,Double) -> [Double]
xRango n i = linearScale n i

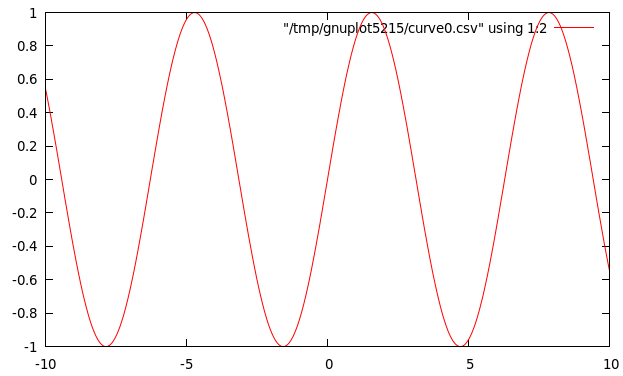
dib1a =
    plotFunc [EPS "ej.eps"] (xRango 500 (-10,10)) sin

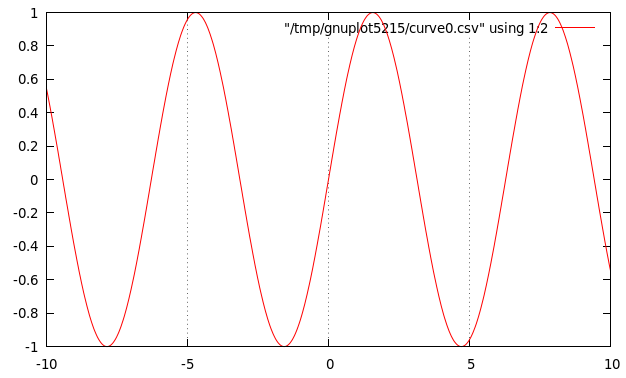
dib1b =
    plotFunc [Grid (Just ["x"])] (xRango 500 (-10,10)) sin

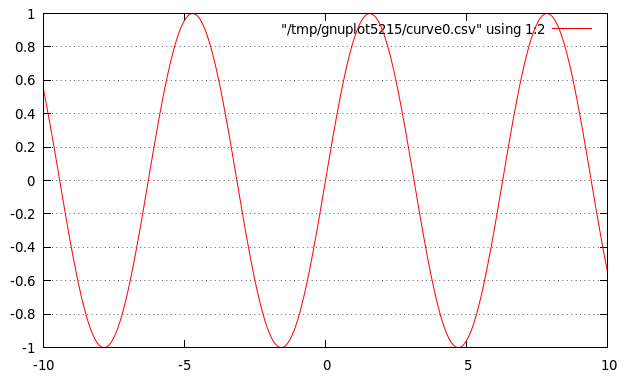
dib1c =
    plotFunc [Grid (Just ["y"])] (xRango 500 (-10,10)) sin

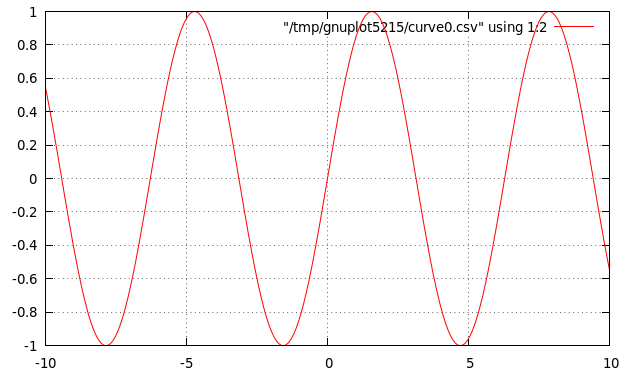
dib1d =
    plotFunc [Grid (Just [])] (xRango 500 (-10,10)) sin

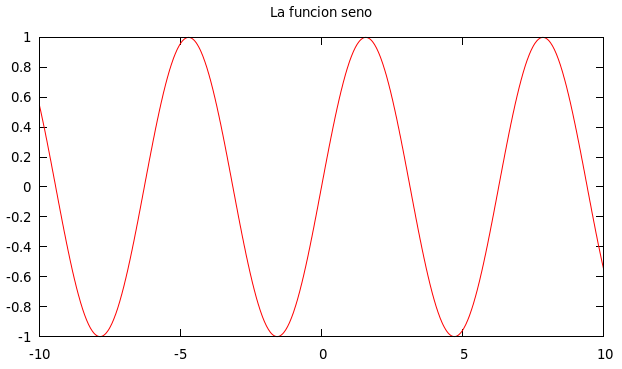
dib1e =
    plotFunc [Title "La funcion seno", Key Nothing]
             (xRango 1000 (-10,10)) sin

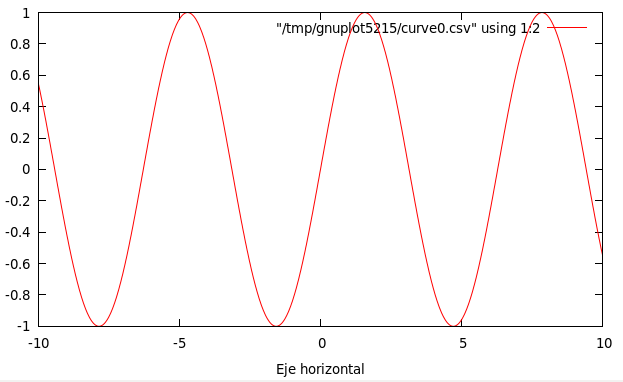
dib1f =
    plotFunc [XLabel "Eje horizontal"] (xRango 1000 (-10,10)) sin

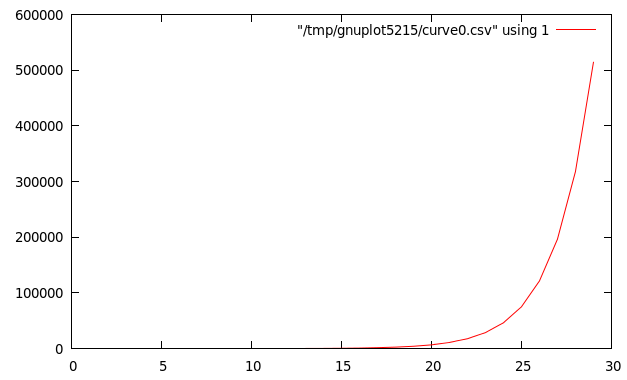
dib2 =
    plotList [] (take 30 fibs)
    where fibs :: [Double]
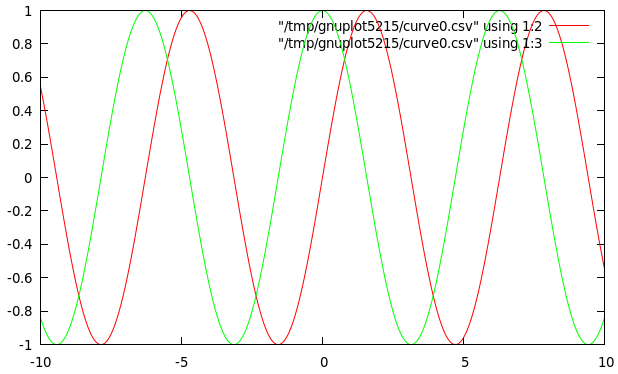
          fibs = 0 : 1 : zipWith (+) fibs (tail fibs)

dib3 =
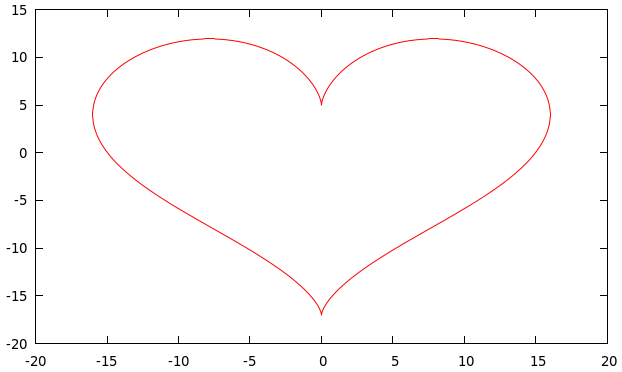
    plotFuncs [] (xRango 1000 (-10,10)) [sin, cos]

dib4 =
    plotParamFunc [Key Nothing]
                  (xRango 1000 (0,2*pi))
                  (\t -> (12*sin(t)-4*sin(3*t),
                          13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t)))

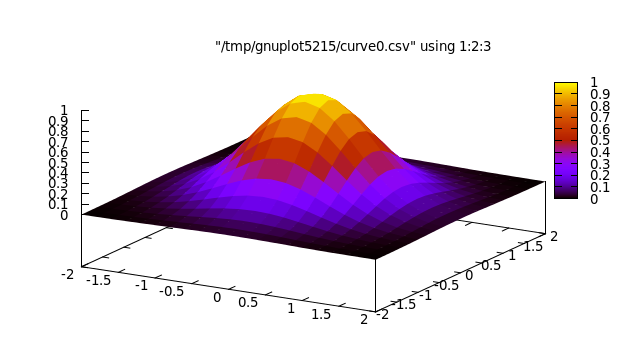
dib5 =
    plotFunc3d [] [] xs xs (\x y -> exp(-(x*x+y*y)))
    where xs = [-2,-1.8..2::Double]

muestraContenidoFichero :: FilePath -> IO ()
muestraContenidoFichero f = do
  cs <- readFile f
  putStrLn cs

import Data.Char (toUpper)

aMayuscula f1 f2 = do
  contenido <- readFile f1
  writeFile f2 (map toUpper contenido)

import Data.List (sort)

ordenaFichero :: FilePath -> FilePath -> IO ()
ordenaFichero f1 f2 = do
  cs <- readFile f1
  writeFile f2 ((unlines . sort . lines) cs)

tablaCuadrados :: FilePath -> Int -> IO ()
tablaCuadrados f n =
  writeFile f (listaDeCuadrados n)

listaDeCuadrados :: Int -> String
listaDeCuadrados n =
  unwords (map show [(x,x*x) | x <- [1..n]])

tablaCuadrados2 :: FilePath -> Int -> IO ()
tablaCuadrados2 f n =
  writeFile f (listaDeCuadrados2 n)

listaDeCuadrados2 :: Int -> String
listaDeCuadrados2 n =
  unlines (map show [(x,x*x) | x <- [1..n]])

import Text.Printf

tablaLogaritmos :: FilePath -> [Int] -> IO ()
tablaLogaritmos f ns = do
  writeFile f (tablaLogaritmosAux ns)

tablaLogaritmosAux :: [Int] -> String
tablaLogaritmosAux ns =
     linea
  ++ cabecera
  ++ linea
  ++ concat [printf "| %2d | %.12f |\n" n x
            | n <- ns
            , let x = log (fromIntegral n) :: Double]
  ++ linea

linea, cabecera :: String
linea    = "+----+----------------+\n"
cabecera = "| n  | log(n)         |\n"