Tema 24: Programación dinámica

Definición de Fibonacci por divide y vencerás.

fib 0 = 0
fib 1 = 1
fib n = fib (n-1) + fib (n-2)

Cálculo de (fib 4) por divide y vencerás

                      fib 4
                     /     \
              +-----+       +--+
              |                |
            fib 3             fib 2
           /     \           /     \
      fib 2       fib 1 fib 1       fib 0
     /     \
fib 1       fib 0

Calcula 2 veces (fib 2) y 3 veces (fib 1) y (fib 0).</p>

Cálculo de (fib 4) por programación dinámica

fib 0
 |    fib 1
 |     |
 +-----+=== fib 2
       |     |
       +-----+=== fib 3
             |     |
             +-----+=== fib 4

Cabecera del módulo:

module Dinamica (module Tabla, dinamica)  where

Librerías auxiliares

-- Hay que elegir una implementación de TAD Tabla
-- import TablaConFunciones as Tabla
import TablaConListasDeAsociacion as Tabla
-- import TablaConMatrices as Tabla

import Data.Array

El patrón de la programación dinámica

dinamica :: Ix i => (Tabla i v -> i -> v) -> (i,i) -> Tabla i v
dinamica calcula cotas = t
  where t = tabla [(i,calcula t i) | i <- range cotas]

• (calcula t i) es el valor del índice i calculado a partir de los anteriores que ya se encuentran en la tabla t.
• cotas son las cotas de la matriz t en la que se almacenan los valores calculados.

Importación del patrón de programación dinámica

import Dinamica

(fib n) es el n-ésimo término de la sucesión de Fibonacci, calculado mediante programación dinámica. Por ejemplo,

fib 8  ==  21

Su definición es

fib :: Int -> Int
fib n = valor t n
  where t = dinamica calculaFib (cotasFib n)

(calculaFib t i) es el valor de i-ésimo término de la sucesión de Fibonacci calculado mediante la tabla t que contiene los anteriores. Por ejemplo,

calculaFib (tabla []) 0                       == 0
calculaFib (tabla [(0,0),(1,1),(2,1),(3,2)] 4 == 3

Además,

λ> dinamica calculaFib (0,6)
Tbl [(0,0),(1,1),(2,1),(3,2),(4,3),(5,5),(6,8)]

Su definición es

calculaFib :: Tabla Int Int -> Int -> Int
calculaFib t i
 | i <= 1    = i
 | otherwise = valor t (i-1) + valor t (i-2)

(cotasFib n) son las cotas del vector que se necesita para calcular el n-ésimo término de la sucesión de Fibonacci mediante programación dinámica.

cotasFib :: Int -> (Int,Int)
cotasFib n = (0,n)

(fibR n) es el n-ésimo término de la sucesión de Fibonacci calculado mediante divide y vencerás.

fibR :: Int -> Int
fibR 0 = 0
fibR 1 = 1
fibR n = fibR (n-1) + fibR (n-2)

Comparación:

λ> fib 30
832040
(0.01 secs, 0 bytes)
λ> fibR 30
832040
(6.46 secs, 222602404 bytes)

fibs es la lista de los términos de la sucesión de Fibonacci. Por ejemplo,

take 10 fibs  ==  [0,1,1,2,3,5,8,13,21,34]

Su definición es

fibs :: [Int]
fibs = 0:1:[x+y | (x,y) <- zip fibs (tail fibs)]

(fib' n) es el n-ésimo término de la sucesión de Fibonacci, calculado a partir de fibs. Por ejemplo,

fib' 8  ==  21

Su definición es

fib' :: Int -> Int
fib' n = fibs!!n

Comparaciones:

λ> fib 30
832040
(0.02 secs, 524808 bytes)
λ> fib' 30
832040
(0.01 secs, 542384 bytes)
λ> fibR 30
832040
(6.46 secs, 222602404 bytes)

Ejemplo: Dada la sucesión de matrices

A (30 x 1), B (1 x 40), C (40 x 10), D (10 x 25)

las productos necesarios en las posibles asociaciones son

((AB)C)D  30 x  1 x 40 + 30 x 40 x 10 + 30 x 10 x 25 = 20700
A(B(CD))  40 x 10 x 25 +  1 x 40 x 25 + 30 x  1 x 25 = 11750
(AB)(CD)  30 x  1 x 40 + 40 x 10 x 25 + 30 x 40 x 25 = 41200
A((BC)D)   1 x 40 x 10 +  1 x 10 x 25 + 30 x  1 x 25 =  1400
(A(BC))D   1 x 40 x 10 + 30 x  1 x 10 + 30 x 10 x 25 =  8200

Relación de recurrencia de c(i,j):

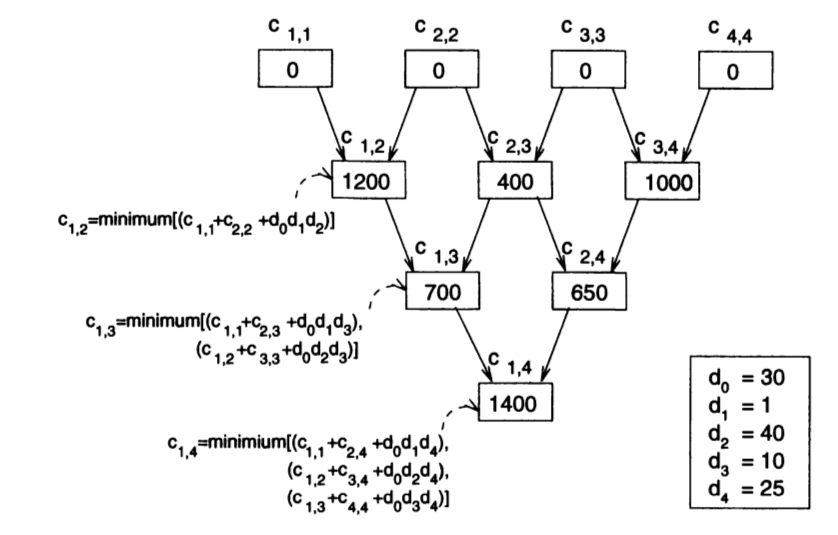
c(i,i) = 0
c(i,j) = minimo {c(i,k)+c(k+1,j)+d(i-1)*d(k)*d(j) | i ≤ k < j}

Importación de librerías auxiliares:

import Dinamica

Cadena representa el producto de una cadena de matrices. Por ejemplo,

P (A 1) (P (A 2) (A 3))  ==  (A1*(A2*A3))
P (P (A 1) (A 2)) (A 3)  ==  ((A1*A2)*A3)

Su definición es

data Cadena = A Int
            | P Cadena Cadena

instance Show Cadena where
  show (A x)     = "A" ++ show x
  show (P p1 p2) = concat ["(",show p1,"*",show p2,")"]

Los índices de la matriz de cálculo son de la forma (i,j) y sus valores (v,k) donde v es el mínimo número de multiplicaciones necesarias para multiplicar la cadena A(i), …,A(j) y k es la posición donde dividir la cadena de forma óptima.

type IndicePCM = (Int,Int)
type ValorPCM  = (Int,Int)

(pcm ds) es el par formado por el mínimo número de multiplicaciones elementales para multiplicar una sucesión de matrices A(1), …, A(n) (tal que el orden de A(i) es d(i-1) x d(i) y ds = [d(0), …,d(n)]). Por ejemplo,

pcm [30,1,40,10,25]  == (1400,(A1*((A2*A3)*A4)))

Su definición es

pcm :: [Int] -> (Int, Cadena)
pcm ds = (v, cadena t 1 n)
  where n     = length ds - 1
        t     = dinamica (calculaPCM ds) (cotasPCM n)
        (v,_) = valor t (1,n)

(calculaPCM ds t (i,j)) es el valor del índice (i,j) calculado a partir de la lista ds de dimensiones de las matrices y la tabla t de valores previamente calculados.

calculaPCM :: [Int] -> Tabla IndicePCM ValorPCM
              -> IndicePCM -> ValorPCM
calculaPCM ds t (i,j)
    | i == j    = (0,i)
    | otherwise =
         minimum [(fst(valor t (i,k))
                  + fst(valor t (k+1,j))
                  + ds!!(i-1) * ds!!k * ds!!j, k)
                  | k <- [i..j-1]]

(cotasPCM n) son las cotas de los índices para el producto de una cadena de n matrices.

cotasPCM :: Int -> (IndicePCM,IndicePCM)
cotasPCM n = ((1,1),(n,n))

(cadena t i j) es la cadena que resultar de agrupar las matrices A(i), …, A(j) según los valores de la tabla t.

cadena :: Tabla IndicePCM ValorPCM -> Int -> Int -> Cadena
cadena t i j
    | i == j-1  = P (A i) (A j)
    | k == i    = P (A i) (cadena t (i+1) j)
    | k == j-1  = P (cadena t i (j-1)) (A j)
    | otherwise = P (cadena t i (k-1)) (cadena t k j)
    where (_,k) = valor t (i,j)

(pcm' ds) es la lista de los índices y valores usados en el cálculo del mínimo número de multiplicaciones necesarias para multiplicar una sucesión de matrices A(1), …,A(n) (tal que el orden de A(i) es d(i-1) x d(i) y ds = [d(0), …, d(n)]). Por ejemplo,

λ> pcm' [30,1,40,10,25]
[((1,1),(0,1)),((1,2),(1200,1)),((1,3),(700,1)),((1,4),(1400,1)),
 ((2,2),(0,2)),((2,3),(400,2)),((2,4),(650,3)),
 ((3,3),(0,3)),((3,4),(10000,3)),
 ((4,4),(0,4))]

Su definición es

pcm' :: [Int] -> [((Int, Int), ValorPCM)]
pcm' ds = [((i,j),valor t (i,j)) | i <- [1..n], j <- [i..n]]
    where n = length ds - 1
          t = dinamica (calculaPCM ds) (cotasPCM n)

(pcmDyV ds) es la solución del PCM correspondiente a ds mediante divide y vencerás. Por ejemplo,

pcmDyV [30,1,40,10,25]  ==  (1040,(A1*((A2*A3)*A4)))

Su definición es

pcmDyV :: [Int] -> (Int, Cadena)
pcmDyV ds = cadenaDyV ds 1 n
  where n = length ds - 1

cadenaDyV ds i j) es la solución del PCM correspondiente a [d(i), …, d(j)]. Por ejemplo,

cadenaDyV [30,1,40,10,25] 1 4  ==  (1040,(A1*((A2*A3)*A4)))
cadenaDyV [30,1,40,10,25] 2 4  ==  (650,((A2*A3)*A4))

Su definición es

cadenaDyV :: [Int] -> Int -> Int -> (Int, Cadena)
cadenaDyV ds i j
  | i == j    = (0, A i)
  | i == j-1  = (ds!!(i-1)*ds!!i*ds!!j, P (A i) (A j))
  | k == i    = (v, P (A i) (subcadena (i+1) j))
  | k == j-1  = (v, P (subcadena i (j-1)) (A j))
  | otherwise = (v, P (subcadena i (k-1)) (subcadena k j))
  where (v,k) = minimum [((valor i k)
                          + (valor (k+1) j)
                          + ds!!(i-1) * ds!!k * ds!!j, k)
                         | k <- [i..j-1]]
        valor p q     = fst (cadenaDyV ds p q)
        subcadena p q = snd (cadenaDyV ds p q)

Comparación de las métodos de solucionar el PCM

λ> :set +s

λ> fst (pcm [1..20])
2658
(0.04 secs, 4144552 bytes)

λ> fst (pcmDyV [1..20])
2658
(1582.60 secs, 340414297896 bytes)

• c(i,j) es el mínimo coste del camino del vértice i al j.
• p(i,j) =
  • 0, si i = j
  • peso del arco entre i y j, si i ≠ j y hay arco de i a j
  • ∞, en otro caso
• c(i,j,k) es el mínimo coste del camino del vértice i al j, usando los vértices 1, …,k.

• c(i,j,0) = p(i,j)
• c(i,j,k) = min {c(i,j,k-1)), c(i,k,k-1)+c(k,j,k-1)}

Importación de librerías auxiliares:

import Dinamica

-- Nota: Elegir una implementación de los grafos.
import GrafoConVectorDeAdyacencia
-- import GrafoConMatrizDeAdyacencia

Ejemplos de grafos para el problema:

ej1Grafo :: Grafo Int Int
ej1Grafo = creaGrafo True (1,6)
                     [(i,j,(v!!(i-1))!!(j-1))
                      | i <- [1..6], j <- [1..6]]

v :: [[Int]]
v = [[  0,  4,  1,  6,100,100],
     [  4,  0,  1,100,  5,100],
     [  1,  1,  0,100,  8,  2],
     [  6,100,100,  0,100,  2],
     [100,  5,  8,100,  0,  5],
     [100,100,  2,  2,  5,  0]]

ej2Grafo = creaGrafo True (1,6)
                     [(i,j,(v'!!(i-1))!!(j-1))
                     | i <- [1..6], j <- [1..6]]

v' :: [[Int]]
v' =[[  0,  4,100,100,100,  2],
     [  1,  0,  3,  4,100,100],
     [  6,  3,  0,  7,100,100],
     [  6,100,100,  0,  2,100],
     [100,100,100,  5,  0,100],
     [100,100,100,  2,  3,  0]]

En la matriz del cálculo del camino mínimo, los índices son de la forma (i,j,k) y los valores de la forma (v,xs) representando que el camino mínimo desde el vértice i al j usando los vértices 1, …, k tiene un coste v y está fomado por los vértices xs.

type IndiceCM = (Int,Int,Int)
type ValorCM  = (Int,[Int])

(caminosMinimos g) es la lista de los caminos mínimos entre todos los nodos del grafo g junto con sus costes. Por ejemplo,

λ> caminosMinimos ej1Grafo
[((1,2),(2,[1,3,2])),  ((1,3),(1,[1,3])),  ((1,4),(5,[1,3,6,4])),
 ((1,5),(7,[1,3,2,5])),((1,6),(3,[1,3,6])),((2,3),(1,[2,3])),
 ((2,4),(5,[2,3,6,4])),((2,5),(5,[2,5])),  ((2,6),(3,[2,3,6])),
 ((3,4),(4,[3,6,4])),  ((3,5),(6,[3,2,5])),((3,6),(2,[3,6])),
 ((4,5),(7,[4,6,5])),  ((4,6),(2,[4,6])),  ((5,6),(5,[5,6]))]

Su definición es

caminosMinimos :: (Grafo Int Int) -> [((Int,Int), ValorCM)]
caminosMinimos g =
  [((i,j), valor t (i,j,n)) | i <- [1..n], j <- [i+1..n]]
  where n = length (nodos g)
        t = dinamica (calculaCM g) (cotasCM n)

(calculaCM g t (i,j,k)) es el valor del camino mínimo desde el vértice i al j usando los vértices 1, …, k del grafo g y la tabla t de los valores anteriores al índice (i,j,k).

calculaCM :: (Grafo Int Int) -> Tabla IndiceCM ValorCM -> IndiceCM -> ValorCM
calculaCM g t (i,j,k)
  | k==0      = (peso i j g, if i==j then [i] else [i,j])
  | v1<=v2    = (v1,p)
  | otherwise = (v2,p1++p2)
  where (v1,p)   = valor t (i,j,k-1)
        (a,p1)   = valor t (i,k,k-1)
        (b,_:p2) = valor t (k,j,k-1)
        v2 = a+b

(cotasCM n) son las cotas de la matriz para resolver el problema de los caminos mínimos en un grafo con n nodos.

cotasCM :: Int -> ((Int,Int,Int),(Int,Int,Int))
cotasCM n = ((1,1,0),(n,n,n))

Importación de librerías auxiliares

import Dinamica

-- Nota: Elegir una implementación de los grafos.
import GrafoConVectorDeAdyacencia
-- import GrafoConMatrizDeAdyacencia

Los conjuntos se representan por números enteros.

type Conj = Int

(conj2Lista c) es la lista de los elementos del conjunto c. Por ejemplo,

conj2Lista 24  ==  [3,4]
conj2Lista 30  ==  [1,2,3,4]
conj2Lista 22  ==  [1,2,4]

Su definición es

conj2Lista :: Conj -> [Int]
conj2Lista s = c2l s 0
  where
    c2l 0 _             = []
    c2l n i | odd n     = i : c2l (n `div` 2) (i+1)
            | otherwise = c2l (n `div` 2) (i+1)

maxConj es el máximo número que puede pertenecer al conjunto. Depende de la implementación de Haskell.

maxConj :: Int
maxConj =
  truncate (logBase 2 (fromIntegral maxInt)) - 1
  where maxInt = maxBound::Int

vacio es el conjunto vacío.

vacio :: Conj
vacio = 0

(esVacio c) se verifica si c es el conjunto vacío.

esVacio :: Conj -> Bool
esVacio n = n==0

(conjCompleto n) es el conjunto de los números desde 1 hasta n.

conjCompleto :: Int -> Conj
conjCompleto n
  | (n>=0) && (n<=maxConj) = 2^(n+1)-2
  | otherwise = error ("conjCompleto:" ++ show n)

(inserta x c) es el conjunto obtenido añadiendo el elemento x al conjunto c.

inserta :: Int -> Conj -> Conj
inserta i s
  | i>=0 && i<=maxConj = d'*e+m
  | otherwise          = error ("inserta:" ++ show i)
  where (d,m) = divMod s e
        e     = 2^i
        d'    = if odd d then d else d+1

(elimina x c) es el conjunto obtenido eliminando el elemento x del conjunto c.

elimina :: Int -> Conj -> Conj
elimina i s = d'*e+m
  where (d,m) = divMod s e
        e = 2^i
        d' = if odd d then d-1 else d

Ejemplo de grafo para el problema:

   4       5
+----- 2 -----+
|      |1     |
|  1   |   8  |
1----- 3 -----5
|        \2  /
|  6     2\ /5
+----- 4 --6

La definición del grafo anterior es

ej1 :: Grafo Int Int
ej1 = creaGrafo True (1,6)
                     [(i,j,(v1!!(i-1))!!(j-1))
                      | i <- [1..6], j <- [1..6]]
v1 :: [[Int]]
v1 = [[  0,  4,  1,  6,100,100],
      [  4,  0,  1,100,  5,100],
      [  1,  1,  0,100,  8,  2],
      [  6,100,100,  0,100,  2],
      [100,  5,  8,100,  0,  5],
      [100,100,  2,  2,  5,  0]]

Los índices de la matriz de cálculo son de la forma (i,S) y sus valores (v,xs) donde xs es el camino mínimo desde i hasta n visitando cada vértice de S exactamente una vez y v es el coste de xs.

type IndicePV = (Int,Conj)
type ValorPV  = (Int,[Int])

(viajante g) es el par (v,xs) donde xs es el camino de menor coste que pasa exactamente una vez por todos los nodos del grafo g empezando en su último nodo y v es su coste. Por ejemplo,

λ> viajante ej1
(20,[6,4,1,3,2,5,6])

Su definición es

viajante :: Grafo Int Int -> (Int,[Int])
viajante g = valor t (n,conjCompleto (n-1))
    where n = length (nodos g)
          t = dinamica (calculaPV g n) (cotasPV n)

(calculaPV g n t (i,k)) es el valor del camino mínimo en el grafo g desde i hasta n, calculado usando la tabla t, visitando cada nodo del conjunto k exactamente una vez.

calculaPV :: Grafo Int Int -> Int -> Tabla IndicePV ValorPV -> IndicePV -> ValorPV
calculaPV g n t (i,k)
  | esVacio k = (peso i n g,[i,n])
  | otherwise = minimum [sumaPrim (valor t (j, elimina j k))
                                  (peso i j g)
                         | j <- conj2Lista k]
  where sumaPrim (v,xs) v' = (v+v',i:xs)

(cotasPV n) son las cotas de la matriz de cálculo del problema del viajante en un grafo con n nodos.

cotasPV :: Int -> ((Int,Conj),(Int,Conj))
cotasPV n = ((1,vacio),(n,conjCompleto n))

• Cap. 9: Dynamic programming.