Tema 5: Definiciones de listas por comprensión

Índice

1. Generadores
2. Guardas
- 2.1. Guarda con igualdad
3. La función zip
- 3.1. Las funciones zip, and y listas ordenadas
- 3.2. La función zip y lista de posiciones
4. Comprensión de cadenas
- 4.1. Cadenas y listas
- 4.2. Definiciones sobre cadenas con comprensión
5. Comprensión y dibujos
6. Cifrado César
7. Material complementario
8. Bibliografía

1. Generadores

1.1. Definiciones por comprensión

Definiciones por comprensión en Matemáticas:
\(\{x^2 : x \in \{2,3,4,5\}\} = \{4,9,16,25\}\)
Definiciones por comprensión en Haskell:
```
λ> [x^2 | x <- [2..5]]
[4,9,16,25]
```
La expresión x <- [2..5] se llama un generador.

Ejemplos con más de un generador:

λ> [(x,y) | x <- [1,2,3], y <- [4,5]]
[(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)]
λ> [(x,y) | y <- [4,5], x <- [1,2,3]]
[(1,4),(2,4),(3,4),(1,5),(2,5),(3,5)]

1.2. Generadores dependientes

Ejemplo con generadores dependientes:

λ> [(x,y) | x <- [1..3], y <- [x..3]]
[(1,1),(1,2),(1,3),(2,2),(2,3),(3,3)]

(concat xss) es la concatenación de la lista de listas xss. Por ejemplo,

λ> concat [[1,3],[2,5,6],[4,7]]
[1,3,2,5,6,4,7]

Su definición es

concat :: [[a]] -> [a]
concat xss = [x | xs <- xss, x <- xs]

1.3. Generadores con variables anónimas

Ejemplo de generador con variable anónima: (primeros ps) es la lista de los primeros elementos de la lista de pares ps. Por ejemplo,
```
λ> primeros [(1,3),(2,5),(6,3)]
[1,2,6]
```
Su definición es
```
primeros :: [(a, b)] -> [a]
primeros ps =  [x | (x,_) <- ps]
```

Definición de la longitud por comprensión

length :: [a] -> Int
length xs = sum [1 | _ <- xs]

2. Guardas

Las listas por comprensión pueden tener guardas para restringir los valores.

Ejemplo de guarda:

λ> [x | x <- [1..10], even x]
[2,4,6,8,10]

(factores n) es la lista de los factores del número n. Por ejemplo,

λ> factores 30
[1,2,3,5,6,10,15,30]

Su definición es

factores :: Int -> [Int]
factores n = [x | x <- [1..n], n `mod` x == 0]

(primo n) se verifica si n es primo. Por ejemplo,

primo 30  == False
primo 31  == True

Su definición es

primo :: Int -> Bool
primo n = factores n == [1, n]

(primos n) es la lista de los primos menores o iguales que n. Por ejemplo,

primos 31  == [2,3,5,7,11,13,17,19,23,29,31]

Su definición es

primos :: Int -> [Int]
primos n = [x | x <- [2..n], primo x]

2.1. Guarda con igualdad

Una lista de asociación es una lista de pares formado por una clave y un valor. Por ejemplo,
```
[("Juan",7),("Ana",9),("Eva",3)]
```

(busca c t) es la lista de los valores de la lista de asociación t cuyas claves valen c. Por ejemplo

busca 'b' [('a',1),('b',3),('c',5),('b',2)] ==  [3,2]

Su definición es

busca :: Eq a => a -> [(a, b)] -> [b]
busca c t = [v | (c', v) <- t, c' == c]

3. La función `zip`

La función zip y elementos adyacentes

(zip xs ys) es la lista obtenida emparejando los elementos de las listas xs e ys. Por ejemplo,
```
λ> zip ['a','b','c'] [2,5,4,7]
[('a',2),('b',5),('c',4)]
```

(adyacentes xs) es la lista de los pares de elementos adyacentes de la lista xs. Por ejemplo,

adyacentes [2,5,3,7]  ==  [(2,5),(5,3),(3,7)]

Su definición es

adyacentes :: [a] -> [(a, a)]
adyacentes xs = zip xs (tail xs)

3.1. Las funciones `zip`, `and` y listas ordenadas

(and xs) se verifica si todos los elementos de xs son verdaderos. Por ejemplo,

and [2 < 3, 2+3 == 5]         ==  True
and [2 < 3, 2+3 == 5, 7 < 7]  ==  False

(ordenada xs) se verifica si la lista xs está ordenada. Por ejemplo,

ordenada [1,3,5,6,7]  ==  True
ordenada [1,3,6,5,7]  ==  False

Su definición es

ordenada :: Ord a => [a] -> Bool
ordenada xs = and [x <= y | (x,y) <- adyacentes xs]

3.2. La función `zip` y lista de posiciones

(posiciones x xs) es la lista de las posiciones ocupadas por el elemento x en la lista xs. Por ejemplo,

posiciones 5 [1,5,3,5,5,7]  ==  [1,3,4]

Su definición es

posiciones :: Eq a => a -> [a] -> [Int]
posiciones x xs =
  [i | (x',i) <- zip xs [0..n], x == x']
  where n = length xs - 1

4. Comprensión de cadenas

4.1. Cadenas y listas

Las cadenas son listas de caracteres. Por ejemplo,
```
λ> "abc" == ['a','b','c']
True
```

La expresión

"abc" :: String

es equivalente a

['a','b','c'] :: [Char]

Las funciones sobre listas se aplican a las cadenas:

length "abcde"              ==  5
reverse "abcde"             ==  "edcba"
"abcde" ++ "fg"             ==  "abcdefg"
posiciones 'a' "Salamanca"  ==  [1,3,5,8]

4.2. Definiciones sobre cadenas con comprensión

(minusculas c) es la cadena formada por las letras minúsculas de la cadena c. Por ejemplo,

minusculas "EstoEsUnaPrueba"  ==  "stosnarueba"

Su definición es

minusculas :: String -> String
minusculas xs = [x | x <- xs, elem x ['a'..'z']]

(ocurrencias x xs) es el número de veces que ocurre el carácter x en la cadena xs. Por ejemplo,

ocurrencias 'a' "Salamanca"  ==  4

Su definición es

ocurrencias :: Char -> String -> Int
ocurrencias x xs = length [x' | x' <- xs, x == x']

5. Comprensión y dibujos

En esta sección se amplían los programas de dibujo con CodeWorld/Haskell estudiados en el tema 0.

5.1. Círculos concéntricos

Ejemplo: Escribir un programa para pintar el siguiente dibujo
)

Programa

import CodeWorld

main :: IO ()
main = drawingOf circulosConcentricos

circulosConcentricos :: Picture
circulosConcentricos =
  pictures [circle x | x <- [1,2..9]]

Ejecución en CodeWorld/Haskell: Círculos concéntricos.

5.2. Arcoiris

Ejemplo: Escribir un programa para pintar el siguiente dibujo

Programa:

import CodeWorld

main :: IO()
main = drawingOf arcoiris

arcoiris :: Picture
arcoiris =
  translated 0 (-4) (pictures [ colored c (thickArc 1 0 pi r)
                              | (c,r) <- zip [ white
                                             , purple
                                             , light blue
                                             , blue
                                             , green
                                             , yellow
                                             , orange
                                             , red]
                                             [2..9]])

Ejecución en CodeWorld/Haskell: Arcoiris

5.3. Círculos trasladados

Ejemplo: Escribir un programa para pintar el siguiente dibujo

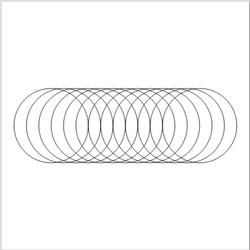
Programa:

import CodeWorld

main :: IO ()
main = drawingOf circulosTrasladados

circulosTrasladados :: Picture
circulosTrasladados =
  pictures [translated x 0 (circle 3) | x <- [-6..6]]

Ejecución en CodeWorld/Haskell: Círculos trasladados

5.4. Círculos trasladados y ampliados

Ejemplo: Escribir un programa para pintar el siguiente dibujo

Programa:

import CodeWorld

main :: IO ()
main = drawingOf circulosTrasladadosAmpliados

circulosTrasladadosAmpliados :: Picture
circulosTrasladadosAmpliados =
  translated (-8) 0 (pictures [translated x 0 (circle x) | x <- [1..8]])

Ejecución en CodeWorld/Haskell: Círculos trasladados y ampliados

5.5. Cuadrados girados

Ejemplo: Escribir un programa para pintar el siguiente dibujo

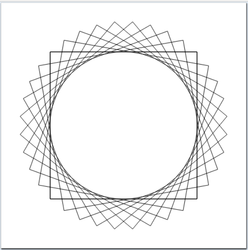
Programa:

import CodeWorld

main :: IO ()
main = drawingOf cuadradosGirados

cuadradosGirados :: Picture
cuadradosGirados =
  pictures [rotated x (rectangle 12 12) | x <- [0,pi/18..pi/2]]

Ejecución en CodeWorld/Haskell: Cuadrados girados

5.6. Círculos en cuadrado

Ejemplo: Escribir un programa para pintar el siguiente dibujo

Programa:

import CodeWorld

main :: IO ()
main = drawingOf circulosEnCuadrado

circulosEnCuadrado :: Picture
circulosEnCuadrado =
  pictures [translated x y (circle 1)
           | x <- [-6,-3..6]
           , y <- [-6,-3..6]]

Ejecución en CodeWorld/Haskell: Círculos en cuadrado

5.7. Círculos en estrella

Ejemplo: Escribir un programa para pintar el siguiente dibujo

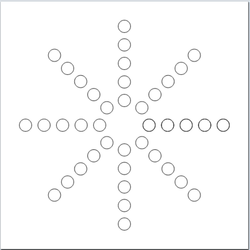
Programa:

import CodeWorld

main :: IO ()
main = drawingOf circulosEnEstrella

circulosEnEstrella :: Picture
circulosEnEstrella =
  pictures [rotated angulo (translated x 0 (circle 0.5))
           | x      <- [2,3.5..8]
           , angulo <- [0, pi/4..2*pi]]

Ejecución en CodeWorld/Haskell: Círculos en estrella

5.8. Círculos expandiéndose

Ejemplo: Escribir un programa para pintar el siguiente dibujo

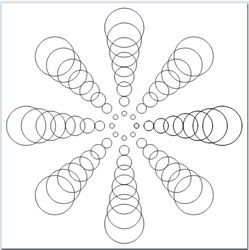
Programa:

import CodeWorld

main :: IO ()
main = drawingOf circulosEnEstrella

circulosEnEstrella :: Picture
circulosEnEstrella =
  pictures [rotated angulo (translated x 0 (circle (x/5)))
           | x      <- [1..8]
           , angulo <- [0, pi/4..2*pi]]

Ejecución en CodeWorld/Haskell: Círculos expandiéndose

5.9. Gráficas de funciones

Ejemplo: Escribir un programa para pintar la parábola (\(y = x^2-8\)):

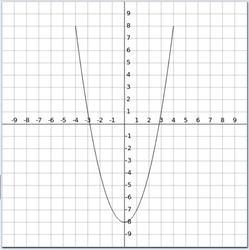
Programa:

import CodeWorld

main :: IO ()
main = drawingOf (graficaSeno <> coordinatePlane)

graficaSeno :: Picture
graficaSeno = curve [(x, x**2-8) | x <- [-4,-3.9..4]]

Ejecución en CodeWorld/Haskell: Gráficas de funciones

6. Cifrado César

En el cifrado César cada letra en el texto original es reemplazada por otra letra que se encuentra 3 posiciones más adelante en el alfabeto.

La codificación de

"en todo la medida"

"hq wrgr od phglgd"

Se puede generalizar desplazando cada letra n posiciones.
La codificación con un desplazamiento 5 de
```
"en todo la medida"
```
es
```
"js ytit qf rjinif"
```
La descodificación de un texto codificado con un desplazamiento n se obtiene codificándolo con un desplazamiento -n.

6.1. Codificación y descodificación

6.1.1. Las funciones `ord` y `char`

(ord c) es el código del carácter c. Por ejemplo,

ord 'a'  ==  97
ord 'b'  ==  98
ord 'A'  ==  65

(char n) es el carácter de código n. Por ejemplo,

chr 97  ==  'a'
chr 98  ==  'b'
chr 65  ==  'A'

Para usar las funciones ord o char hay que importar la librería Data.Char escribiendo al principio del fichero
```
import Data.Char
```

6.1.2. Codificación y descodificación: Código de letra

Simplificación: Sólo se codificarán las letras minúsculas dejando los restantes caracteres sin modificar.

(let2int c) es el entero correspondiente a la letra minúscula c. Por ejemplo,

let2int 'a'  ==  0
let2int 'd'  ==  3
let2int 'z'  ==  25

Su definición es

let2int :: Char -> Int
let2int c = ord c - ord 'a'

6.2. Codificación y descodificación: Letra de código

(int2let n) es la letra minúscula correspondiente al entero n. Por ejemplo,

int2let 0   ==  'a'
int2let 3   ==  'd'
int2let 25  ==  'z'

Su definición es

int2let :: Int -> Char
int2let n = chr (ord 'a' + n)

6.3. Codificación y descodificación: Desplazamiento

(desplaza n c) es el carácter obtenido desplazando n caracteres el carácter c. Por ejemplo,

desplaza   3  'a'  ==  'd'
desplaza   3  'y'  ==  'b'
desplaza (-3) 'd'  ==  'a'
desplaza (-3) 'b'  ==  'y'

Su definición es

desplaza :: Int -> Char -> Char
desplaza n c
  | elem c ['a'..'z'] = int2let ((let2int c+n) `mod` 26)
  | otherwise         = c

6.3.1. Codificación y descodificación

(codifica n xs) es el resultado de codificar el texto xs con un desplazamiento n. Por ejemplo,

λ> codifica   3  "En todo la medida"
"Eq wrgr od phglgd"
λ> codifica (-3) "Eq wrgr od phglgd"
"En todo la medida"

Su definición es

codifica :: Int -> String -> String
codifica n xs = [desplaza n x | x <- xs]

6.3.2. Propiedades de la codificación con QuickCheck

Propiedad: Al desplazar -n un carácter desplazado n, se obtiene el carácter inicial.

prop_desplaza n xs =
    desplaza (-n) (desplaza n xs) == xs

La comprobación es

λ> quickCheck prop_desplaza
+++ OK, passed 100 tests.

Propiedad: Al codificar con -n una cadena codificada con n, se obtiene la cadena inicial.

prop_codifica n xs =
    codifica (-n) (codifica n xs) == xs

La comprobación es

λ> quickCheck prop_codifica
+++ OK, passed 100 tests.

6.4. Análisis de frecuencias

6.4.1. Tabla de frecuencias

Para descifrar mensajes se parte de la frecuencia de aparición de letras.

tabla es la lista de la frecuencias de las letras en castellano, Por ejemplo, la frecuencia de la 'a' es del 12.53%, la de la 'b' es 1.42%.

tabla :: [Float]
tabla = [12.53, 1.42, 4.68, 5.86, 13.68, 0.69, 1.01,
          0.70, 6.25, 0.44, 0.01,  4.97, 3.15, 6.71,
          8.68, 2.51, 0.88, 6.87,  7.98, 4.63, 3.93,
          0.90, 0.02, 0.22, 0.90,  0.52]

6.4.2. Frecuencias

(porcentaje n m) es el porcentaje de n sobre m. Por ejemplo,

porcentaje 2 5  ==  40.0

Su definición es

porcentaje :: Int -> Int -> Float
porcentaje n m = (fromIntegral n / fromIntegral m) * 100

(frecuencias xs) es la frecuencia de cada una de las minúsculas de la cadena xs. Por ejemplo,

λ> frecuencias "en todo la medida"
[14.3,0,0,21.4,14.3,0,0,0,7.1,0,0,7.1,
 7.1,7.1,14.3,0,0,0,0,7.1,0,0,0,0,0,0]

Su definición es

frecuencias :: String -> [Float]
frecuencias xs =
  [porcentaje (ocurrencias x xs) n | x <- ['a'..'z']]
  where n = length (minusculas xs)

6.5. Descifrado

6.6. Descifrado: Ajuste chi cuadrado

Una medida de la discrepancia entre la distribución observada \(os_i\) y la esperada \(es_i\) es
\(\chi^2 = \displaystyle \sum_{i=0}^{n-1}\frac{(os_i-es_i)^2}{es_i}\)
Los menores valores corresponden a menores discrepancias.

(chiCuad os es) es la medida chi cuadrado de las distribuciones os y es. Por ejemplo,

chiCuad [3,5,6] [3,5,6]  ==  0.0
chiCuad [3,5,6] [5,6,3]  ==  3.9666667

Su definición es

chiCuad :: [Float] -> [Float] -> Float
chiCuad os es =
  sum [((o-e)^2)/e | (o,e) <- zip os es]

6.7. Descifrado: Rotación

(rota n xs) es la lista obtenida rotando n posiciones los elementos de la lista xs. Por ejemplo,
```
rota 2 "manolo"  ==  "noloma"
```
Su definición es
```
rota :: Int -> [a] -> [a]
rota n xs = drop n xs ++ take n xs
```

6.8. Descifrado

(descifra xs) es la cadena obtenida descodificando la cadena xs por el antidesplazamiento que produce una distribución de minúsculas con la menor desviación chi cuadrado respecto de la tabla de distribución de las letras en castellano. Por ejemplo,

λ> codifica 5 "Todo para nada"
"Ttit ufwf sfif"
λ> descifra "Ttit ufwf sfif"
"Todo para nada"

Su definición es

descifra :: String -> String
descifra xs =  codifica (-factor) xs
  where
    factor = head (posiciones (minimum tabChi) tabChi)
    tabChi = [chiCuad (rota n tabla') tabla | n <- [0..25]]
    tabla' = frecuencias xs

7. Material complementario

El código del tema se encuentra en este enlace.

Este tema también se encuentra en los siguientes formatos:

Como transparencias en PDF.
Como libro interactivo en IHaskell sobre Jupyter.
Como vídeos de clase:
- Vídeo de la 1ª parte.
- Vídeo de cifrado César.

8. Bibliografía

R. Bird. Introducción a la programación funcional con Haskell. Prentice Hall, 2000.
- Cap. 4: Listas.
G. Hutton. Programming in Haskell. Cambridge University Press.
- Cap. 5: List comprehensions.
B. O'Sullivan, D. Stewart y J. Goerzen. Real World Haskell. O'Reilly, 2008.
- Cap. 12: Barcode Recognition.
B.C. Ruiz, F. Gutiérrez, P. Guerrero y J.E. Gallardo. Razonando con Haskell. Thompson, 2004.
- Cap. 6: Programación con listas.
S. Thompson. Haskell: The Craft of Functional Programming, Second Edition. Addison-Wesley, 1999.
- Cap. 5: Data types: tuples and lists.

Tema 5: Definiciones de listas por comprensión

Índice

1. Generadores

1.1. Definiciones por comprensión

1.2. Generadores dependientes

1.3. Generadores con variables anónimas

2. Guardas

2.1. Guarda con igualdad

3. La función zip

3.1. Las funciones zip, and y listas ordenadas

3.2. La función zip y lista de posiciones

4. Comprensión de cadenas

4.1. Cadenas y listas

4.2. Definiciones sobre cadenas con comprensión

5. Comprensión y dibujos

5.1. Círculos concéntricos

5.2. Arcoiris

5.3. Círculos trasladados

5.4. Círculos trasladados y ampliados

5.5. Cuadrados girados

5.6. Círculos en cuadrado

5.7. Círculos en estrella

5.8. Círculos expandiéndose

5.9. Gráficas de funciones

6. Cifrado César

6.1. Codificación y descodificación

6.1.1. Las funciones ord y char

6.1.2. Codificación y descodificación: Código de letra

6.2. Codificación y descodificación: Letra de código

6.3. Codificación y descodificación: Desplazamiento

6.3.1. Codificación y descodificación

6.3.2. Propiedades de la codificación con QuickCheck

6.4. Análisis de frecuencias

6.4.1. Tabla de frecuencias

6.4.2. Frecuencias

6.5. Descifrado

6.6. Descifrado: Ajuste chi cuadrado

6.7. Descifrado: Rotación

6.8. Descifrado

7. Material complementario

8. Bibliografía

3. La función `zip`

3.1. Las funciones `zip`, `and` y listas ordenadas

3.2. La función `zip` y lista de posiciones

6.1.1. Las funciones `ord` y `char`