Tema 1: Introducción a Prolog

Índice

1. Objetivos del curso
2. Declarativo vs. imperativo
3. Historia de la programación lógica
4. Deducción Prolog en lógica proposicional
5. Deducción Prolog en lógica relacional
6. Deducción Prolog en lógica funcional
7. Ejercicios
8. Bibliografía

1. Objetivos del curso

Lógica como sistema de especificación y lenguaje de programación.
Principios:
- Programas = Teorías.
- Ejecución = Búsqueda de pruebas.
- Programación = Modelización.
Prolog = Programming in Logic.
Relaciones con otros campos:
- Inteligencia artificial.
- Sistemas basados en el conocimiento.
- Procesamiento del lenguaje natural.
Pensar declarativamente.

2. Declarativo vs. imperativo

Paradigmas:
- Imperativo: Se describe cómo resolver el problema/.
- Declarativo: Se describe qué es el problema.
Programas:
- Imperativo: Una sucesión de instrucciones.
- Declarativo: Un conjunto de sentencias.
Lenguajes:
- Imperativo: Pascal, C, Fortran.
- Declarativo: Prolog, Lisp puro, ML, Haskell, DLV, Smodels.
Ventajas;
- Imperativo: Programas rápidos y especializados.
- Declarativo: Programas generales, cortos y legibles.

3. Historia de la programación lógica

1960: Demostración automática de teoremas.
1965: Resolución y unificación (Robinson).
1969: QA3, obtención de respuesta (Green).
1972: Implementación de Prolog (Colmerauer).
1974: Programación lógica (Kowalski).
1977: Prolog de Edimburgo (Warren).
1981: Proyecto japonés de Quinta Generación.
1986: Programación lógica con restricciones.
1995: Estándar ISO de Prolog.

4. Deducción Prolog en lógica proposicional

Base de conocimiento y objetivo:
- Base de conocimiento:
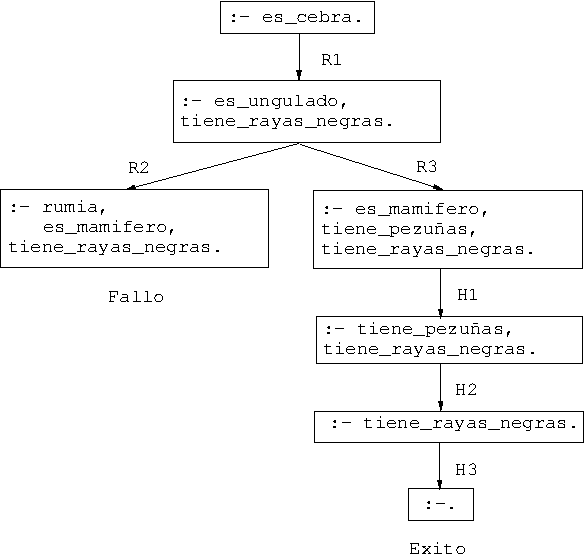
  - Regla 1: Si un animal es ungulado y tiene rayas negras, entonces es una cebra.
  - Regla 2: Si un animal rumia y es mamífero, entonces es ungulado.
  - Regla 3: Si un animal es mamífero y tiene pezuñas, entonces es ungulado.
  - Hecho 1: El animal es mamífero.
  - Hecho 2: El animal tiene pezuñas.
  - Hecho 3: El animal tiene rayas negras.
- Objetivo: Demostrar a partir de la base de conocimientos que el animal es una cebra.

Programa animales.pl

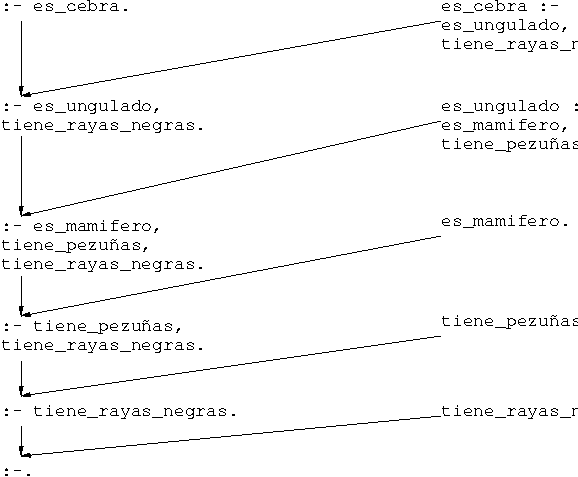
:- dynamic rumia/0.

es_cebra :-
   es_ungulado,
   tiene_rayas_negras.

es_ungulado :-
   rumia,
   es_mamifero.

es_ungulado :-
   es_mamifero,
   tiene_pezuñas.

es_mamifero.
tiene_pezuñas.
tiene_rayas_negras.

Sesión:

> swipl
Welcome to SWI-Prolog (threaded, 64 bits, version 8.2.4)
SWI-Prolog comes with ABSOLUTELY NO WARRANTY. This is free software.
Please run ?- license. for legal details.

For online help and background, visit https://www.swi-prolog.org
For built-in help, use ?- help(Topic). or ?- apropos(Word).

?- [animales].
true.

?- es_cebra.
true.

Árbol de deducción:
Demostración por resolución SLD:

5. Deducción Prolog en lógica relacional

Base de conocimiento:
- Hechos 1-4: 6 y 12 son divisibles por 2 y por 3.
- Hecho 5: 4 es divisible por 2.
- Regla 1: Los números divisibles por 2 y por 3 son divisibles por 6.

Programa divisibilidad.pl

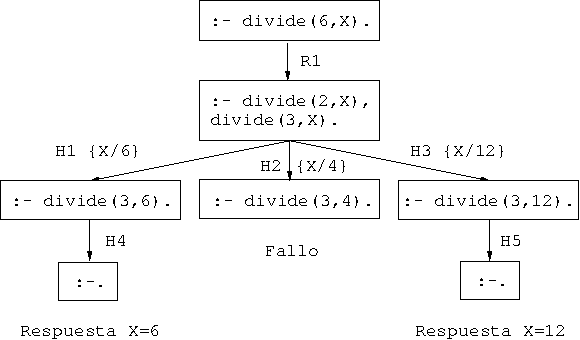
divide(2,6).                             % Hecho 1
divide(2,4).                             % Hecho 2
divide(2,12).                            % Hecho 3
divide(3,6).                             % Hecho 4
divide(3,12).                            % Hecho 5
divide(6,X) :- divide(2,X), divide(3,X). % Regla 1

Símbolos:
- Constantes: 2, 3, 4, 6, 12
- Relación binaria: divide
- Variable: X
Interpretaciones de la Regla 1:
- divide(6,X) :- divide(2,X), divide(3,X).
- Interpretación declarativa:
  \((\forall X)[divide(2,X) \land divide(3,X) \to divide(6,X)]\)
- Interpretación procedimental.
Consulta: ¿Cuáles son los múltiplos de 6?
```
?- divide(6,X).
X = 6 ;
X = 12.
```
Árbol de deducción:
Comentarios:
- Unificación.
- Cálculo de respuestas.
- Respuestas múltiples.

6. Deducción Prolog en lógica funcional

Representación de los números naturales:
- 0, s(0), s(s(0)), …
Definición de la suma:
```
0 + Y = Y
s(X) + Y = s(X+Y)
```

Programa suma.pl

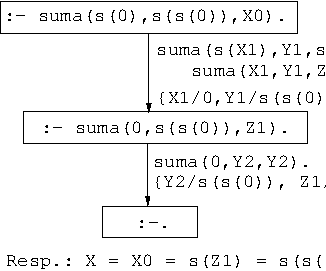
suma(0,Y,Y).                        % R1
suma(s(X),Y,s(Z)) :- suma(X,Y,Z).   % R2

Consulta: ¿Cuál es la suma de s(0) y s(s(0))?

?- suma(s(0),s(s(0)),X).
X = s(s(s(0)))
Yes

Árbol de deducción:
Consulta:
- ¿Cuál es la resta de s(s(s(0))) y s(s(0))?
- Sesión:
```
?- suma(X,s(s(0)),s(s(s(0)))).
X = s(0) ;
No
```
Árbol de deducción:

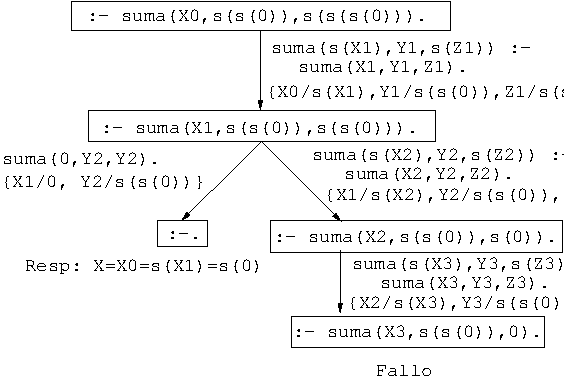
Consulta:

Pregunta: ¿Cuáles son las soluciones de la ecuación
X + Y = s(s(0))?

Sesión:

?- suma(X,Y,s(s(0))).
X = 0         Y = s(s(0)) ;
X = s(0)      Y = s(0) ;
X = s(s(0))   Y = 0 ;
No

Árbol de deducción:
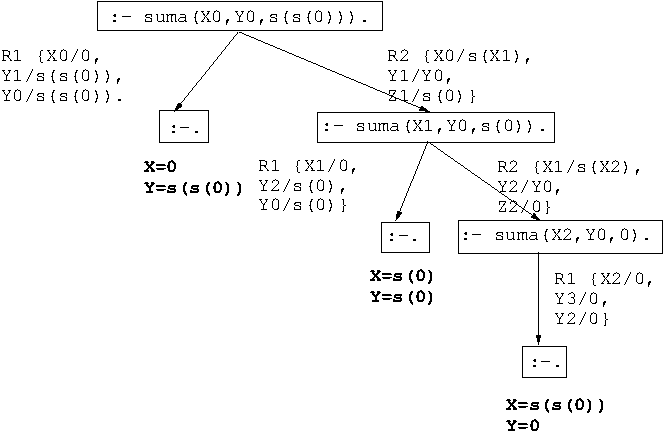
Consulta:
- Pregunta: resolver el sistema de ecuaciones
  1+X=Y
  X+Y=1
- Sesión:
```
?- suma(s(0),X,Y), suma(X,Y,s(0)).
X = 0
Y = s(0) ;
No
```
Árbol de deducción:

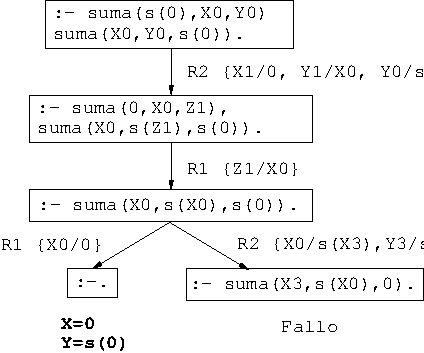
7. Ejercicios

7.1. Deducción en lógica proposicional

Ejercicio 1 Escribir el árbol de deducción y una resolución SLD correspondiente al programa

p :- q, r.   % C1
p :- s.      % C2
q :- s.      % C3
r.           % C4
s.           % C5

y al objetivo

?- p.

Solución

El árbol de deducción es

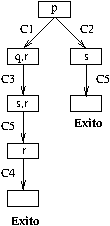
Hay dos resoluciones correspondientes a las dos ramas del árbol. La de la derecha es

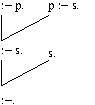
7.2. Deducción en lógica relacional

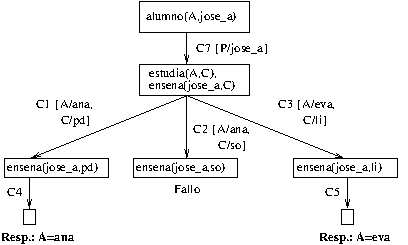
Ejercicio 2 Se considera la siguiente base de conocimiento

estudia(ana,pd).                            % C1
estudia(ana,so).                            % C2
estudia(eva,li).                            % C3
enseña(josé_a,pd).                          % C4
enseña(josé_a,li).                          % C5
enseña(manuel,so).                          % C6
alumno(A,P) :- estudia(A,C), enseña(P,C).   % C7

Escribir el árbol de resolución correspondiente a la base de conocimiento y a la pregunta

?- alumno(A,josé_a).

Solución

El árbol de deducción es

7.3. Deducción en lógica funcional

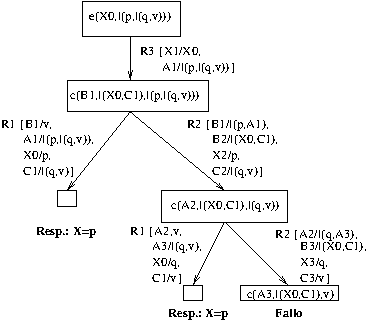
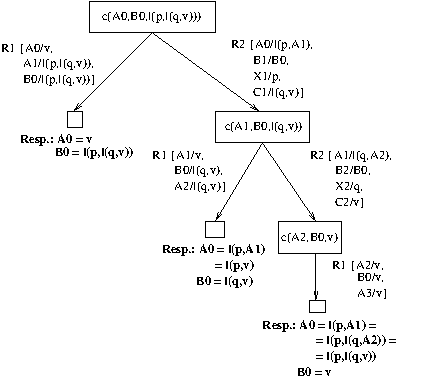
Ejercicio 3. Se considera la siguiente base de conocimiento

c(v,A,A).                         % R1
c(l(X,A),B,l(X,C)) :- c(A,B,C).   % R2
e(X,A) :- c(B,l(X,C),A).          % R3

Escribir los árboles de resolución correspondientes a la base de conocimiento y a las preguntas

?- e(X,l(p,l(q,v))).
?- c(A,B,l(p,l(q,v))).

Nota: Se puede interpretar la base de conocimiento considerando que l(X,A) es la lista de primer elemento X y resto A, v es la lista vacía, c(A,B,C) se verifica si C es la lista obtenida concatenando las listas A y B y e(X,A) se verifica si X pertenece a la lista A.

Solución

El árbol de deducción del apartado 1 es

El árbol de deducción del apartado 2 es

7.4. Base de conocimiento a partir del árbol de deducción

Ejercicio 4. Escribir una base de conocimiento y una pregunta tales que su árbol de resolución tenga la forma siguiente

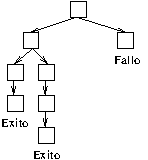
Solución

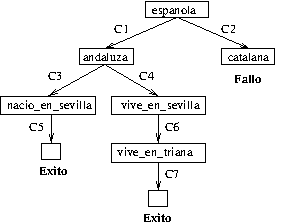
La base de conocimiento

española :- andaluza.                % C1
española :- catalana.                % C2
andaluza :- mujer, nació_en_sevilla. % C3
andaluza :- mujer, vive_en_sevilla.  % C4
mujer.                               % C5
nació_en_sevilla.                    % C6
vive_en_sevilla :- vive_en_triana.   % C7
vive_en_triana.                      % C8

con la pregunta

?- española.

tiene el siguiente árbol de deducción

8. Bibliografía

J.A. Alonso Introducción a la programación lógica con Prolog.
- Cap. 0: Introducción.
I. Bratko Prolog programming for artificial intelligence (3 ed.) (Addison-Wesley, 1990)
- Cap. 1: An overview of Prolog.
- Cap. 2: Syntax and meaning of Prolog programs.
W.F. Clocksin y C.S. Mellish Programming in Prolog. (Springer Verlag, 1994)
- Cap. 1: Tutorial introduction.
- Cap. 2: A closer look.
T. Cornell. Introduction to Prolog. (Universität Tübingen, 1998).
- Cap. 3: Elements of Prolog.
U. Endriss. An introduction to Prolog programming.
- Cap. 1: The basics.
W. Ertel. Introduction to artificial intelligence (2E). (Springer Verlag, 2017).
- Cap. 5: Logic programming with PROLOG.
T. Smith. Artificial intelligence programming in Prolog. (Univ. of Edinburgh, 2004).
- Cap. 3: Prolog basics.
- Cap. 4: How Prolog works.
- Cap. 5: Rules.
J.M. Spivey Introduction to logic programming through Prolog. (Prentice-Hall International, 1996).
- Cap. 1: Introducing logic programming.
- Cap. 2: Programming with relations.