Tema 10: Formalización en Prolog de la lógica proposicional

Índice

1. Sintaxis de la lógica proposicional
2. Semántica de la lógica proposicional
3. Tableros semánticos
4. Bibliografía

Nota: El código correspondiente a este capítulo se encuentra en logica_proposicional.pl.

1. Sintaxis de la lógica proposicional

Alfabeto proposicional:
- símbolos proposicionales.
- conectivas lógicas:
  
  ¬ negación
  
  ∧ conjunción
  
  ∨ disyunción
  
  → condicional
  
  ↔ equivalencia
- símbolos auxiliares: "("` y ")".
Fórmulas proposicionales:
- Los símbolos proposicionales son fórmulas
- Si F y G son fórmulas, entonces también lo son ¬ F, (F ∧ G), (F ∨ G), (F → G) y (F ↔ G).
Eliminación de paréntesis:
- Eliminación de paréntesis externos.
- Precedencia: ¬, ∧, ∨ →, ↔
- Asociatividad: ∧ y ∨ asocian por la derecha
Sintaxis en Prolog

Usual ¬ ∧ ∨ → ↔

Prolog - & v => <=>

Declaración de operadores:

:- op(610, fy,  -).     % negación             
:- op(620, xfy, &).     % conjunción           
:- op(630, xfy, v).     % disyunción           
:- op(640, xfy, =>).    % condicional
:- op(650, xfy, <=>).   % equivalencia

2. Semántica de la lógica proposicional

2.1. Valores y funciones de verdad

2.1.1. Valores de verdad

Valores de verdad:
- 1: verdadero y
- 0: falso
valor_de_verdad(?V) se verifica si V es un valor de verdad.
```
valor_de_verdad(0).
valor_de_verdad(1).
```

2.1.2. Funciones de verdad (negación)

Función de verdad de la negación:

i ¬i

1 0

0 1

i	¬i
1	0
0	1

función_de_verdad(+Op,+V1,-V) si Op(V1) = V.

función_de_verdad(-,  1, 0). 
función_de_verdad(-,  0, 1).

2.1.3. Funciones de verdad de las conectivas binarias

Las funciones de verdad de las conectivas binarias son

i j i ∧ j i ∨ j i → j i ↔ j

1 1 1 1 1 1

1 0 0 1 0 0

0 1 0 1 1 0

0 0 0 0 1 1

i	j	i ∧ j	i ∨ j	i → j	i ↔ j
1	1	1	1	1	1
1	0	0	1	0	0
0	1	0	1	1	0
0	0	0	0	1	1

función_de_verdad(+Op,+V1,+V2,-V) si Op(V1,V2)=V.

función_de_verdad(v,   0, 0, 0) :- !.
función_de_verdad(v,   _, _, 1).
función_de_verdad(&,   1, 1, 1) :- !.
función_de_verdad(&,   _, _, 0).
función_de_verdad(=>,  1, 0, 0) :- !.
función_de_verdad(=>,  _, _, 1).
función_de_verdad(<=>, X, X, 1) :- !.
función_de_verdad(<=>, _, _, 0).

2.2. Valor de una fórmula en una interpretación

2.2.1. Representación de las interpretaciones

Las interpretaciones son listas de pares de variables y valores de verdad. Por ejemplo, [(p,1),(r,0),(u,1)] es una interpretación.

2.2.2. Valor de una fórmula en una interpretación

valor(+F, +I, -V) se verifica si el valor de la fórmula F en la interpretación I es V. Por ejemplo,

?- valor((p v q) & (-q v r),[(p,1),(q,0),(r,1)],V).
V = 1 
?- valor((p v q) & (-q v r),[(p,0),(q,0),(r,1)],V).
V = 0

Su definición es

valor(F, I, V) :-
   memberchk((F,V), I).
valor(-A, I, V) :-
   valor(A, I, VA),
   función_de_verdad(-, VA, V).
valor(F, I, V) :-
   F =..[Op, A, B],
   valor(A, I, VA),
   valor(B, I, VB),
   función_de_verdad(Op, VA, VB, V).

2.3. Interpretaciones principales de una fórmula

2.3.1. Interpretaciones de una fórmula

I es una interpretación principal de F si es una aplicación del conjunto de los símbolos proposicionales de F en el conjunto de los valores de verdad.

interpretaciones_fórmula(+F,-L) se verifica si L es el conjunto de las interpretaciones principales de la fórmula F. Por ejemplo,

?- interpretaciones_fórmula((p v q) & (-q v r),L).
L = [[ (p, 0),  (q, 0),  (r, 0)],
     [ (p, 0),  (q, 0),  (r, 1)],
     [ (p, 0),  (q, 1),  (r, 0)],
     [ (p, 0),  (q, 1),  (r, 1)],
     [ (p, 1),  (q, 0),  (r, 0)],
     [ (p, 1),  (q, 0),  (r, 1)],
     [ (p, 1),  (q, 1),  (r, 0)],
     [ (p, 1),  (q, 1),  (r, 1)]]

Su definición es

interpretaciones_fórmula(F,U) :-
   findall(I,interpretación_fórmula(I,F),U).

interpretación_fórmula(?I,+F) se verifica si I es una interpretación de la fórmula F. Por ejemplo,

?- interpretación_fórmula(I,(p v q) & (-q v r)).
I = [ (p, 0),  (q, 0),  (r, 0)] ;
I = [ (p, 0),  (q, 0),  (r, 1)] ;
I = [ (p, 0),  (q, 1),  (r, 0)] ;
I = [ (p, 0),  (q, 1),  (r, 1)] ;
I = [ (p, 1),  (q, 0),  (r, 0)] 
true.

Su definición es

interpretación_fórmula(I,F) :-
   símbolos_fórmula(F,U),
   interpretación_símbolos(U,I).

2.3.2. Símbolos de una fórmula

símbolos_fórmula(+F,?U) se verifica si U es el conjunto ordenado de los símbolos proposicionales de la fórmula F. Por ejemplo,

?- símbolos_fórmula((p v q) & (-q v r), U).
U = [p, q, r]

Su definición es

símbolos_fórmula(F,U) :-
   símbolos_fórmula_aux(F,U1),
   sort(U1,U).

símbolos_fórmula_aux(F,[F]) :-
   atom(F).
símbolos_fórmula_aux(-F,U) :-
   símbolos_fórmula_aux(F,U).
símbolos_fórmula_aux(F,U) :-
   F =.. [_Op,A,B],
   símbolos_fórmula_aux(A,UA),
   símbolos_fórmula_aux(B,UB),
   union(UA,UB,U).

2.3.3. Interpretación de una lista de símbolos

interpretación_símbolos(+L,-I) se verifica si I es una interpretación de la lista de símbolos proposicionales L. Por ejemplo,

?- interpretación_símbolos([p,q],I).
I = [ (p, 0),  (q, 0)] ;
I = [ (p, 0),  (q, 1)] ;
I = [ (p, 1),  (q, 0)] ;
I = [ (p, 1),  (q, 1)].

Su definición es

interpretación_símbolos([],[]).
interpretación_símbolos([A|L],[(A,V)|IL]) :-
   valor_de_verdad(V),
   interpretación_símbolos(L,IL).

2.4. Modelo de una fórmula

es_modelo_fórmula(+I,+F) se verifica si la interpretación I es un modelo de la fórmula F (es decir, si el valor de F en I es verdadero). Por ejemplo,

?- es_modelo_fórmula([(p,1),(q,0),(r,1)], (p v q) & (-q v r)).
true.
?- es_modelo_fórmula([(p,0),(q,0),(r,1)], (p v q) & (-q v r)).
false.

Su definición es

es_modelo_fórmula(I,F) :-
   valor(F,I,V),
   V = 1.

2.5. Cálculo de los modelos de una fórmula

modelo_fórmula(?I,+F) se verifica si I es un modelo principal de la fórmula F. Por ejemplo,

?- modelo_fórmula(I,(p v q) & (-q v r)).
I = [ (p, 0),  (q, 1),  (r, 1)] ;
I = [ (p, 1),  (q, 0),  (r, 0)] ;
I = [ (p, 1),  (q, 0),  (r, 1)] ;
I = [ (p, 1),  (q, 1),  (r, 1)] ;
false.

Su definición es

modelo_fórmula(I,F) :-
   interpretación_fórmula(I,F),
   es_modelo_fórmula(I,F).

modelos_fórmula(+F,-L) se verifica si L es el conjunto de los modelos principales de la fórmula F. Por ejemplo,

?- modelos_fórmula((p v q) & (-q v r),L).
L = [[ (p, 0),  (q, 1),  (r, 1)],
     [ (p, 1),  (q, 0),  (r, 0)],
     [ (p, 1),  (q, 0),  (r, 1)],
     [ (p, 1),  (q, 1),  (r, 1)]]

Su definición es

modelos_fórmula(F,L) :-
   findall(I,modelo_fórmula(I,F),L).

2.6. Satisfacibilidad

es_satisfacible(+F) se verifica si la fórmula F es satisfacible (es decir, si tiene modelos). Por ejemplo,

?- es_satisfacible((p v q) & (-q v r)).
true.
?- es_satisfacible((p & q) & (p => r) & (q => -r)).
false.

Su definición es

es_satisfacible(F) :-
   interpretación_fórmula(I,F),
   es_modelo_fórmula(I,F).

2.7. Contramodelo de una fórmula

contramodelo_fórmula(?I,+F) se verifica si I es un contramodelo principal de la fórmula F (es decir, si I es una interpretación principal de F que no es modelo de F). Por ejemplo,

?- contramodelo_fórmula(I, p <=> q).
I = [ (p, 0),  (q, 1)] ;
I = [ (p, 1),  (q, 0)] ;
false.
?- contramodelo_fórmula(I, p => p).
false.

Su definición es

contramodelo_fórmula(I,F) :-
   interpretación_fórmula(I,F),
   not(es_modelo_fórmula(I,F)).

2.8. Fórmulas válidas (tautologías)

es_tautología(+F) se verifica si la fórmula F es una tautología (es decir, si todas las interpretaciones son modelos de F). Por ejemplo,
```
?- es_tautología((p => q) v (q => p)).
true.
?- es_tautología(p => q).
false.
```
Su definición es
```
es_tautología(F) :-
   not(contramodelo_fórmula(_I,F)).
```

Una definición alternativa es

es_tautología_alt(F) :-
   not(es_satisfacible(-F)).

2.9. Interpretaciones principales de un conjunto de fórmulas

Una interpretación principal de un conjunto de fórmulas es una aplicación del conjunto de sus símbolos proposicionales en el conjunto de los valores de verdad.

interpretaciones_conjunto(+S,-L) se verifica si L es el conjunto de las interpretaciones principales del conjunto S. Por ejemplo,

?- interpretaciones_conjunto([p => q, q=> r],U).
U = [[(p,0), (q,0), (r,0)], [(p,0), (q,0), (r,1)],
     [(p,0), (q,1), (r,0)], [(p,0), (q,1), (r,1)],
     [(p,1), (q,0), (r,0)], [(p,1), (q,0), (r,1)],
     [(p,1), (q,1), (r,0)], [(p,1), (q,1), (r,1)]]

Su definición es

interpretaciones_conjunto(S,U) :-
   findall(I,interpretación_conjunto(I,S),U).

interpretación_conjunto(?I,+S) se verifica si I es una interpretación del conjunto de fórmulas S. Por ejemplo,

?- interpretación_conjunto(I,[p => q, q => p & q]).
I = [ (p, 0),  (q, 0)] ;
I = [ (p, 0),  (q, 1)] ;
I = [ (p, 1),  (q, 0)] ;
I = [ (p, 1),  (q, 1)] ;
false.

Su definición es

interpretación_conjunto(I,S) :-
   símbolos_conjunto(S,U),
   interpretación_símbolos(U,I).

símbolos_conjunto(+S,?U) se verifica si U es el conjunto ordenado de los símbolos proposicionales del conjunto de fórmulas S. Por ejemplo,

?- símbolos_conjunto([p => q, q=> r],U).
U = [p, q, r]

Su definición es

símbolos_conjunto(S,U) :-
   símbolos_conjunto_aux(S,U1),
   sort(U1,U).

símbolos_conjunto_aux([],[]).
símbolos_conjunto_aux([F|S],U) :-
   símbolos_fórmula(F,U1),
   símbolos_conjunto_aux(S,U2),
   union(U1,U2,U).

2.10. Modelo de un conjunto de fórmulas

es_modelo_conjunto(+I,+S) se verifica si la interpretación I es un modelo del conjunto de fórmulas S (es decir, si I es modelo de todas las fórmulas de S). Por ejemplo,

?- es_modelo_conjunto([(p,1),(q,0),(r,1)], [(p v q) & (-q v r),q => r]).
true.
?- es_modelo_conjunto([(p,0),(q,1),(r,0)], [(p v q) & (-q v r),q => r]).
false.

Su definición es

es_modelo_conjunto(_I,[]).
es_modelo_conjunto(I,[F|S]) :-
   es_modelo_fórmula(I,F),
   es_modelo_conjunto(I,S).

2.11. Cálculo de modelos de conjuntos de fórmulas

modelo_conjunto(?I,+S) se verifica si I es un modelo principal del conjunto de fórmulas S. Por ejemplo,

?- modelo_conjunto(I,[(p v q) & (-q v r),p => r]).
I = [ (p, 0),  (q, 1),  (r, 1)] ;
I = [ (p, 1),  (q, 0),  (r, 1)] ;
I = [ (p, 1),  (q, 1),  (r, 1)] ;
false.

Su definición es

modelo_conjunto(I,S) :-
   interpretación_conjunto(I,S),
   es_modelo_conjunto(I,S).

modelos_conjunto(+S,-L) se verifica si L es el conjunto de los modelos principales del conjunto de fórmulas S. Por ejemplo,

?- modelos_conjunto([(p v q) & (-q v r),p => r],L).
L = [[ (p, 0),  (q, 1),  (r, 1)],
     [ (p, 1),  (q, 0),  (r, 1)],
     [ (p, 1),  (q, 1),  (r, 1)]]

Su definición es

modelos_conjunto(S,L) :-
   findall(I,modelo_conjunto(I,S),L).

2.12. Consistencia de un conjunto de fórmulas

consistente(+S) se verifica si el conjunto de fórmulas S es consistente (es decir, tiene modelos). Por ejemplo,

?- consistente([(p v q) & (-q v r),p => r]).
true.
?- consistente([(p v q) & (-q v r),p => r, -r]).
false.

Su definición es

consistente(S) :-
   modelo_conjunto(_I,S), !.

inconsistente(+S) se verifica si el conjunto de fórmulas S es inconsistente (es decir, no tiene modelos).
```
inconsistente(S) :-
   not(modelo_conjunto(_I,S)).
```

2.13. Consecuencia lógica

es_consecuencia(+S,+F) se verifica si la fórmula F es consecuencia del conjunto de fórmulas S (es decir, si todos los modelos de S son modelos de F). Por ejemplo,
```
?- es_consecuencia([p => q, q => r], p => r).
true.
?- es_consecuencia([p], p & q).
false.
```
Su definición es
```
es_consecuencia(S,F) :-
   not(contramodelo_consecuencia(S,F,_I)).
```

contramodelo_consecuencia(+S,+F,?I) se verifica si I es una interpretación principal de $~S~ ∪ \{~F~\}$ que es modelo del conjunto de fórmulas S pero no es modelo de la fórmula F. Por ejemplo,

?- contramodelo_consecuencia([p], p & q, I).
I = [ (p, 1),  (q, 0)] ;
false.
?- contramodelo_consecuencia([p => q, q=> r], p => r, I).
false.

Su definición es

contramodelo_consecuencia(S,F,I) :-
   interpretación_conjunto(I,[F|S]),
   es_modelo_conjunto(I,S),
   not(es_modelo_fórmula(I,F)).

Una definición alternativa de es_consecuencia es

es_consecuencia_alt(S,F) :-
   inconsistente([-F|S]).

2.14. El problema de los veraces y mentirosos

Enunciado: En una isla hay dos tribus, la de los veraces (que siempre dicen la verdad) y la de los mentirosos (que siempre mienten). Un viajero se encuentra con tres isleños A, B y C y cada uno le dice una frase
- A dice "B y C son veraces syss C es veraz"
- B dice "Si A y B son veraces, entonces B y C son veraces y A es mentiroso"
- C dice "B es mentiroso syss A o B es veraz"
Determinar a qué tribu pertenecen A, B y C.
Representación:
- a, b y c representan que A, B y C son veraces \newline
- -a, -b y -c representan que A, B y C son mentirosos

Las tribus se determinan a partir de los modelos del conjunto de fórmulas correspondientes a las tres frases.

?- modelos_conjunto([a <=> (b & c <=> c),
                     b <=> (a & c => b & c & -a),
                     c <=> (-b <=> a v b)],
                    L).
L = [[ (a, 1), (b, 1), (c, 0)]]

Por tanto, A y B son veraces y C es mentiroso.

3. Tableros semánticos

3.1. Demostraciones mediante tableros semánticos

Demostración de fórmula válida:
¬ p ∨ ¬ q → ¬(p ∧ q) es válida
syss {¬(¬ p ∨ ¬ q → ¬(p ∧ q))} es inconsistente
syss {¬ p ∨ ¬ q, ¬¬(p ∧ q)} es inconsistente
syss {¬ p ∨ ¬ q, p ∧ q} es inconsistente
syss {p, q, ¬ p ∨ ¬ q} es inconsistente
syss {p, q, ¬ p} y \{p, q, ¬ q} son inconsistentes
Tablero semántico:
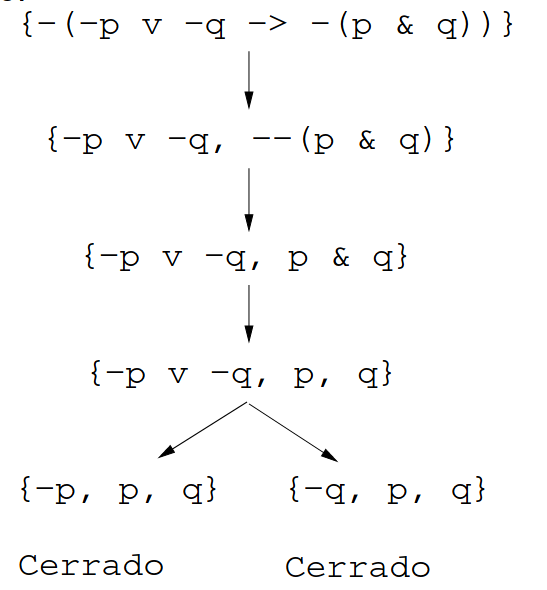
Demostración de fórmula no válida: ¬ p ∨ ¬ q → ¬(p ∧ r) es válida
syss {¬(¬ p ∨ ¬ q → ¬(p ∧ r))} es inconsistente
syss {¬ p ∨ ¬ q, ¬¬(p ∧ r)} es inconsistente
syss {¬ p ∨ ¬ q, p ∧ r} es inconsistente
syss {p, q, ¬ p ∨ ¬ r} es inconsistente
syss {p, q, ¬ p} y \{p, q, ¬ r} son inconsistentes
Tablero semántico:

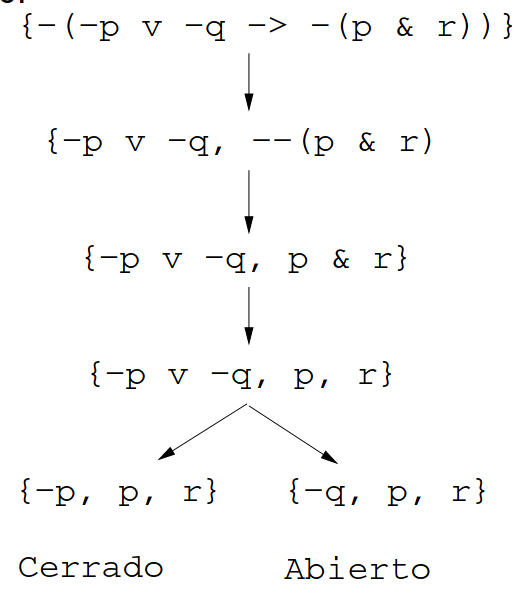
3.2. Notación uniforme

3.2.1. Literales

Los literales son los átomos y sus negaciones.

literal(+F) se verifica si la fórmula F es un literal.

literal(F)  :- 
   atom(F).
literal(-F) :- 
   atom(F).

3.2.2. Dobles negaciones

La fórmula F es una doble negación si existe una fórmula G tal que F es de la forma ¬¬G.
Si F es ¬¬G, entonces ⊨ F ↔ G.

3.2.3. Fórmulas alfa

Las fórmulas alfa, junto con sus componentes, son las siguientes

Fórmula 1ª componente 2ª componente

A₁ ∧ A₂ A₁ A₂

¬(A₁ → A₂) A₁ ¬A₂

¬(A₁ ∨ A₂) ¬A₁ ¬A₂
Si F es una fórmula alfa y sus componentes son F₁ y F₂, entonces ⊨ F ↔ F₁ ∧ F₂.

Fórmula	1ª componente	2ª componente
A₁ ∧ A₂	A₁	A₂
¬(A₁ → A₂)	A₁	¬A₂
¬(A₁ ∨ A₂)	¬A₁	¬A₂

alfa(+A,-A1,-A2) se verifica si A es una fórmula alfa y sus componentes son A1 y A2.

alfa(A1 & A2,     A1,  A2).
alfa(-(A1 => A2), A1,  -A2).
alfa(-(A1 v A2),  -A1, -A2).

3.2.4. Fórmulas beta

Las fórmulas beta, junto con sus componentes, son las siguientes:

Fórmula	1ª componente	2ª componente
B₁ ∨ B₂	B₁	B₂
B₁ → B₂	¬B₁	B₂
¬(B₁ ∧ B₂)	¬B₁	¬B₂
B₁ ↔ B₂	B₁ ∧ B₂	¬B₁ ∧ ¬B₂
¬(B₁ ↔ B₂)	B₁ ∧ ¬ B₂	¬B₁ ∧ B₂

Si F es una fórmula beta y sus componentes son F₁ y F₂, entonces ⊨ F ↔ F₁ ∨ F₂.

beta(+B,-B1,-B2) se verifica si B es una fórmula beta y sus componentes son B1 y B2.

beta(B1 v B2,      B1,       B2).
beta(B1 => B2,     -B1,      B2).
beta(-(B1 & B2),   -B1,      -B2).
beta(B1 <=> B2,    B1 & B2,  -B1 & -B2).
beta(-(B1 <=> B2), B1 & -B2, -B1 & B2).

3.3. Procedimiento de completación de tableros

Un conjunto de fórmulas es cerrado si contiene una fórmula y su negación,
Un conjunto de fórmulas es abierto si es un conjunto de literales que no contiene una fórmula y su negación.
Construcción del tablero de un conjunto de fórmulas $S$.
- (I) El árbol cuyo único nodo tiene como etiqueta S es un tablero de S.
- (C) Sea 𝑻 un tablero de S y S₁ la etiqueta de una hoja de 𝑻.
  - (C.1) Si S₁ es cerrado, entonces el árbol obtenido añadiendo como hijo de S₁ el nodo etiquetado con cerrado es un tablero de S.
  - (C.2) Si S₁ es abierto, entonces el árbol obtenido añadiendo como hijo de S₁ el nodo etiquetado con abierto es un tablero de S.
  - (C.3) Si S₁ contiene una doble negación ¬¬ F, entonces el árbol obtenido añadiendo como hijo de S₁ el nodo etiquetado con (S₁ - {¬¬F\}) ∪ {F} es un tablero de S.
  - (C.4) Si S₁ contiene una fórmula alfa F de componentes F₁ y F₂, entonces el árbol obtenido añadiendo como hijo de S₁ el nodo etiquetado con (S₁ - {F}) ∪ {F₁,F₂} es un tablero de S.
  - (C.5) Si S₁ contiene una fórmula beta F de componentes F₁ y F₂, entonces el árbol obtenido añadiendo como hijos de S₁ los nodos etiquetados con (S₁ - {F}) ∪ {F₁} y (S₁ - {F}) ∪ {F₂} es un tablero de S.
Un tablero semántico de S es completo si no se le puede aplicar ninguna de las reglas de expansión; es decir, todas sus hojas son abiertas o cerradas.
Representación de tableros: t(S,Izq,Dcha) representa el tablero de raíz S, rama izquierda Izq y rama derecha Dcha.

tablero_completo(+S,-Tab) se verifica si Tab es un tablero completo del conjunto S. Por ejemplo,

?- tablero_completo([- (-p v -q => - (p & r))],T).
T = t([- (-p v -q => - (p & r))],
      t([-p v -q, - -(p & r)],
        t([p & r, -p v -q],
          t([p, r, -p v -q],
            t([-p, p, r], cerrado, vacio),
            t([-q, p, r], abierto, vacio)),
          vacio),
        vacio),
      vacio) 
true.

Su definición es

tablero_completo(S,Tab) :- 
   completación(t(S,_Izq,_Dcha),Tab).

completación(+Tab1,-Tab2) se verifica si Tab2 es una completación (i.e. un tablero completo) del tablero Tab1.

completación(t(Flas,Izq1,Dcha1),t(Flas,Izq3,Dcha3)) :-
   paso(t(Flas,Izq1,Dcha1),t(Flas,Izq2,Dcha2)), !,
   completación(Izq2,Izq3),
   completación(Dcha2,Dcha3).
completación(Tab,Tab).

paso(+Tab1,-Tab2) se verifica si Tab2 es un tablero obtenido aplicando una regla de completación al tablero Tab1.

paso(t(S1,_,_),t(S1, cerrado, vacio)) :- % C1
   cerrada(S1), !.
paso(t(S1,_,_),t(S1, abierto, vacio)) :- % C2
   lista_de_literales(S1), !.
paso(t(S1,_,_),t(S1, Izq, vacio)) :-     % C3
   regla_doble_negacion(S1, S2), !,
   Izq = t(S2, _, _).
paso(t(S1,_,_),t(S1, Izq, vacio)) :-     % C4
   regla_alfa(S1, S2), !,
   Izq = t(S2, _, _).
paso(t(S1,_,_),t(S1, Izq, Dcha)) :-      % C5
   regla_beta(S1, S2, S3),
   Izq  = t(S2, _, _),
   Dcha = t(S3, _, _).

cerrada(+S) se verifica si S es una lista cerrada (i.e. que contiene una fórmula y su negación).
```
cerrada(S) :- 
   member(-F,S), 
   member(F,S).
```

lista_de_literales(+S) se verifica si S es una lista de literales.

lista_de_literales([]).
lista_de_literales([F|S]) :-
   literal(F),
   lista_de_literales(S).

regla_doble_negacion(+S1,-S2) se verifica si S1 es una lista de fórmulas que contiene una doble negación --F y S2 es la lista de fórmulas obtenidas sustituyendo en S1 la fórmula --F por F. Por ejemplo,

?- regla_doble_negacion([- -(q v r), p => r],L).
L = [q v r, p => r] 
?- regla_doble_negacion([p v (q v r), p => r],L).  
No

Su definición es

regla_doble_negacion(S1, [F|S2]) :-
   member(- -F, S1), !,
   delete(S1, - -F, S2).

regla_alfa(+S1,-S2) se verifica si S1 es una lista de fórmulas que contiene una fórmula alfa A y S2 es la lista de fórmulas obtenidas sustituyendo en S1 la fórmula A por sus componentes. Por ejemplo,

?- regla_alfa([p & (q v r), p => r],L).
L = [p, q v r, p => r] 
?- regla_alfa([p v (q v r), p => r],L).  
true.

Su definición es

regla_alfa(S1, [A1,A2|S2]) :-
   member(A, S1),
   alfa(A, A1, A2), !,
   delete(S1, A, S2).

regla_beta(+S1,-S2,-S3) se verifica si S1 es una lista de fórmulas que contiene al menos una fórmula beta B y S2 es la lista de fórmulas obtenidas sustituyendo en S1 la fórmula B por una de sus componentes y S3, por la otra. Por ejemplo,

?- regla_beta([p & (q v r), p => r],L1,L2).
L1 = [-p, p & (q v r)]
L2 = [r, p & (q v r)] 
?- regla_beta([p & (q v r), -(p => r)],L1,L2).
false.

Su definición es

regla_beta(S1, [B1|RS1], [B2|RS1]) :-
   member(B, S1),
   beta(B, B1, B2),
   delete(S1, B, RS1).

3.4. Tableros cerrados

es_cerrado(+Tab) se verifica si Tab es un tablero cerrado (es decir, si todas sus hojas están etiquetadas con cerrado o vacio).
```
es_cerrado(t(_,Izq,Dcha)) :-
   es_cerrado(Izq),
   es_cerrado(Dcha).
es_cerrado(cerrado).
es_cerrado(vacio).
```

3.5. Teorema por tableros

3.5.1. Prueba mediante tableros

prueba(+F,-Tab) se verifica si Tab es una prueba de la fórmula F (es decir, un tablero completo cerrado de {¬F}). Por ejemplo,

?- prueba(-p v -q => -(p & q),T).
T = t([- (-p v-q => - (p & q))],
      t([-p v-q, - -(p & q)],
        t([p & q, -p v -q],
          t([p, q, -p v -q],
            t([-p, p, q], cerrado, vacio),
            t([-q, p, q], cerrado, vacio)),
          vacio),
        vacio),
      vacio)
?- prueba(-p v -q => -p,T).
false.

Su definición es

prueba(F,Tab) :-
   tablero_completo([-F],Tab), !,
   es_cerrado(Tab).

3.5.2. Teorema mediante tableros

es_teorema(+F) se verifica si la fórmula F es teorema mediante tableros semánticos (es decir, F tiene una prueba mediante tableros). Por ejemplo,
```
?- es_teorema(-p v -q => -(p & q)).
true.
?- es_teorema(-p v -q => -(p & r)).
false.
```
Su definición es
```
es_teorema(F) :-
   prueba(F,_Tab).
```
El cálculo de tableros semánticos es adecuado y completo; es decir, una fórmula es válida syss es teorema mediante tableros semánticos.

3.6. Deducción por tableros

3.6.1. Deducción por tableros

prueba_deducible_tab(+S,+F,-Tab) se verifica si Tab es una prueba por tableros semánticos de que la fórmula F es deducible del conjunto de fórmulas S (es decir, Tab es un tablero completo cerrado de S ∪ {¬F}$. Por ejemplo,

?- prueba_deducible_tab([p => q, q => r], p => r,T).
T = t([- (p => r), p => q, q => r],
      t([p, -r, p => q, q => r],
        t([-p, p, -r, q => r], cerrado, vacio),
        t([q, p, -r, q => r],
          t([-q, q, p, -r], cerrado, vacio),
          t([r, q, p, -r], cerrado, vacio))),
      vacio) 
true.
?- prueba_deducible_tab([p => q, q => r], p <=> r,T). 
false.

Gráficamente,
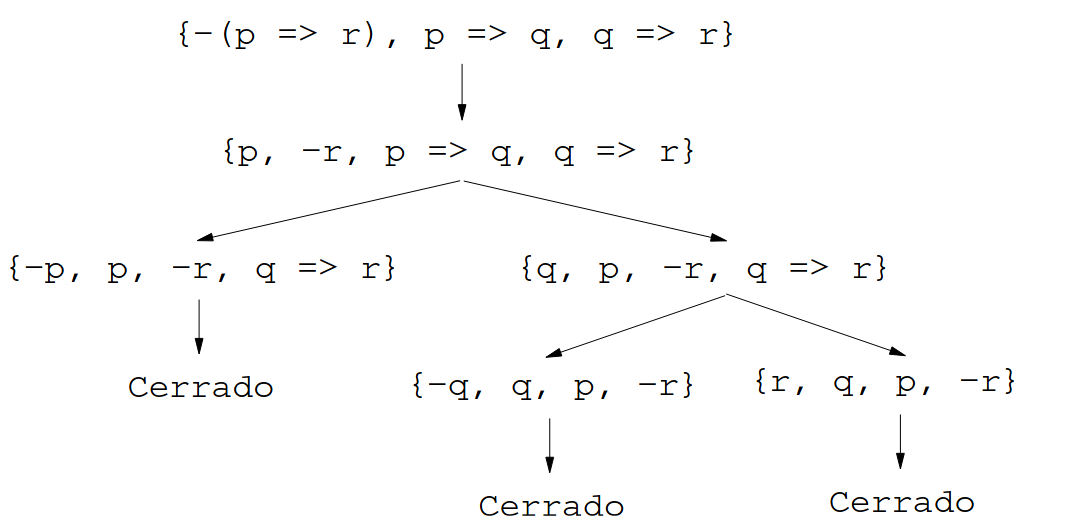Su definición es

prueba_deducible_tab(S,F,Tab) :-
   tablero_completo([-F|S],Tab), !,
   es_cerrado(Tab).

3.6.2. Deducibilidad por tableros

es_deducible_tab(+S,+F) se verifica si la fórmula F es deducible (mediante tableros) del conjunto de fórmulas S.
```
es_deducible_tab(S,F) :-
   prueba_deducible_tab(S,F,_Tab).
```
La fórmula F es consecuencia de S syss F es deducible mediante tableros a partir de S.

4. Bibliografía

J.A. Alonso y J. Borrego. Deducción automática (Vol. 1: Construcción lógica de sistemas lógicos). (Ed. Kronos, 2002).
- Cap. 3: Elementos de lógica proposicional.
- Cap. 4.1: Tableros semánticos.
M. Ben-Ari. Mathematical Logic for Computer Science (2nd ed.) (Springer, 2001).
- Cap. 2: Propositional calculus: Formulas, models, tableaux.
M. Fitting. First-order logic and automated theorem proving (2nd ed.) (Springer, 1995).
A. Nerode y E.A. Shore. Logic for applications. (Springer, 1997)

¬	negación
∧	conjunción
∨	disyunción
→	condicional
↔	equivalencia

Usual	¬	∧	∨	→	↔
Prolog	`-`	`&`	`v`	`=>`	`<=>`