Tema 14: Programación de metaintérpretes

Índice

1. Base de conocimiento del sistema eléctrico
2. Metaintérpretes simples
3. Metaintérprete con preguntas
4. Metaintérprete con explicación
5. Bibliografía

1. Base de conocimiento del sistema eléctrico

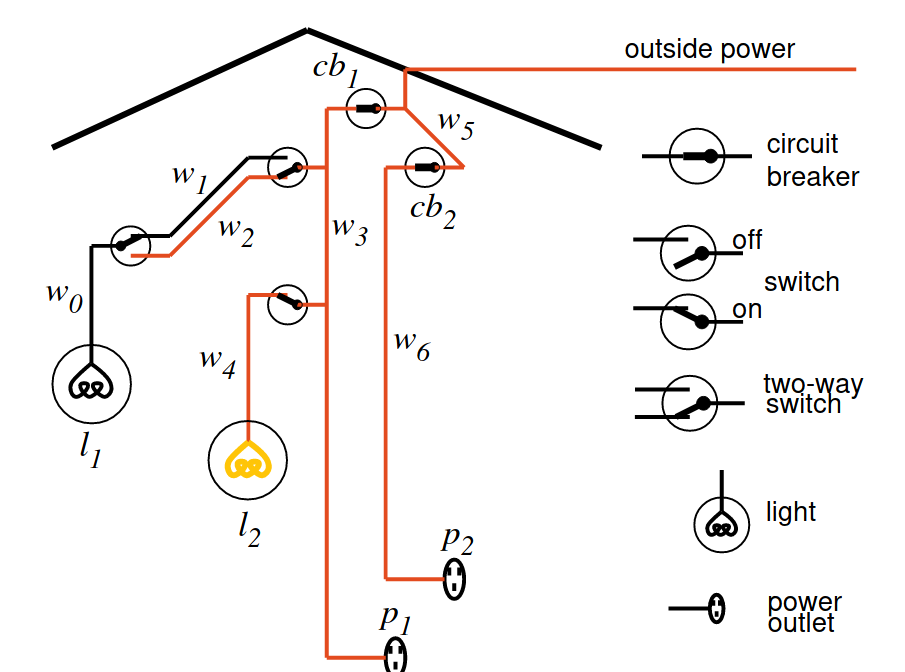
El sistema eléctrico que se va a representar es el siguiente (Poole-98 p. 16)

Operadores

:- op(1100, xfx, <-).
:- op(1000, xfy, &).

luz(?L) se verifica si L es una luz
```
luz(l1) <- verdad.
luz(l2) <- verdad.
```
abajo(?I) se verifica si el interruptor I está hacia abajo.
```
abajo(i1) <- verdad.
```
arriba(?I) se verifica si el interruptor I está hacia arriba.
```
arriba(i2) <- verdad.   arriba(i3) <- verdad.
```

está_bien(?X) se verifica si la luz (o cortacircuito) X está bien.

está_bien(l1) <- verdad.   
está_bien(l2) <- verdad.
está_bien(cc1) <- verdad.  
está_bien(cc2) <- verdad.

conectado(?D1,?D2) se verifica si los dispositivos D1 y D2 están conectados (de forma que puede fluir la corriente eléctrica de D2 a D1).

conectado(l1,c0) <- verdad.
conectado(c0,c1) <- arriba(i2).
conectado(c0,c2) <- abajo(i2).
conectado(c1,c3) <- arriba(i1).
conectado(c2,c3) <- abajo(i1).
conectado(l2,c4) <- verdad.
conectado(c4,c3) <- arriba(i3).
conectado(e1,c3) <- verdad.
conectado(c3,c5) <- está_bien(cc1).
conectado(e2,c6) <- verdad.
conectado(c6,c5) <- está_bien(cc2).
conectado(c5,entrada) <- verdad.

tiene_corriente(?D) se verifica si el dispositivo D tiene corriente.

tiene_corriente(D) <- 
   conectado(D,D1) &
   tiene_corriente(D1).
tiene_corriente(entrada) <- verdad.

está_encendida(?L) se verifica si la luz L está encendida.

está_encendida(L) <-
   luz(L) &
   está_bien(L) &
   tiene_corriente(L).

El código se encuentra en i_electrica.pl.

2. Metaintérpretes simples

2.1. Metaintéprete básico

prueba(+O) se verifica si el objetivo O se puede demostrar a partir de la base de conocimiento. Por ejemplo,

?- prueba(está_encendida(X)).
X = l2 ;
false.

Su definición es

prueba(verdad).
prueba((A & B)) :-
   prueba(A),
   prueba(B).
prueba(A) :-
   (A <- B),
   prueba(B).

Ejemplos de pruebas

?- [i_electrica].
true.

?- prueba(luz(l1)).
true 

?- prueba(luz(l6)).
false.

?- prueba(arriba(X)).
X = i2 ;
X = i3 ;
false.

?- prueba(conectado(l1,D)).
D = c0 ;
false.

?- prueba(conectado(c0,D)).
D = c1 ;
false.

?- prueba(conectado(c1,D)).
false.

?- prueba(conectado(D,c3)).
D = c2 ;
D = c4 ;
D = e1 ;
false.

?- prueba(conectado(X,Y)).
X = l1,
Y = c0 ;
X = c0,
Y = c1 ;
X = c2,
Y = c3 ;
X = l2,
Y = c4 ;
X = c4,
Y = c3 ;
X = e1,
Y = c3 ;
X = c3,
Y = c5 ;
X = e2,
Y = c6 ;
X = c6,
Y = c5 ;
X = c5,
Y = entrada ;
false.

?- prueba(tiene_corriente(D)).
D = c2 ;
D = l2 ;
D = c4 ;
D = e1 ;
D = c3 ;
D = e2 ;
D = c6 ;
D = c5 ;
D = entrada ;
false.

?- prueba(esta_encendida(X)).
X = l2 ;
false.

El código se encuentra en meta_simple.pl.

2.2. Metaintéprete ampliado

Ampliación del lenguaje base:
- Disyunciones: A ; B
- Predicados predefinidos: is, <, …

Operadores

:- op(1100, xfx, <-).
:- op(1000, xfy, [&,;]).

Base de conocimiento de vecinos
```
vecino(X,Y) <- Y is X-1 ; Y is X+1.
```
El código de la base de conocimiento de vecinos se encuentra en vecino.pl.

prueba(+O) se verifica si el objetivo O se puede demostrar a partir de la base de conocimiento (que puede contener disyunciones y predicados predefinidos). Por ejemplo,

?- [vecino].
true.
?- prueba(vecino(2,3)).
true.
?- prueba(vecino(3,2)).
true.

Su definición es

prueba(verdad).
prueba((A & B)) :- prueba(A), prueba(B).
prueba((A ; B)) :- prueba(A).
prueba((A ; B)) :- prueba(B).
prueba(A)       :- predefinido(A), A.
prueba(A)       :- (A <- B), prueba(B).

predefinido(+O) se verifica si O es un predicado predefinido.
```
predefinido((X is Y)).
predefinido((X < Y)).
```
El código del metaintéprete ampliado se encuentra en meta_ampliado.pl.

2.3. Metaintérprete con profundidad acotada

Ejemplo de base de conocimiento de hermandad:

hermano(X,Y) <- hermano(Y,X).
hermano(b,a) <- verdad.

El código de la base de conocimiento de hermandad se encuentra en hermano.pl.

Fallo al buscar la prueba con el metaintérprete simple.

?- [meta_simple].
true.

?- prueba(hermano(X,Y)).
ERROR: Stack limit (1.0Gb) exceeded

prueba_pa(+O,+N) es verdad si el objetivo O se puede demostrar con profundidad N como máximo. Por ejemplo,

?- [hermano].
true.

?- prueba_pa(hermano(a,X),1).
X = b ;
false.

?- prueba_pa(hermano(X,Y),1).
X = a,
Y = b ;
X = b,
Y = a ;
false.

?- prueba_pa(hermano(a,X),2).
X = b ;
false.

?- prueba_pa(hermano(a,X),3).
X = b ;
X = b ;
false.

Su definición es

prueba_pa(verdad,_N).
prueba_pa((A & B),N) :-
   prueba_pa(A,N),
   prueba_pa(B,N).
prueba_pa(A,N) :-
   N >= 0,
   N1 is N-1,
   (A <- B),
   prueba_pa(B,N1).

El código del metaintérprete con profundidad acotada se encuentra en meta_pa.pl.

Prueba con el metaintérprete simple usando call_with_depth_limit

?- call_with_depth_limit(prueba(hermano(X,Y)),1,R).
R = depth_limit_exceeded.

?- call_with_depth_limit(prueba(hermano(X,Y)),2,R).
X = b,
Y = a,
R = 3 ;
R = depth_limit_exceeded.

?- call_with_depth_limit(prueba(hermano(X,Y)),3,R).
X = a,
Y = b,
R = 4 ;
X = b,
Y = a,
R = 4 ;
false.

?- call_with_depth_limit(prueba(hermano(X,Y)),4,R).
X = b,
Y = a,
R = 5 ;
X = a,
Y = b,
R = 5 ;
X = b,
Y = a,
R = 4 ;
false.

3. Metaintérprete con preguntas

Ampliación de la base de conocimiento del sistema eléctrico.
```
preguntable(arriba(_)).
preguntable(abajo(_)).
```
El código de la base de conocimiento se encuentra en i_electrica_con_preguntas.pl.

prueba_p(+O) se verifica si el objetivo O se puede demostrar a partir de la BC objeto y las respuestas del usuario. Por ejemplo,

?- [i_electrica_con_preguntas, meta_con_preguntas].
true.

?- prueba_p(esta_encendida(L)).
¿Es verdad arriba(i2)? (si/no)
|: si.
¿Es verdad arriba(i1)? (si/no)
|: no.
¿Es verdad abajo(i2)? (si/no)
|: no.
¿Es verdad arriba(i3)? (si/no)
|: si.

L = l2 

?- listing(respuesta).
:- dynamic respuesta/2.

respuesta(arriba(i2), si).
respuesta(arriba(i1), no).
respuesta(abajo(i2), no).
respuesta(arriba(i3), si).

true.

?- retractall(respuesta(_,_)).
true.

?- prueba_p(esta_encendida(L)).
¿Es verdad arriba(i2)? (si/no)
|: si.
¿Es verdad arriba(i1)? (si/no)
|: si.

L = l1

Su definición es

prueba_p(verdad).
prueba_p((A & B)) :- 
   prueba_p(A), 
   prueba_p(B).
prueba_p(G) :-
   preguntable(G),
   respuesta(G,si).
prueba_p(G) :-
   preguntable(G),
   no_preguntado(G),
   pregunta(G,Respuesta),
   assert(respuesta(G,Respuesta)),
   Respuesta=si.
prueba_p(A) :-  
   (A <- B), 
   prueba_p(B).

respuesta(?O,?R) se verifica si la respuesta al objetivo O es R. (Se añade dinámicamente a la base de datos).
```
:- dynamic respuesta/2.
```
no_preguntado(+O) es verdad si el objetivo O no se ha preguntado.
```
no_preguntado(O) :-
   not(respuesta(O,_)).
```

pregunta(+O, -Respuesta) pregunta O al usuario y éste responde la Respuesta.

pregunta(O,Respuesta) :-
   escribe_lista(['¿Es verdad ',O,'? (si/no)']),
   read(Respuesta).

escribe_lista(+L) escribe cada uno de los elementos de la lista L.

escribe_lista([]) :- nl.
escribe_lista([X|L]) :-
   write(X),
   escribe_lista(L).

El código del metaintérprete con preguntas se encuentra en meta_con_preguntas.pl.

4. Metaintérprete con explicación

4.1. Metaintéprete con árbol de prueba

prueba_con_demostración((+O,?A) es verdad si A es un árbol de prueba del objetivo O. Por ejemplo,

?- [i_electrica].
true.

?- prueba_con_demostracion(está_encendida(L),T).
L = l2
T = si(está_encendida(l2),
        (si(luz(l2), verdad) &
         si(está_bien(l2), verdad) &
         si(tiene_corriente(l2),
             (si(conectado(l2, c4), verdad) &
              si(tiene_corriente(c4),
                  (si(conectado(c4, c3),
                       si(arriba(i3), verdad)) & 
                   si(tiene_corriente(c3),
                       (si(conectado(c3, c5),
                            si(está_bien(cc1), verdad)) &
                        si(tiene_corriente(c5),
                            (si(conectado(c5, entrada), verdad) &
                            si(tiene_corriente(entrada), verdad)))))))))))

Su definición es

prueba_con_demostración((verdad,verdad).
prueba_con_demostración(((A & B),(PA & PB)) :-
   prueba_con_demostración((A,PA),
   prueba_con_demostración((B,PB).
prueba_con_demostración((O,si(O,PB)) :-
   (O <- B),
   prueba_con_demostración((B,PB).

El código del metaintérprete con árbol de prueba se encuentra en meta_con_explicacion_arbol.pl.

4.2. Metaintérprete con explicación de cómo deduce.

prueba_con_explicación(+O) significa probar el objetivo O a partir de la base de conocimiento y navegar por su árbol de prueba mediante preguntas. Por ejemplo,

?- [i_electrica].
true.

?- prueba_con_explicación(está_encendida(L)).
está_encendida(l2) :-
   1: luz(l2)
   2: está_bien(l2)
   3: tiene_corriente(l2)
|: 3.
tiene_corriente(l2) :-
   1: conectado(l2, c4)
   2: tiene_corriente(c4)
|: 2.
tiene_corriente(c4) :-
   1: conectado(c4, c3)
   2: tiene_corriente(c3)
|: 1.
conectado(c4, c3) :-
   1: arriba(i3)
|: 1.
arriba(i3) es un hecho

L = l2

Su definición es

prueba_con_explicación(O) :-
   prueba_con_demostración((O,A),
   navega(A).

navega(+A) significa que se está navegando en el árbol A.

navega(si(A,verdad)) :-
    escribe_lista([A,' es un hecho']).
navega(si(A,B)) :-
    B \== verdad,
    escribe_lista([A,' :-']),
    escribe_cuerpo(B,1,_),
    read(Orden),
    interpreta_orden(Orden,B).

escribe_lista(+L) escribe cada uno de los elementos de la lista L.

escribe_lista([]) :- nl.
escribe_lista([X|L]) :-
   write(X),
   escribe_lista(L).

escribe_cuerpo(+B,+N1,?N2) es verdad si B es un cuerpo que se va a escribir, N1 es el número de átomos antes de la llamada a B y N2 es el número de átomos después de la llamada a B

escribe_cuerpo(verdad,N,N).
escribe_cuerpo((A & B),N1,N3) :-
   escribe_cuerpo(A,N1,N2),
   escribe_cuerpo(B,N2,N3).
escribe_cuerpo(si(H,_),N,N1) :-
   escribe_lista(['   ',N,': ',H]),
   N1 is N+1.

interpreta_orden(+Orden,+B) interpreta la Orden sobre el cuerpo B.

interpreta_orden(N,B) :-
   integer(N),
   nth(B,N,E),
   navega(E).

nth(+E,+N,?A) es verdad si A es el N-ésimo elemento de la estructura E

nth(A,1,A) :-
   not((A = (_,_))).
nth((A&_),1,A).
nth((_&B),N,E) :-
   N>1,
   N1 is N-1,
   nth(B,N1,E).

El código del metaintérprete con explicaciones de cómo se encuentra en meta_con_explicacion_como.pl.

4.3. Metaintérprete con explicación de por qué plantea una pregunta

prueba_con_porque(O) significa probar el objetivo O, con las respuestas del usuario, permitiéndole preguntar por qué se le plantean preguntas. Por ejemplo,

?- [i_electrica_con_preguntas].
true.

?- prueba_con_porque(esta_encendida(L)).
¿Es verdad arriba(i2)? (si/no/porque)
|: porque.
Se usa en:
   conectado(c0,c1) <- 
       arriba(i2).
¿Es verdad arriba(i2)? (si/no/porque)
|: porque.
Se usa en:
   tiene_corriente(c0) <- 
       conectado(c0,c1) &
       tiene_corriente(c1).
¿Es verdad arriba(i2)? (si/no/porque)
|: porque.
Se usa en:
   tiene_corriente(l1) <- 
       conectado(l1,c0) &
       tiene_corriente(c0).
¿Es verdad arriba(i2)? (si/no/porque)
|: porque.
Se usa en:
   esta_encendida(l1) <- 
       luz(l1) &
       esta_bien(l1) &
       tiene_corriente(l1).
¿Es verdad arriba(i2)? (si/no/porque)
|: porque.
Porque esa fue su pregunta!
¿Es verdad arriba(i2)? (si/no/porque)
|: si.
¿Es verdad arriba(i1)? (si/no/porque)
|: porque.
Se usa en:
   conectado(c1,c3) <- 
       arriba(i1).
¿Es verdad arriba(i1)? (si/no/porque)
|: no.
¿Es verdad abajo(i2)? (si/no/porque)
|: porque.
Se usa en:
   conectado(c0,c2) <- 
       abajo(i2).
¿Es verdad abajo(i2)? (si/no/porque)
|: si.
¿Es verdad abajo(i1)? (si/no/porque)
|: si.

L = l1

Su definición es

prueba_con_porque(O) :-
   prueba_con_porque_aux(O,[]).

prueba_con_porque_aux(O,Antecesores) se verifica si O es probable con la lista de Antecesores. Pregunta al usuario y las posibles respuesta son Sí, No o Por qué hace la pregunta.

prueba_con_porque_aux(verdad,_).
prueba_con_porque_aux((A & B), Antecesores) :-
   prueba_con_porque_aux(A,Antecesores),
   prueba_con_porque_aux(B,Antecesores).
prueba_con_porque_aux(O,_) :-
   preguntable(O),
   respuesta(O,si).
prueba_con_porque_aux(O,Antecesores) :-
   preguntable(O),
   no_preguntado(O),
   pregunta(O,Respuesta,Antecesores),
   assert(respuesta(O,Respuesta)),
   Respuesta=si.
prueba_con_porque_aux(A,Antecesores) :-
   (A <- B),
   prueba_con_porque_aux(B,[(A <- B)|Antecesores]).

respuesta(O,Respuesta) se añade dinámicamente a la base de datos.
```
:- dynamic respuesta/2.
```
no_preguntado(O) se verifica si el objetivo O no se ha preguntado.
```
no_preguntado(G) :- \+ respuesta(G,_).   
```

pregunta(O,Respuesta,Antecesores) pregunta al usuario, en el contexto dado por los Antecesores, la cuestión O y éste escribe la Respuesta.

pregunta(O,Respuesta,Antecesores) :-
   escribe_lista(['¿Es verdad ',O,'? (si/no/porque)']),
   read(Replica),
   interpreta(O,Respuesta,Replica,Antecesores).

escribe_lista(L) escribe cada uno de los elementos de la lista L.

escribe_lista([]) :- nl.
escribe_lista([X|L]) :-
   write(X),
   escribe_lista(L).

interpreta(O,Respuesta,Replica,Antecesores) interpreta la Replica (cuyos posibles valores son si, no o porque) en el contexto de los Antecesores.

interpreta(_,Replica,Replica,_) :-
   Replica \== porque.
interpreta(O,Respuesta,porque,[Regla|Reglas]):-
   write('Se usa en:'), nl,
   escribe_regla(Regla),
   pregunta(O,Respuesta,Reglas).
interpreta(O,Respuesta,porque,[]):-
   write('Porque esa fue su pregunta!'), nl,
   pregunta(O,Respuesta,[]).

escribe_regla(R) escribe la regla R.

escribe_regla((A <- B)) :-
   escribe_lista(['   ',A, ' <- ']),
   escribe_cuerpo(B).

escribe_cuerpo(C) escribe el cuerpo C de una regla.

escribe_cuerpo((A & B)) :-
   escribe_lista(['       ',A, ' &']),
   escribe_cuerpo(B).
escribe_cuerpo(A) :-
   \+ A = (_B & _C),
   escribe_lista(['       ',A,'.']).

El código del metaintérprete con explicaciones de por qué se encuentra en meta_con_explicacion_porque.pl.

5. Bibliografía

T. Cornell. Introduction to Prolog. (Universität Tübingen, 1998).
- Cap. 12: Metaleanguage, metalogic an metaprogramming.
- Cap. 13: Prolog as an assembler for logic programming systems.
D. Poole, A. Mackworth y R. Goebel. Computational intelligence (A logical approach). (Oxford University Press, 1998)
- Cap. 5: Knowledge engineering.
Y. Shoham. Artificial intelligence techniques in Prolog. (Morgan Kaufmann, 1994).
- Cap. 3: Backward-chaining methods.
M. Triska A couple of meta-interpreters in Prolog.