Tema 3: Estructuras
Índice
1. Segmentos verticales y horizontales
- Nota: El código del programa que se desarrollará en esta sección se encuentra en ver_hor.pl.
1.1. Representación de puntos y segmentos
punto(X,Y)representa el punto de coordenadas(X,Y).seg(P1,P2)representa el segmento cuyos extremos son los puntosP1yP2.
1.2. Segmentos horizontales y verticales
Relaciones:
horizontal(S)se verifica si el segmentoSes horizontal.vertical(S)se verifica si el segmentoSes vertical. Por ejemplo,
?- vertical(seg(punto(1,1),punto(1,2))). true. ?- vertical(seg(punto(1,1),punto(2,2))). false. ?- horizontal(seg(punto(1,2),punto(1,3))). false. ?- horizontal(seg(punto(1,2),punto(4,2))). true.
Programa:
horizontal(seg(punto(_,Y),punto(_ ,Y))). vertical(seg(punto(X,_),punto(X,_ ))).
1.3. Consultas sobre segmentos
¿Es vertical el segmento que une los puntos
(1,1)y(1,2)??- vertical(seg(punto(1,1),punto(1,2))). true.
¿Es vertical el segmento que une los puntos
(1,1)y(2,2)??- vertical(seg(punto(1,1),punto(2,2))). false.
¿Hay algún
Ytal que el segmento que une los puntos(1,1)y(2,Y)sea vertical??- vertical(seg(punto(1,1),punto(2,Y))). false.
¿Hay algún
Xtal que el segmento que une los puntos(1,2)y(X,3)sea vertical??- vertical(seg(punto(1,2),punto(X,3))). X = 1.
¿Hay algún
Ytal que el segmento que une los puntos(1,1)y(2,Y)sea horizontal??- horizontal(seg(punto(1,1),punto(2,Y))). Y = 1.
¿Para qué puntos el segmento que comienza en
(2,3)es vertical??- vertical(seg(punto(2,3),P)). P = punto(2, _2328).
¿Hay algún segmento que sea horizontal y vertical?
?- vertical(S),horizontal(S). S = seg(punto(_3356, _3358), punto(_3356, _3358)). ?- vertical(_),horizontal(_). true.
2. Base de dato de familias.
- Nota: El código del programa que se desarrollará en esta sección se encuentra en familia.pl.
2.1. Representación de las familia
- Descripción de la familia 1 :
- el padre es Tomás García Pérez, nacido el 7 de Mayo de 1970, trabaja de profesor y gana 75 euros diarios
- la madre es Ana López Ruiz, nacida el 10 de marzo de 1972, trabaja de médica y gana 100 euros diarios
- el hijo es Juan García López, nacido el 5 de Enero de 1990, estudiante
- la hija es María García López, nacida el 12 de Abril de 1992, estudiante
Representación de la familia 1:
familia(persona([tomas,garcia,perez], fecha(7,mayo,1990), trabajo(profesor,75)), persona([ana,lopez,ruiz], fecha(10,marzo,1972), trabajo(medica,100)), [ persona([juan,garcia,lopez], fecha(5,enero,1990), estudiante), persona([maria,garcia,lopez], fecha(12,abril,1992), estudiante) ]).
- Descripción de la familia 2:
- el padre es José Pérez Ruiz, nacido el 6 de Marzo de 1973, trabaja de pintor y gana 150 euros/día
- la madre es Luisa Gálvez Pérez, nacida el 12 de Mayo de 1974, es médica y gana 100 euros/día
- un hijo es Juan Luis Pérez Pérez, nacido el 5 de Febrero de 2000, estudiante
- una hija es María José Pérez Pérez, nacida el 12 de Junio de 2002, estudiante
- otro hijo es José María Pérez Pérez, nacido el 12 de Julio de 2004, estudiante
Representación de la familia 2:
familia(persona([jose,perez,ruiz], fecha(6,marzo,1973), trabajo(pintor,150)), persona([luisa,galvez,perez], fecha(12,mayo,1974), trabajo(medica,100)), [ persona([juan_luis,perez,perez], fecha(5,febrero,2000), estudiante), persona([maria_jose,perez,perez], fecha(12,junio,2002), estudiante), persona([jose_maria,perez,perez], fecha(12,julio,2004), estudiante) ]).
2.2. Consultas sobre las familias
¿Existe alguna familia sin hijos?
?- familia(_,_,[]). false.
¿Existe alguna familia con tres hijos?
?- familia(_,_,[_,_,_]). true.
¿Existe alguna familia con cuatro hijos?
?- familia(_,_,[_,_,_,_]). false.
Buscar los nombres de los padres de familia con tres hijos
?- familia(persona(NP,_,_),_,[_,_,_]). NP = [jose, perez, ruiz] ; false.
2.3. Ampliación con los hombres casados
casado(X)se verifica siXes un hombre casado.casado(X) :- familia(X,_,_).
Consulta:
?- casado(X). X = persona([tomas, garcia, perez], fecha(7, mayo, 1990), trabajo(profesor, 75)) ; X = persona([jose, perez, ruiz], fecha(6, marzo, 1973), trabajo(pintor, 150)) ; false.
2.4. Ampliación con las mujeres casadas
casada(X)se verifica siXes una mujer casada.casada(X) :- familia(_,X,_).
Consulta:
?- casada(X). X = persona([ana, lopez, ruiz], fecha(10, marzo, 1972), trabajo(medica, 100)) ; X = persona([luisa, galvez, perez], fecha(12, mayo, 1974), trabajo(medica, 100)) ; false.
2.5. Preguntas compuestas
Buscar los nombres de las mujeres casadas que trabajan
?- casada(persona([N,_,_],_,trabajo(_,_))). N = ana ; N = luisa ; false.
2.6. Resumen de conceptos introducidos
- Uso de objetos estructurados.
- Prolog como lenguaje de consulta de bases de datos.
- Bases de datos como conjuntos de hechos.
- Selectores.
- Abstracción de datos.
3. Simulación de un autómata
- Nota: El código del programa que se desarrollará en esta sección se encuentra en automata.pl.
3.1. Representación del autómata
- Autómata no determinista (con estado final
e3):
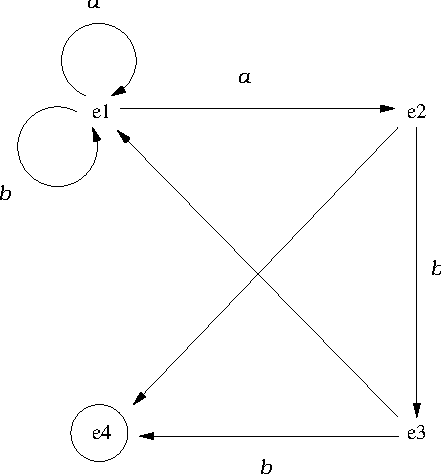
final(E)se verifica siEes el estado final.final(e3).
trans(E1,X,E2)se verifica si se puede pasar del estadoE1al estadoE2usando la letraXtrans(e1,a,e1). trans(e1,a,e2). trans(e1,b,e1). trans(e2,b,e3). trans(e3,b,e4).
nulo(E1,E2)se verifica si se puede pasar del estadoE1al estadoE2mediante un movimiento nulo.nulo(e2,e4). nulo(e3,e1).
acepta(E,L)se verifica si el autómata, a partir del estadoEacepta la listaL. Por ejemplo,?- acepta(e1,[a,a,a,b]). true ; false. ?- acepta(e2,[a,a,a,b]). false.
Su definición es
acepta(E,[]) :- final(E). acepta(E,[X|L]) :- trans(E,X,E1), acepta(E1,L). acepta(E,L) :- nulo(E,E1), acepta(E1,L).
3.2. Consultas sobre el autómata
Determinar si el autómata acepta la lista
[a,a,a,b]?- acepta(e1,[a,a,a,b]). true ; false.
Determinar los estados a partir de los cuales el autómata acepta la lista
[a,b]?- acepta(E,[a,b]). E=e1 ; E=e3 ; false.
Determinar las palabras de longitud 3 aceptadas por el autómata a partir del estado
e1?- acepta(e1,[X,Y,Z]). X = Y, Y = a, Z = b ; X = Z, Z = b, Y = a ;
4. Problema del mono
- Nota: El código del programa que se desarrollará en esta sección se encuentra en mono.pl.
4.1. Descripción del problema del mono
- Descripción: Un mono se encuentra en la puerta de una habitación. En el centro de la habitación hay un plátano colgado del techo. El mono está hambriento y desea coger el plátano, pero no lo alcanza desde el suelo. En la ventana de la habitación hay una silla que el mono puede usar. El mono puede realizar las siguientes acciones: pasear de un lugar a otro de la habitación, empujar la silla de un lugar a otro de la habitación (si está en el mismo lugar que la silla), subirse en la silla (si está en el mismo lugar que la silla) y coger el plátano (si está encima de la silla en el centro de la habitación).
4.2. Representación de los estados
estado(PM,AM,PS,MM)es el estado tal quePMes la posición del mono (sus valores sonpuerta,centrooventana)AMes el apoyo del mono (sus valores sonsueloosilla).PSes la posición de la silla (sus valores sonpuerta,centrooventana).MMindica si la mano del mono tiene el plátano (sus valores sonconosin).
4.3. Acciones y movimientos
movimiento(E1,A,E2)se verifica siE2es el estado que resulta de realizar la acciónAen el estadoE1movimiento(estado(centro,silla,centro,sin), coger, estado(centro,silla,centro,con)). movimiento(estado(X,suelo,X,U), subir, estado(X,silla,X,U)). movimiento(estado(X1,suelo,X1,U), empujar(X1,X2), estado(X2,suelo,X2,U)). movimiento(estado(X,suelo,Z,U), pasear(X,Z), estado(Z,suelo,Z,U)).
4.4. Solución del problema del mono
solución(E,S)se verifica siSes una sucesión de acciones que aplicadas al estadoEpermiten al mono coger el plátano. Por ejemplo,?- solución(estado(puerta,suelo,ventana,sin),L). L = [pasear(puerta, ventana), empujar(ventana, centro), subir, coger]
Su definición es
solución(estado(_,_,_,con),[]). solución(E1,[A|L]) :- movimiento(E1,A,E2), solución(E2,L).
- La representación de la búsqueda de soluciones es
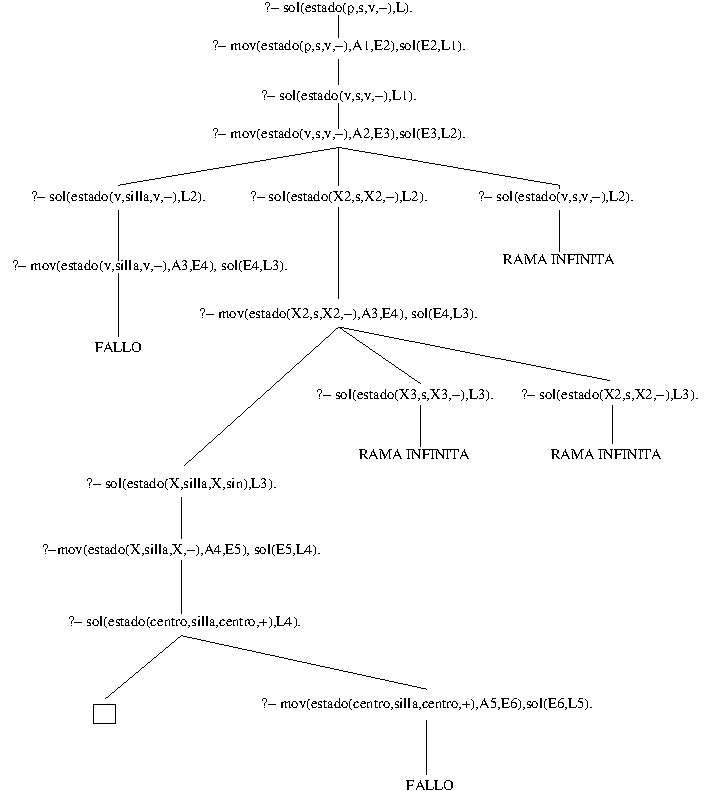
5. Ejercicios
5.1. Ampliación del programa de las familias
Ejercicio 1. En este ejercicio vamos a considerar el programa familia.pl del
tema 3 que se incluye a continuación
familia(persona([tomás,garcía,pérez], fecha(7,mayo,1990), trabajo(profesor,75)), persona([ana,lópez,ruiz], fecha(10,marzo,1972), trabajo(médica,100)), [ persona([juan,garcía,lópez], fecha(5,enero,1990), estudiante), persona([maría,garcía,lópez], fecha(12,abril,1992), estudiante) ]). familia(persona([josé,pérez,ruiz], fecha(6,marzo,1973), trabajo(pintor,150)), persona([luisa,gálvez,pérez], fecha(12,mayo,1974), trabajo(médica,100)), [ persona([juan_luis,pérez,pérez], fecha(5,febrero,2000), estudiante), persona([maría_josé,pérez,pérez], fecha(12,junio,2002), estudiante), persona([josé_maría,pérez,pérez], fecha(12,julio,2004), estudiante) ]). casado(X) :- familia(X,_,_). casada(X) :- familia(_,X,_).
Ejercicio 1.1. Definir la relación hijo(X) que se verifique si X figura en
alguna lista de hijos.
Solución
hijo(X) :- familia(_,_,L), member(X,L).
Ejercicio 1.2. Calcular los hijos de las familias.
Solución
?- hijo(X). X = persona([juan, garcía, lópez], fecha(5, enero, 1990), estudiante) ; X = persona([maría, garcía, lópez], fecha(12, abril, 1992), estudiante) ; X = persona([juan_luis, pérez, pérez], fecha(5, febrero, 2000), estudiante) ; X = persona([maría_josé, pérez, pérez], fecha(12, junio, 2002), estudiante) ; X = persona([josé_maría, pérez, pérez], fecha(12, julio, 2004), estudiante).
Ejercicio 1.3. Definir la relación existe(X) que se verifique si X es una
persona existente en la base de datos.
Solución
existe(X) :- casado(X); casada(X); hijo(X).
Ejercicio 1.4. Hacer una pregunta tal que que las respuestas sean las listas de la forma [nombre, apellido1, apellido2] de todas las personas que existen en las familias.
Solución
?- existe(persona(X,_,_)). X = [tomás, garcía, pérez] ; X = [josé, pérez, ruiz] ; X = [ana, lópez, ruiz] ; X = [luisa, gálvez, pérez] ; X = [juan, garcía, lópez] ; X = [maría, garcía, lópez] ; X = [juan_luis, pérez, pérez] ; X = [maría_josé, pérez, pérez] ; X = [josé_maría, pérez, pérez].
Ejercicio 1.5. Determinar todos los estudiantes nacidos antes de 2003.
Solución
?- existe(persona(X,fecha(_,_,Año),estudiante)), Año < 2003. X = [juan, garcía, lópez], Año = 1990 ; X = [maría, garcía, lópez], Año = 1992 ; X = [juan_luis, pérez, pérez], Año = 2000 ; X = [maría_josé, pérez, pérez], Año = 2002 ; false.
Ejercicio 1.6. Definir la relación fecha_de_nacimiento(X,Y) de forma que si
X es una persona, entonces Y es su fecha de nacimiento.
Solución
fecha_de_nacimiento(persona(_,Y,_),Y).
Ejercicio 1.7. Buscar todos los hijos nacidos en 2002.
Solución
?- hijo(X), fecha_de_nacimiento(X,fecha(_,_,2002)). X = persona([maría_josé, pérez, pérez], fecha(12, junio, 2002), estudiante) false.
Ejercicio 1.8. Definir la relación sueldo(X,Y) que se verifique si el sueldo
de la persona X es Y.
Solución
sueldo(persona(_,_,trabajo(_,Y)),Y). sueldo(persona(_,_,estudiante),0).
Ejercicio 1.9. Buscar todas las personas nacidas antes de 1974 cuyo sueldo sea superior a 72 euros.
Solución
?- existe(X), fecha_de_nacimiento(X,fecha(_,_,Año)), Año < 1974, sueldo(X,Y), Y > 72. X = persona([josé, pérez, ruiz], fecha(6, marzo, 1973), trabajo(pintor, 150)), Año = 1973, Y = 150 ; X = persona([ana, lópez, ruiz], fecha(10, marzo, 1972), trabajo(médica, 100)), Año = 1972, Y = 100 ; false.
Ejercicio 1.10. Definir la relación total(L,Y) que se verifique si Y es la
suma de los sueldos de las personas de la lista L.
Solución
total([],0). total([X|L],Y) :- sueldo(X,Y1), total(L,Y2), Y is Y1 + Y2.
Ejercicio 1.11. Calcular los ingresos totales de cada familia.
Solución
?- familia(X,Y,Z), total([X,Y|Z],Total). X = persona([tomás, garcía, pérez], fecha(7, mayo, 1990), trabajo(profesor, 75)), Y = persona([ana, lópez, ruiz], fecha(10, marzo, 1972), trabajo(médica, 100)), Z = [persona([juan, garcía, lópez], fecha(5, enero, 1990), estudiante), persona([maría, garcía, lópez], fecha(12, abril, 1992), estudiante)], Total = 175 ; X = persona([josé, pérez, ruiz], fecha(6, marzo, 1973), trabajo(pintor, 150)), Y = persona([luisa, gálvez, pérez], fecha(12, mayo, 1974), trabajo(médica, 100)), Z = [persona([juan_luis, pérez, pérez], fecha(5, febrero, 2000), estudiante), persona([maría_josé, pérez, pérez], fecha(12, junio, 2002), estudiante), persona([josé_maría, pérez, pérez], fecha(12, julio, 2004), estudiante)], Total = 250 ; false.
5.2. Ampliación de simulación de autómata
Ejercicio 2. En este ejercicio consideraremos el programa automata.pl
del tema 3 que se incluye a continuación.
Solución
final(e3). trans(e1,a,e1). trans(e1,a,e2). trans(e1,b,e1). trans(e2,b,e3). trans(e3,b,e4). nulo(e2,e4). nulo(e3,e1).
Ejercicio 2.1. Definir la relación acepta_acotada(E,L,N) que se verifique si
el autómata, a partir del estado E, acepta la lista L y la longitud de L
es N.
1ª solución
acepta_acotada_a(E,L,N) :- length(L,N), acepta_acotada_a_aux(E,L). acepta_acotada_a_aux(E,[]) :- final(E). acepta_acotada_a_aux(E,[X|L]) :- trans(E,X,E1), acepta_acotada_a_aux(E1,L). acepta_acotada_a_aux(E,L) :- nulo(E,E1), acepta_acotada_a_aux(E1,L).
2ª solución
acepta_acotada_b(E,[],0) :- final(E). acepta_acotada_b(E,[X|L],N) :- N > 0, trans(E,X,E1), M is N -1, acepta_acotada_b(E1,L,M). acepta_acotada_b(E,L,N) :- nulo(E,E1), acepta_acotada_b(E1,L,N).
Ejercicio 2.2. Buscar las cadenas aceptadas a partir de e1 con longitud 3.
Solución
?- acepta_acotada_a(e1,L,3). L = [a, a, b] ; L = [b, a, b] ; false. ?- acepta_acotada_b(e1,L,3). L = [a, a, b] ; L = [b, a, b] ; false.
Ejercicio 2.3. Definir la relación acepta_acotada_2(E,L,N) que se verifique
si el autómata, a partir del estado E, acepta la lista L y la longitud de
L es menor o igual que N.
1ª solución
acepta_acotada_2_a(E,L,N) :- between(0,N,M), length(L,M), acepta_acotada_a_aux(E,L).
2ª solución
acepta_acotada_2_b(E,[],_N) :- final(E). acepta_acotada_2_b(E,[X|L],N) :- N > 0, trans(E,X,E1), M is N-1, acepta_acotada_2_b(E1,L,M). acepta_acotada_2_b(E,L,N) :- nulo(E,E1), acepta_acotada_2_b(E1,L,N).
Ejercicio 2.4. Buscar las cadenas aceptadas a partir de e1 con longitud
menor o igual que 3.
Solución
?- acepta_acotada_2_a(e1,L,3). L = [a, b] ; L = [a, a, b] ; L = [b, a, b] ; false. ?- acepta_acotada_2_b(e1,L,3). L = [a, a, b] ; L = [a, b] ; L = [b, a, b] ; false.
5.3. Rompecabeza de la banda de música
Ejercicio 3. Se sabe que
- Una banda está compuesta por tres músicos de distintos paises y que tocan distintos instrumentos.
- El pianista toca primero.
- Juan toca el saxo y toca antes que el australiano.
- Marcos es francés y toca antes que el violinista.
- Hay un músico japonés.
- Un músico se llama Saúl.
Determinar el nombre, el país y el instrumento que toca cada uno de los músicos de la banda.
Solución
La relación solución_músicos(S) se verifica si S es una solución del
problema de los músicos.
solución_músicos(S) :- % 1. Una banda está compuesta por tres músicos de distintos paises % y que tocan distintos instrumentos. presolución(S), % 2. El pianista toca primero. instrumento(X,piano), primero(X,S), % 3. Juan toca el saxo y toca antes que el australiano. nombre(Y,juan), instrumento(Y,saxo), país(Z,australia), antes(Y,Z,S), % 4. Marcos es francés y toca antes que el violinista. nombre(Y1,marco), país(Y1,francia), instrumento(Z1,violín), antes(Y1,Z1,S), % 5. Hay un músico japonés. pertenece(U,S), país(U,japón), % 6. Un músico se llama Saúl. pertenece(V,S), nombre(V,saúl).
La definición se basa en relación presolución(S)4 que se verifica si ~S
es una presolución; i.e. S es un término de la forma
banda(músico(N1,P1,I1),
músico(N2,P2,I2),
músico(N3,P3,I3))
donde músico(N,P,I) representa al músico de nombre N, país P y que toca el
instrumento I.
presolución(banda(músico(_N1,_P1,_I1), músico(_N2,_P2,_I2), músico(_N3,_P3,_I3))).
Además, se usan las siguientes relaciones auxiliares:
nombre(X,N)se verifica siN4 es el el nombre del músico ~X.nombre(músico(N,_,_),N).
país(X,P)se verifica siPes el país del músicoX.país(músico(_,P,_),P).
instrumento(X,I)se verifica siIes el instrumento que toca el músicoX.instrumento(músico(_,_,I),I).
primero(X,B)se verifica siXes el primer músico de la bandaB.primero(X,banda(X,_,_)).
pertenece(X,B)se verifica siXes un músico de la bandaB.pertenece(X,banda(X,_,_)). pertenece(X,banda(_,X,_)). pertenece(X,banda(_,_,X)).
antes(X,Y,B)se verifica siXtoca antes queYen la bandaB.antes(X,Y,banda(X,Y,_)). antes(X,Y,banda(X,_,Y)). antes(X,Y,banda(_,X,Y)).
La consulta para obtener la solución es
?- solución_músicos(S). S = [músico(marco, francia, piano), músico(juan, japón, saxo), músico(saúl, australia, violín)] ; false.
5.4. Recorrido del caballo de ajedrez
Ejercicio 4.1. Supongamos que los cuadros del tablero de ajedrez los
representamos por pares de números [X,Y] con X e Y entre 1 y 8.
Definir la relación salta(+C1,?C2) que se verifica si el
caballo puede pasar en un movimiento del cuadrado C1 al cuadrado
C2. Por ejemplo,
?- salta([1,1],S). S = [3, 2] ; S = [2, 3] ; false.
Solución
salta([X,Y],[X1,Y1]) :- dxy(Dx,Dy), X1 is X+Dx, correcto(X1), Y1 is Y+Dy, correcto(Y1). % dxy(?X,?Y) se verifica si un caballo puede moverse X espacios % horizontales e Y verticales. dxy(2,1). dxy(2,-1). dxy(-2,1). dxy(-2,-1). dxy(1,2). dxy(1,-2). dxy(-1,2). dxy(-1,-2). % correcto(+X) se verifica si X está entre 1 y 8. correcto(X) :- 1 =< X, X =< 8.
Ejercicio 4.2. Definir la relación camino(L) que se verifica si L es
una lista de cuadrados representando el camino recorrido por un
caballo sobre un tablero vacío. Por ejemplo,
?- camino([[1,1],C]). C = [3, 2] ; C = [2, 3] ; false.
Solución
camino([_]). camino([C1,C2|L]) :- salta(C1,C2), camino([C2|L]).
Ejercicio 4.3. Usando la relación camino, escribir una pregunta para
determinar los caminos de longitud 4 por los que puede desplazarse un caballo
desde cuadro [2,1] hasta el otro extremo del tablero (Y=8) de forma que en el
segundo movimiento pase por el cuadro [5,4].
Solución
?- camino([[2,1],C1,[5,4],C2,[X,8]]). C1 = [4, 2], C2 = [6, 6], X = 7 ; C1 = [4, 2], C2 = [6, 6], X = 5 ; C1 = [4, 2], C2 = [4, 6], X = 5 ; C1 = [4, 2], C2 = [4, 6], X = 3 ; C1 = [3, 3], C2 = [6, 6], X = 7 ; C1 = [3, 3], C2 = [6, 6], X = 5 ; C1 = [3, 3], C2 = [4, 6], X = 5 ; C1 = [3, 3], C2 = [4, 6], X = 3 ;
Ejercicio 4.4. Calcular el menor número de movimientos necesarios para desplazar el caballo del cuadro [1,1] al [2,2]. ¿Cuántos caminos de dicha longitud hay de [1,1] a [2,2]?
Solución
?- camino([[1,1],_,[2,2]]). false. ?- camino([[1,1],_,_,[2,2]]). false. ?- camino([[1,1],_,_,_,[2,2]]). true ?- camino([[1,1],C2,C3,C4,[2,2]]). C2 = [3, 2], C3 = [5, 3], C4 = [3, 4] ; C2 = [3, 2], C3 = [5, 3], C4 = [4, 1] ; C2 = [3, 2], C3 = [5, 1], C4 = [4, 3] ; C2 = [3, 2], C3 = [1, 3], C4 = [3, 4] ; C2 = [3, 2], C3 = [2, 4], C4 = [4, 3] ; C2 = [2, 3], C3 = [4, 2], C4 = [3, 4] ; C2 = [2, 3], C3 = [3, 5], C4 = [1, 4] ; C2 = [2, 3], C3 = [3, 5], C4 = [4, 3] ; C2 = [2, 3], C3 = [3, 1], C4 = [4, 3] ; C2 = [2, 3], C3 = [1, 5], C4 = [3, 4] ; false.
5.5. Máximo de un árbol binario
Ejercicio 5. Un árbol binario es vacío o consta de tres partes: la raíz (que debe de ser un número positivo), el subárbol izquierdo (que debe ser un árbol binario) y el subárbol derecho (que debe ser un árbol binario). Usaremos la siguiente representación
nilrepresenta el árbol vacíot(I,R,D)representa el árbol de la raízR, subárbol izquierdoIy subárbol derechoD.
Por ejemplo, el término t(t(nil,2,nil),1,t(t(nil,4,nil),3,nil))
representa el árbol
1
/ \
2 3
/
4
Definir la relación máximo(+T,-X) que se verifica si X es el máximo
de los nodos del árbol T. Por ejemplo,
?- máximo(nil,N). N = 0. ?- máximo(t(nil,2,nil),N). N = 2. ?- máximo(t(t(nil,2,nil),3,nil),N). N = 3.
Solución
máximo(nil,0). máximo(t(I,R,D),M):- máximo(I,MI), máximo(D,MD), M1 is max(MI,MD), M is max(R,M1).
6. Bibliografía
- I. Bratko
Prolog programming for artificial intelligence (3 ed.)
(Addison–Wesley, 2001)
- Cap. 2: "Syntax and meaning of Prolog programs".
- Cap. 4: "Using structures: Example programs"
- W.F. Clocksin y C.S. Mellish
Programming in Prolog.
(Springer Verlag, 1994)
- Cap. 3: "Using data structures"
- T. Cornell.
Introduction to Prolog.
(Universität Tübingen, 1998).
- Cap. 5.5: Finite state automata.
- Cap. 6: Trees.
- J.M. Spivey
Introduction to logic programming through Prolog.
(Prentice-Hall International, 1996).
- Cap. 3: Recursive structures.
- T. Van Le
Techniques of Prolog programming.
(John Wiley, 1993)
- Cap. 2: "Declarative Prolog programming".