Tema 4: Retroceso, corte y negación
Índice
- 1. Control mediante corte
- 2. Negación como fallo
- 3. El condicional
- 4. Ejercicios
- 4.1. Diferencia de conjuntos
- 4.2. Agregación de elementos a conjuntos
- 4.3. Separación de positivos de no positivos
- 4.4. Suma de los números pares
- 4.5. Exponente de 2 en la factorización prima
- 4.6. Uso y variante de concatenación para calcular prefijo
- 4.7. Signos de crecimientos de sucesiones numéricas
- 4.8. Descomposición en factores primos
- 4.9. Menor múltiplo con suma de sus dígitos mayor que N
- 4.10. Números libres de cuadrados
- 4.11. Suma de los números libres de cuadrados
- 4.12. Longitud de las subsucesiones comunes maximales
- 4.13. Elementos repetidos en una lista
- 4.14. Subconjunto maximal
- 4.15. Suma de los elementos con posiciones múltiplos de n
- 4.16. Compresión de listas
- 4.17. Empaquetamiento de listas
- 4.18. Codificación por longitud
- 4.19. Codificación reducida por longitud
- 4.20. Decodificación de lista
- 4.21. Dientes de sierra
- 5. Bibliografía
1. Control mediante corte
1.1. Ejemplo de nota sin corte:
nota(X,Y)se verifica siYes la calificación correspondiente a la notaX; es decir,YessuspensosiXes menor que5,YesaprobadosiXes mayor o igual que5pero menor que7,YesnotablesiXes mayor que7pero menor que9eYes sobresaliente siXes mayor que9.Definición notas_1.pl
nota(X,suspenso) :- X < 5. nota(X,aprobado) :- X >= 5, X < 7. nota(X,notable) :- X >= 7, X < 9. nota(X,sobresaliente) :- X >= 9.
Ejemplo: ¿cuál es la calificación correspondiente a un
6?:?- nota(6,Y). Y = aprobado ; false.
- Árbol de deducción de
?- nota(6,Y).
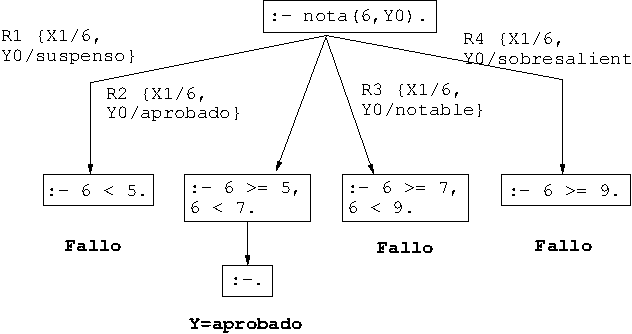
1.2. Ejemplo de nota con cortes
Definición (notas_2.pl).
nota(X,suspenso) :- X < 5, !. nota(X,aprobado) :- X < 7, !. nota(X,notable) :- X < 9, !. nota(X,sobresaliente).
¿Cuál es la calificación correspondiente a un
6?:?- nota(6,X). X = aprobado.
- Árbol de deducción de
?- nota(6,Y).
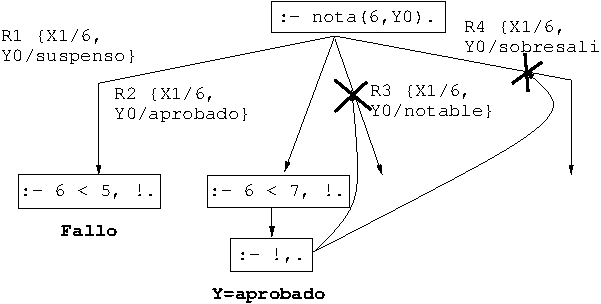
Ejemplo: ¿Es
6sobresaliente?:?- nota(6,sobresaliente). true.
1.3. Uso de corte para respuesta única
Diferencia entre
memberymemberchk?- member(X,[a,b,a,c]), X = a. X = a ; X = a ; false. ?- memberchk(X,[a,b,a,c]), X = a. X = a.
Definición de
memberymemberchk:member(X,[X|_]). member(X,[_|L]) :- member(X,L). memberchk(X,[X|_]) :- !. memberchk(X,[_|L]) :- memberchk(X,L).
2. Negación como fallo
2.1. Definición de la negación como fallo
Definición de la negación como fallo (
not):no(P) :- P, !, fail. % false. 1 no(_). % false. 2
Programa con negación (aprobados_1.pl).
aprobado(X) :- no(suspenso(X)), matriculado(X). % R1 matriculado(juan). % R2 matriculado(luis). % R3 suspenso(juan). % R4
Consultas:
?- aprobado(luis). true. ?- aprobado(X). false.
- Árbol de deducción de
?- aprobado(luis).:
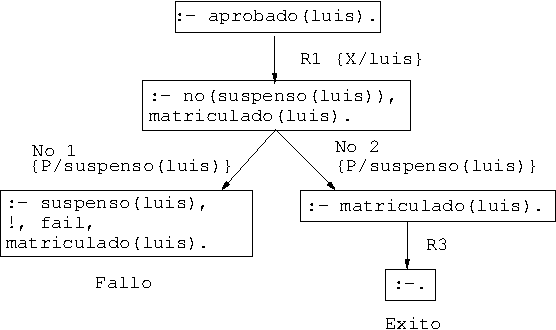
- Árbol de deducción de
?- aprobado(X).
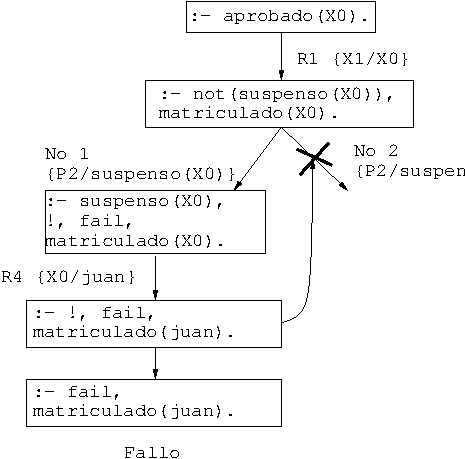
- Modificación del orden de los literales
Programa (aprobados_2.pl)
aprobado(X) :- matriculado(X), no(suspenso(X)). % R1 matriculado(juan). % R2 matriculado(luis). % R3 suspenso(juan). % R4
Consulta:
?- aprobado(X). X = luis.
- Árbol de deducción de
?- aprobado(X).
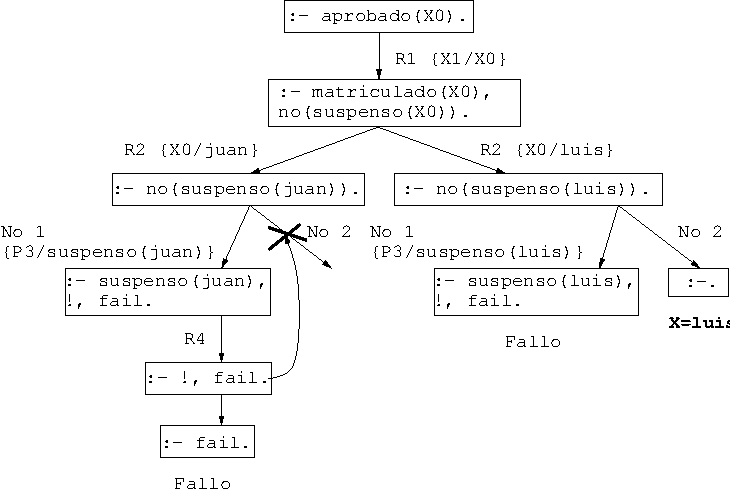
2.2. Ejemplo de uso de la negación y el corte
borra(L1,X,L2)se verifica siL2es la lista obtenida eliminando los elementos deL1unificables simultáneamente conX; por ejemplo,?- borra([a,b,a,c],a,L). L = [b, c] ; false. ?- borra([a,Y,a,c],a,L). Y = a L = [c] ; false. ?- borra([a,Y,a,c],X,L). Y = X, X = a, L = [c] ; false.
Definición con
not(borra.pl).borra_1([],_,[]). borra_1([X|L1],Y,L2) :- X=Y, borra_1(L1,Y,L2). borra_1([X|L1],Y,[X|L2]) :- not(X=Y), borra_1(L1,Y,L2).
Definición con corte (borra.pl).
borra_2([],_,[]). borra_2([X|L1],Y,L2) :- X=Y, !, borra_2(L1,Y,L2). borra_2([X|L1],Y,[X|L2]) :- % not(X=Y), borra_2(L1,Y,L2).
Definición con corte y simplificada (borra.pl).
borra_3([],_,[]). borra_3([X|L1],X,L2) :- !, borra_3(L1,X,L2). borra_3([X|L1],Y,[X|L2]) :- % not(X=Y), borra_3(L1,Y,L2).
3. El condicional
Definición de
notacon el condicional (notas_3.pl).nota(X,Y) :- X < 5 -> Y = suspenso ; % R1 X < 7 -> Y = aprobado ; % R2 X < 9 -> Y = notable ; % R3 true -> Y = sobresaliente. % R4
Definición del condicional y verdad:
P -> Q :- P, !, Q. % Def. -> 1 true. % Def. true
¿Cuál es la calificación correspondiente a un
6?:?- nota(6,X). X = aprobado.
- Árbol de deducción correspondiente a la pregunta
?- nota(6,Y).
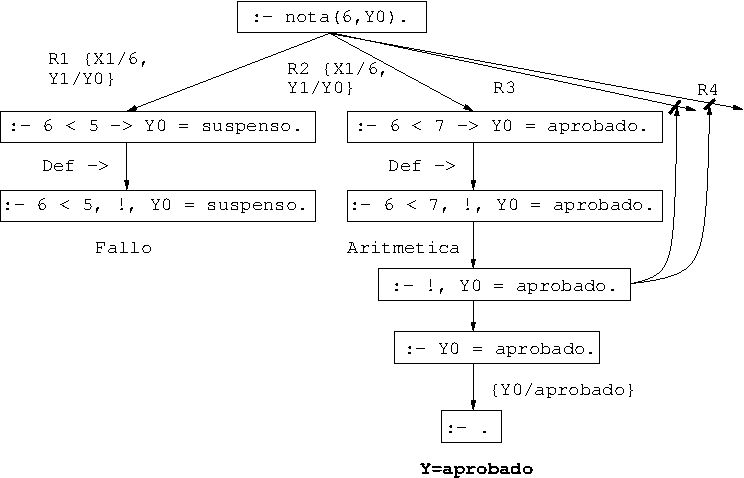
Ejemplo: ¿Es
6sobresaliente?:?- nota(6,sobresaliente). true.
4. Ejercicios
4.1. Diferencia de conjuntos
Ejercicio 1. Definir la relación diferencia(C1,C2,C3) que se verifica si C3 es
la diferencia de los conjuntos C1 y C2. Por ejemplo,
?- diferencia([a,b],[b,c],X). X = [a] ; false.
Escribir una versión con not y otra con corte.
1ª solución (con not)
diferencia_1([],_,[]). diferencia_1([X|C1],C2,C3) :- member(X,C2), diferencia_1(C1,C2,C3). diferencia_1([X|C1],C2,[X|C3]) :- not(member(X,C2)), diferencia_1(C1,C2,C3).
2ª solución (con corte)
diferencia_2([],_,[]). diferencia_2([X|C1],C2,C3) :- member(X,C2), !, diferencia_2(C1,C2,C3). diferencia_2([X|C1],C2,[X|C3]) :- % not(member(X,C2)), diferencia_2(C1,C2,C3).
4.2. Agregación de elementos a conjuntos
Ejercicio 2. Definir la relación agregar(X,L,L1) que se verifica si L1 es la
lista obtenida añadiéndole X a L, si X no pertenece a L y es L en caso
contrario. Por ejemplo,
?- agregar(a,[b,c],L). L = [a, b, c] ?- agregar(b,[b,c],L). L = [b, c]
1ª solución
agregar_1(X,L,[X|L]) :- not(member(X,L)). agregar_1(X,L,L) :- member(X,L).
2ª solución
agregar_2(X,L,L) :- memberchk(X,L), !. agregar_2(X,L,[X|L]).
4.3. Separación de positivos de no positivos
Ejercicio 3. Definir la relación separa(L1,L2,L3) que separa la lista de
números L1 en dos listas: L2 formada por los números positivos y L3 formada
por los números negativos o cero. Por ejemplo,
?- separa([2,0,-3,5,0,2],L2,L3). L2 = [2, 5, 2]. L3 = [0, -3, 0]
Escribir dos soluciones, una sin corte y otra con corte.
1ª solución (sin corte)
separa_1([],[],[]). separa_1([N|RL1],[N|RL2],L3) :- N > 0, separa_1(RL1,RL2,L3). separa_1([N|RL1],L2,[N|RL3]) :- N =< 0, separa_1(RL1,L2,RL3).
2ª solución (con corte)
separa_2([],[],[]). separa_2([N|RL1],[N|RL2],L3) :- N > 0, !, separa_2(RL1,RL2,L3). separa_2([N|RL1],L2,[N|RL3]) :- % N =< 0, separa_2(RL1,L2,RL3).
4.4. Suma de los números pares
Ejercicio 4. Definir la relación suma_pares(L,N) que se verifica si N es
la suma de todos los números pares de la lista L. Por ejemplo,
?- suma_pares([2,3,4],N). N = 6 ?- suma_pares([1,3,5,6,9,11,24],N). N = 30
Escribir una versión con negación y otra con corte.
1ª solución (con negación)
suma_pares_1([],0). suma_pares_1([N|L],X) :- par(N), suma_pares_1(L,X1), X is X1 + N. suma_pares_1([_N|L],X) :- not(par(_N)), suma_pares_1(L,X). par(N):- N mod 2 =:= 0.
2ª solución (con corte)
suma_pares_2([],0). suma_pares_2([N|L],X) :- par(N), !, suma_pares_2(L,X1), X is X1 + N. suma_pares_2([_N|L],X) :- % not(par(_N)), suma_pares_2(L,X).
3ª solución (con corte y acumulador)
suma_pares_3(L,X):- suma_pares_3_aux(L,0,X). suma_pares_3_aux([],Ac,Ac). suma_pares_3_aux([N|L],Ac,X) :- par(N), !, Ac1 is Ac + N, suma_pares_3_aux(L,Ac1,X). suma_pares_3_aux([_N|L],Ac,X) :- % not(par(_N)), suma_pares_3_aux(L,Ac,X).
Comparación de eficiencia
La comparación es
?- time((X is 10^6, numlist(1,X,L), suma_pares_1(L,N))). % 6,500,006 inferences, 2.682 CPU in 2.688 seconds (100% CPU, 2423324 Lips) X = 1000000, L = [1, 2, 3, 4, 5, 6, 7, 8, 9|...], N = 250000500000 ?- time((X is 10^6, numlist(1,X,L), suma_pares_2(L,N))). % 4,500,007 inferences, 2.111 CPU in 2.111 seconds (100% CPU, 2132088 Lips) X = 1000000, L = [1, 2, 3, 4, 5, 6, 7, 8, 9|...], N = 250000500000. ?- time((X is 10^6, numlist(1,X,L), suma_pares_3(L,N))). % 4,500,008 inferences, 0.417 CPU in 0.417 seconds (100% CPU, 10794334 Lips) X = 1000000, L = [1, 2, 3, 4, 5, 6, 7, 8, 9|...], N = 250000500000.
4.5. Exponente de 2 en la factorización prima
Ejercicio 5. Definir la relación exponente_de_dos(N,Exp) que se verifica si
E es el exponente de 2 en la descomposición de N como producto de factores
primos. Por ejemplo,
?- exponente_de_dos(40,E). E = 3 ?- exponente_de_dos(49,E). E = 0
Escribir una versión con negación y otra con corte.
1ª solución (con negación)
exponente_de_dos_1(N,E):- N mod 2 =:= 0, N1 is N / 2, exponente_de_dos_1(N1,E1), E is E1 + 1. exponente_de_dos_1(N,0) :- N mod 2 =\= 0.
2ª solución (con corte)
exponente_de_dos_2(N,E):- N mod 2 =:= 0, !, N1 is N / 2, exponente_de_dos_2(N1,E1), E is E1 + 1. exponente_de_dos_2(_,0).
4.6. Uso y variante de concatenación para calcular prefijo
Ejercicio 6. En los distintos apartados de este ejercicio se usará la relación
conc cuya definición se muestra a continuación.
conc([],L,L). conc([X|L1],L2,[X|L3]) :- conc(L1,L2,L3).
Ejercicio 6.1. Encontrar todas las listas L tal que al concatenar L con [c,d]
devuelva [a,b,c,d].
Solución
?- conc(L,[c,d],[a,b,c,d]). L = [a, b] ; false.
Ejercicio 6.2. Si obtener prefijos de esta forma fuera el único uso de conc
en nuestro programa, ¿podríamos modificar su definición para mejorar la
eficiencia?
conc_1([],L,L) :- !. conc_1([X|RL1],L2,[X|RL3]) :- conc_1(RL1,L2,RL3).
Ejemplo:
?- conc_1(L,[c,d],[a,b,c,d]). L = [a, b] ; false.
Ejercicio 6.3. ¿Serviría esa modificación para el uso general de conc?
No, por ejemplo
?- conc_1(L1,L2,[a,b,c]). L1 = [] L2 = [a, b, c]. ?- conc(L1,L2,[a,b,c]). L1 = [], L2 = [a, b, c] ; L1 = [a], L2 = [b, c] ; L1 = [a, b], L2 = [c] ; L1 = [a, b, c], L2 = [] ; false.
4.7. Signos de crecimientos de sucesiones numéricas
Ejercicio 7. Definir la relación crecimientos(+L1,-L2) que se
verifique si L2 es la lista correspondientes a los crecimientos de la
lista numérica L1; es decir, entre cada par de elementos consecutivos
X e Y de L1 coloca el signo + si X < Y e y signo - en caso
contrario. Por ejemplo,
?- crecimientos([1,3,2,2,5,3],L). L = [1, +, 3, -, 2, -, 2, +, 5, -]
1ª solución (sin corte)
crecimientos_1([_],[]). crecimientos_1([X,Y|L1],[X,+|L2]) :- X < Y, crecimientos_1([Y|L1],L2). crecimientos_1([X,Y|L1],[X,-|L2]) :- X >= Y, crecimientos_1([Y|L1],L2).
2ª solución (con corte)
crecimientos_2([_],[]). crecimientos_2([X,Y|L1],[X,+|L2]) :- X < Y, !, crecimientos_2([Y|L1],L2). crecimientos_2([X,Y|L1],[X,-|L2]) :- % X >= Y, crecimientos_2([Y|L1],L2).
4.8. Descomposición en factores primos
Ejercicio 8.1. Definir la relación menor_divisor_propio(+N,?X) que
se verifique si X es el menor divisor de N mayor o igual que 2. Por
ejemplo,
?- menor_divisor_propio(30,X). X = 2 ?- menor_divisor_propio(3,X). X = 3
Solución
menor_divisor_propio(N,X) :- N1 is floor(sqrt(N)), between(2,N1,X), N mod X =:= 0, !. menor_divisor_propio(N,N).
Ejercicio 8.2. Definir la relación factorización(+N,-L) que se
verifique si L es la lista correspondiente a la descomposición del
número N en factores primos (se considera los que elementos de L
están ordenados de manera creciente). Por ejemplo,
?- factorización(12,L). L = [2, 2, 3] ; false. ?- factorización(1,L). L = [] ; false.
Solución
factorización(1,[]). factorización(N,[X|L]) :- N > 1, menor_divisor_propio(N,X), N1 is N/X, factorización(N1,L).
4.9. Menor múltiplo con suma de sus dígitos mayor que N
Ejercicio 9. Definir la relación calcula(+N,+M,?X) que se verifique
si X es el menor múltiplo de N tal que la suma de sus dígitos es
mayor que M. Por ejemplo,
?- calcula(3,10,X). X = 39. ?- calcula(7,20,X). X = 399 .
Solución
calcula(N,M,X) :- múltiplo(N,X), suma_dígitos(X,N1), N1 > M, !.
múltiplo(+N,-X)se verifica siXes un múltiplo deN. Por ejemplo,?- múltiplo(5,X). X = 5 ; X = 10 ; X = 15.
Su definición es
múltiplo(N,N). múltiplo(N,M) :- múltiplo(N,N1), M is N+N1.
La relación
suma_dígitos(+N,-S)se verifica siSes la suma de los dígitos del númeroN. Por ejemplo,?- suma_dígitos(237,S). S = 12
Su definición es
suma_dígitos(N,N) :- N < 10, !. suma_dígitos(N,S) :- % N >= 10, N1 is N // 10, R is N - 10*N1, suma_dígitos(N1,S1), S is S1 + R.
2ª definición de
suma_dígitossuma_dígitos_2(N,S) :- dígitos(N,L), sum_list(L,S).
dígitos(N,L)se verifica siLes la lista de los dígitos deN. Por ejemplo.?- dígitos(325,L). L = [3,2,5].
Su definición es
dígitos(N,L) :- name(N,L1), maplist(plus(-48),L1,L).
4.10. Números libres de cuadrados
Ejercicio 10. Un número es libre de cuadrados si no es divisible por el cuadrado de ningún número mayor que 1.
Definir la relación libre_de_cuadrados(+N) que se verifique si el
número N es libre de cuadrados. Por ejemplo,
?- libre_de_cuadrados(30). true. ?- libre_de_cuadrados(12). false.
1ª solución
libre_de_cuadrados(N) :- M is floor(sqrt(N)), not((between(2,M,X), N mod (X*X) =:= 0)).
2ª solución
libre_de_cuadrados_2(N) :- M is floor(sqrt(N)), forall(between(2,M,X), N mod (X*X) =\= 0).
4.11. Suma de los números libres de cuadrados
Ejercicio 11. Definir la relación suma_libres_de_cuadrados(+L,-S)
que se verifique si S es la suma de los números libres de cuadrados la
lista numérica L. Por ejemplo,
?- suma_libres_de_cuadrados([6,12,18,30],S). S = 36 .
1ª solución (sin cortes)
suma_libres_de_cuadrados_1([],0). suma_libres_de_cuadrados_1([X|L],S) :- libre_de_cuadrados(X), suma_libres_de_cuadrados_1(L,S1), S is X+S1. suma_libres_de_cuadrados_1([X|L],S) :- not(libre_de_cuadrados(X)), suma_libres_de_cuadrados_1(L,S).
2ª solución (con cortes)
suma_libres_de_cuadrados_2([],0). suma_libres_de_cuadrados_2([X|L],S) :- libre_de_cuadrados(X), !, suma_libres_de_cuadrados_2(L,S1), S is X+S1. suma_libres_de_cuadrados_2([_X|L],S) :- % not(libre_de_cuadrados(_X)), suma_libres_de_cuadrados_2(L,S).
3ª solución
suma_libres_de_cuadrados_3(L,S) :- include(libre_de_cuadrados, L, L1), sum_list(L1,S).
4.12. Longitud de las subsucesiones comunes maximales
Ejercicio 12. Definir la relación longitud_scm(+L1,+L2,-N) que se
verifique si N es la longitud de las subsucesiones comunes maximales
de las listas L1 y L2. Por ejemplo,
?- longitud_scm([2,1,4,5,2,3,5,2,4,3],[1,7,5,3,2],N). N = 4 ; false.
ya que [1,5,3,2] es una subsucesión de las dos listas y no poseen
ninguna otra subsucesión común de mayor longitud. Obsérvese que los
elementos de la subsucesión no son necesariamente elementos adyacentes
en las listas.
Solución
longitud_scm([],_,0). longitud_scm(_,[],0). longitud_scm([X|L1],[X|L2],N) :- !, longitud_scm(L1,L2,M), N is M+1. longitud_scm([X|L1],[Y|L2],N) :- % X \= Y, longitud_scm(L1,[Y|L2],N1), longitud_scm([X|L1],L2,N2), N is max(N1,N2).
4.13. Elementos repetidos en una lista
Ejercicio 13.1. Definir la relación repetido(-A,+L) que se verifique
si el elemento A está repetido (i.e. ocurre más de una vez) en la
lista L. Por ejemplo,
?- repetido(A,[1,2,1,3,4,3]). A = 1 ; A = 1 ; A = 3 ; A = 3 ; false. ?- repetido(A,[1,2,5]). false.
3ª solución
repetido(A,L) :- select(A,L,R), memberchk(A,R).
Ejercicio 13.2. Definir la relación elimina(+X,+L1,-L2) que se
verifique si L2 es la lista obtenida eliminando todas las ocurrencias
de X en la lista L1. Por ejemplo,
?- elimina(a,[1,a,b,3,a,a,4,a,c],L). L = [1, b, 3, 4, c]
Solución
elimina(_,[],[]). elimina(X,[X|L1],L2) :- elimina(X,L1,L2). elimina(X,[Y|L1],[Y|L2]) :- X \= Y, elimina(X,L1,L2).
Ejercicio 13.3. Definir la relación repetidos(+L1,-L2) que se
verifique si L2 es la lista de los elementos repetidos de la lista
L1. Por ejemplo,
?- repetidos([1,2,4,3,4,1,3,5],L). L = [1, 4, 3]
1ª solución
repetidos_1([],[]). repetidos_1([X|L1],[X|L2]) :- memberchk(X,L1), elimina(X,L1,L3), repetidos_1(L3,L2). repetidos_1([X|L1],L2) :- not(memberchk(X,L1)), repetidos_1(L1,L2).
2ª solución
repetidos_2([],[]). repetidos_2([X|L1],[X|L2]) :- memberchk(X,L1), !, elimina(X,L1,L3), repetidos_2(L3,L2). repetidos_2([_X|L1],L2) :- % not(memberchk(_X,L1)), repetidos_2(L1,L2).
4.14. Subconjunto maximal
Ejercicio 14. Definir la relación subconjunto_maximal(+L1,-L2) que
se verifica si L2 es un subconjunto maximal de L1 (es decir, es un
conjunto de elementos de L1 tal que sólo existe un elemento de L1
que no pertenece a L2). Por ejemplo,
?- subconjunto_maximal([c,b,a,b,c,a,c],L). L = [b,a] ; L = [c,a] ; L = [c,b].
Solución
subconjunto_maximal(L1,L2) :- list_to_set(L1,L3), select(_,L3,L2).
4.15. Suma de los elementos con posiciones múltiplos de n
Ejercicio 15. Definir la relación suma_posiciones(+N,+L,-S) que se
verifique si S es la suma de los elementos de la lista que ocupan las
posiciones que son múltiplos de N. Por ejemplo,
?- suma_posiciones(2,[3,5,7,9,1,2],S). S = 16. ?- suma_posiciones(3,[3,5,7,9,1,2],S). S = 9.
Solución
suma_posiciones(N,L,S) :- elemento_y_resto(N,L,X,L1), !, suma_posiciones(N,L1,S1), S is X+S1. suma_posiciones(_,_,0).
elemento_y_resto(+N,+L1,-X,-L2)se verifica siXes el elementoN-ésimo deL1yL2es la listaL1a partir de dicho elemento. Por ejemplo,?- elemento_y_resto(3,[3,5,7,9,1,2],X,L). X = 7 L = [9, 1, 2].
Su definición es
elemento_y_resto(N,L1,X,L2) :- length(L,N), append(L,L2,L1), last(L,X).
4.16. Compresión de listas
Ejercicio 16. Definir la relación comprimida(+L1,-L2) que se
verifique si L2 es la lista obtenida sustituyendo cada sucesión de un
elemento de L1 por dicho elemento. Por ejemplo,
?- comprimida([a,b,b,a,a,a,c,c,b,b,b],L). L = [a, b, a, c, b]
1ª solución (sin corte)
comprimida([],[]). comprimida([X],[X]). comprimida([X,X|L1],L2) :- comprimida([X|L1],L2). comprimida([X,Y|L1],[X|L2]) :- X \= Y, comprimida([Y|L1],L2).
2ª solución (con corte)
comprimida_2([],[]). comprimida_2([X],[X]). comprimida_2([X,Y|L1],L2) :- X = Y, !, comprimida_2([X|L1],L2). comprimida_2([X,Y|L1],[X|L2]) :- % X \= Y, comprimida_2([Y|L1],L2).
4.17. Empaquetamiento de listas
Ejercicio 17. Definir la relación empaquetada(+L1,-L2) que se
verifique si L2 es la lista obtenida sustituyendo cada sucesión de un
elemento de L1 por la lista formada por dicha sucesión. Por ejemplo,
?- empaquetada([a,b,b,a,a,a,c,c,b,b,b],L). L = [[a], [b, b], [a, a, a], [c, c], [b, b, b]]
Solución
empaquetada([],[]). empaquetada([X|L1],[L2|L3]) :- empaquetada_aux(X,L1,L4,L2), empaquetada(L4,L3).
empaquetada_aux(X,L1,L4,L2)se verifica siL4es la lista obtenida eliminando enL1todas las ocurrencias iniciales deXyL2es la lista formada porXy las ocurrencias iniciales deXenL1; por ejemplo,?- empaquetada_aux(a,[a,a,c,c,b,b,b],L4,L2). L4 = [c, c, b, b, b] L2 = [a, a, a]
Su definición es
empaquetada_aux(X,[],[],[X]). empaquetada_aux(X,[X|L1],L4,[X|L2]) :- empaquetada_aux(X,L1,L4,L2). empaquetada_aux(X,[Y|L1],[Y|L1],[X]) :- X \= Y.
La definición anterior puede transformarse introduciendo corte en
empaquetada_aux_2(X,[],[],[X]). empaquetada_aux_2(X,[X|L1],L4,[X|L2]) :- !, empaquetada_aux_2(X,L1,L4,L2). empaquetada_aux_2(X,[Y|L1],[Y|L1],[X]).
4.18. Codificación por longitud
Ejercicio 18 Definir la relación codificada(+L1,-L2) que se
verifique si L2 es la codificación por longitud de la lista L1; es
decir, las sucesiones de un mismo elemento X de L1 se codifican por
términos de la forma N-X donde N es la longitud de la sucesión. Por
ejemplo,
?- codificada([a,b,b,a,a,a,c,c,b,b,b],L). L = [1-a, 2-b, 3-a, 2-c, 3-b]
1ª solución
codificada(L1,L2) :- empaquetada(L1,L), codificada_aux(L,L2).
codificada_aux(+L1,-L2)se verifica si, suponiendo queL1es una lista de la forma[[E1,...,E1],...,[Em,....Em]]),L2es la lista[N1-E1,...Nm-Em]dondeNies la longitud de[Ei,...,Ei]. Por ejemplo.?- codificada_aux([[a],[b,b],[a,a,a],[c,c],[b,b,b]],L). L = [1-a, 2-b, 3-a, 2-c, 3-b].
Su definición es
codificada_aux([],[]). codificada_aux([[X|Y]|L1],[N-X|L2]) :- length([X|Y],N), codificada_aux(L1,L2).
2ª solución
codificada_2(L1,L2) :- empaquetada(L1,L), codificada_aux_2(L,L2). codificada_aux_2(L1,L2) :- bagof(N-X, X^L3^(member([X|L3],L1), length([X|L3],N)), L2).
4.19. Codificación reducida por longitud
Ejercicio 19. Definir la relación codificada_reducida(+L1,-L2) que
se verifique si L2 es la codificación reducida por longitud de la
lista L1; es decir, las sucesiones de un mismo elemento X de L1 se
codifican por términos de la forma N-X donde N es la longitud de la
sucesión cuando N es mayor que 1 y por X cuando N es igual
a 1. Por ejemplo,
?- codificada_reducida([a,b,b,a,a,a,c,b,b,b],L). L = [a, 2-b, 3-a, c, 3-b]
1ª solución
codificada_reducida_1(L1,L2) :- codificada(L1,L), codificada_reducida_aux(L,L2).
codificada_reducida_aux(+L1,-L2)se verifica siL2es la lista obtenida transformando los elementos deL1de la forma1-XporXy dejando los restantes elementos de la misma forma (se supone queL1es una lista de la forma[N1-E1,...,Nm-Em]). Por ejemplo,?- codificada_reducida_aux([1-a,2-b,3-a,1-c,3-b],L). L = [a, 2-b, 3-a, c, 3-b]
Su definición es
codificada_reducida_aux([],[]). codificada_reducida_aux([1-X|L1],[X|L2]) :- codificada_reducida_aux(L1,L2). codificada_reducida_aux([N-X|L1],[N-X|L2]) :- N > 1, codificada_reducida_aux(L1,L2).
2ª solución
codificada_reducida_2(L1,L2) :- codificada(L1,L), codificada_reducida_aux_2(L,L2). codificada_reducida_aux_2([],[]). codificada_reducida_aux_2([1-X|L1],[X|L2]) :- !, codificada_reducida_aux_2(L1,L2). codificada_reducida_aux_2([N-X|L1],[N-X|L2]) :- % N > 1, codificada_reducida_aux_2(L1,L2).
4.20. Decodificación de lista
Ejercicio 20. Definir la relación decodificada(+L1,-L2) que, dada la
lista L1, devuelve la lista L2 cuya codificación reducida por
longitud es L1. Por ejemplo,
?- decodificada([a,2-b,3-a,c,3-b],L). L = [a, b, b, a, a, a, c, b, b, b]
Solución
decodificada([],[]). decodificada([1-X|L1],[X|L2]) :- !, decodificada(L1,L2). decodificada([N-X|L1],[X|L2]) :- % N > 1, !, N1 is N - 1, decodificada([N1-X|L1],L2). decodificada([X|L1],[X|L2]) :- % X es atómico decodificada(L1,L2).
4.21. Dientes de sierra
Ejercicio 21.1. Definir la relación diente(+L,-L1,-X,-L2) que se
verifique si L se compone de una lista L1 de números estrictamente
creciente hasta un cierto número X que llamaremos cima, de la cima y
de una lista L2 de números estrictamente decreciente. Las listas tiene
L1 y L2 tienen que ser no vacías y la cima X es el mayor elemento
de L. Por ejemplo,
?- diente([1,2,5,4,3,1],L1,X,L2). L1 = [1, 2] X = 5 L2 = [4, 3, 1] ; false. ?- diente([1,2,5],L1,X,L2). false.
Las listas que poseen esta forma de descomposición se llaman dientes.
Solución
diente(L,[X1|L1],X,[X2|L2]) :- append([X1|L1],[X,X2|L2],L), creciente([X1|L1]), last([X1|L1],Y), Y < X, decreciente([X,X2|L2]).
creciente(+L)se verifica si la lista de númerosLes estrictamente creciente.creciente([_]). creciente([A,B|L]) :- A < B, creciente([B|L]).
decreciente(+L)se verifica si la lista de númerosLes estrictamente decreciente.decreciente([_]). decreciente([A,B|L]) :- A > B, decreciente([B|L]).
Ejercicio 21.2. Una sierra es una lista numérica compuesta por la yuxtaposición de dientes. Nótese que dos dientes consecutivos deben compartir un elemento. Por ejemplo [1,2,1,3,1] es una sierra compuesta por los dientes [1,2,1] y [1,3,1], pero [1,2,1,1,3,1] no es una sierra.
Definir la relación dientes_de_sierra(+L1,?L2) que se verifique si
L1 es una sierra y L2 es la lista de los dientes de L1. Por
ejemplo,
?- dientes_de_sierra([1,2,1,3,1],L). L = [[1, 2, 1], [1, 3, 1]] ; false. ?- dientes_de_sierra([1,2,1,1,3,1],L). false.
Solución
dientes_de_sierra(L,[L]) :- diente(L,_,_,_), !. dientes_de_sierra(L,[L1|R]) :- append(L1,L2,L), diente(L1,_,_,_), last(L1,X), dientes_de_sierra([X|L2],R).
5. Bibliografía
- J.A. Alonso
Introducción a la programación lógica con Prolog.
- Cap. 7: "Control mediante corte"
- Cap. 8: "Negación
- I. Bratko
Prolog programming for artificial intelligence (3 ed.)
(Addison–Wesley, 2001)
- Cap. 5: "Controlling backtracking"
- W.F. Clocksin y C.S. Mellish
Programming in Prolog.
(Springer Verlag, 1994)
- Cap. 4: "Backtracking and the cut"
- T. Cornell.
Introduction to Prolog.
(Universität Tübingen, 1998).
- Cap. 11: Negation-as-failure and cut.
- U. Endriss.
An introduction to Prolog programming.
- Cap. 5: Backtracking, cuts and negation.
- W. Ertel. Introduction to artificial intelligence (2E). (Springer Verlag, 2017). Cap. 5.3: Execution control and procedural elements.
- T. Smith.
Artificial intelligence programming in Prolog.
(Univ. of Edinburgh, 2004).
- Cap. 6: Backtracking.
- J.M. Spivey
Introduction to logic programming through Prolog.
(Prentice-Hall International, 1996).
- Cap. 8: Negation as failure.
- L. Sterling y E. Shapiro
The art of Prolog (2nd Edition).
(The MIT Press, 1994)
- Cap. 11: "Cuts and negation"