Tema 7: Aplicaciones: Grafos, reinas y mapas
1. Grafos
1.1. Representación de los grafos
- Un grafo (no orientado y sin nodos aislados) se representa mediante la
definición del predicado
grafo(G,A)que se verifica siGes el nombre del grafo yAes la lista de arcos deG(cada uno representado mediante un términoX-Y). La representación del siguiente grafo
b / | \ / | \ a | c | / | / |/ des
grafo(ejemplo1,[a-b,b-c,b-d,c-d]).
El grafo de las conexiones entre ciudades andaluzas vecinas es
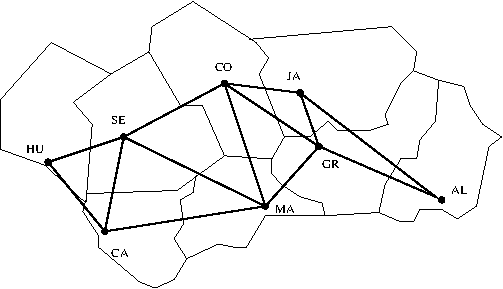 y su representación es
y su representación es
grafo(andalucía, [almería-granada, almería-jaén, cádiz-huelva, cádiz-málaga, cádiz-sevilla, córdoba-granada, córdoba-jaén, córdoba-málaga, córdoba-sevilla, granada-jaén, granada-málaga, huelva-sevilla, málaga-sevilla]).
arcos(G,L)se verifica siLes la lista de arcos del grafoG. Por ejemplo,?- arcos(ejemplo1,L). L = [a-b, b-c, b-d, c-d]. ?- arcos(andalucía,L). L = [almería-granada, almería-jaén, cádiz-huelva, cádiz-málaga, cádiz-sevilla, córdoba-granada, córdoba-jaén, córdoba-málaga, ... - ...|...].
Su definición es
arcos(G,A) :- grafo(G,A).
adyacente(G,X,Y)se verifica siXeYson adyacentes en el grafoG. Por ejemplo,?- adyacente(ejemplo1,d,X). X = b ; X = c. ?- adyacente(andalucía,almería,X). X = granada ; X = jaén ; false.
Su definición es
adyacente(X,Y) :- arcos(L), (member(X-Y,L) ; member(Y-X,L)).
nodos(G,L)se verifica siLes la lista de nodos de grafo G. Por ejemplo,?- nodos(ejemplo1,L). L = [a, b, c, d]. ?- nodos(andalucía,L). L = [almería, cádiz, córdoba, granada, huelva, jaén, málaga, sevilla].
Su definición es
nodos(G,L) :- setof(X,Y^adyacente(G,X,Y),L).
nodo(G,N)se verifica siNes un nodo deG. Por ejemplo,?- nodo(ejemplo1,N). N = a ; N = b ; N = c ; N = d. ?- nodo(andalucía,N). N = almería ; N = cádiz ; N = córdoba ; N = granada ; N = huelva ; N = jaén ; N = málaga ; N = sevilla.
Su definición es
nodo(G,N) :- nodos(G,L), member(N,L).
- Nota: El código de esta sección se encuentra en representacion_de_grafos.pl.
1.2. Caminos en grafos
camino(G,A,Z,C)se verifica siCes un camino en el grafoGdesde el nodoAalZ. Por ejemplo,?- camino(ejemplo1,a,d,C). C = [a, b, d] ; C = [a, b, c, d] ; false. ?- camino(andalucía,sevilla,granada,C). C = [sevilla, huelva, cádiz, málaga, córdoba, jaén, almería, granada] ; C = [sevilla, cádiz, málaga, córdoba, jaén, almería, granada] ?- findall(C,camino(andalucía,sevilla,granada,C),_L), length(_L,N). N = 16.
Su definición es
camino(G,A,Z,C) :- camino_aux(G,A,[Z],C). % camino_aux(+G,+A,+CP,-C) se verifica si C es una camino en G compuesto de un % camino desde A hasta el primer elemento del camino parcial CP (con nodos % distintos a los de CP) junto CP. camino_aux(_,A,[A|C1],[A|C1]). camino_aux(G,A,[Y|C1],C) :- adyacente(G,X,Y), not(member(X,[Y|C1])), camino_aux(G,A,[X,Y|C1],C).
1.3. Caminos hamiltonianos
hamiltoniano(G,H)se verifica siHes un camino hamiltoniano en el grafoG(es decir, es un camino enGque pasa por todos sus nodos). Por ejemplo,?- hamiltoniano(ejemplo1,H). H = [a, b, c, d] ; H = [d, c, b, a] ; H = [c, d, b, a] ; H = [a, b, d, c] ; false. ?- hamiltoniano(andalucía,H). H = [sevilla, huelva, cádiz, málaga, córdoba, jaén, almería, granada] ; H = [huelva, sevilla, cádiz, málaga, córdoba, jaén, almería, granada] ?- hamiltoniano(andalucía,_H), length(_H,N). N = 8
Su definición es
% 1ª definición hamiltoniano(G,H) :- camino(G,_,_,H), cubre(G,H). % cubre(+G,+H) se verifica si el camino H cubre el grafo G (es decir, todos los % nodos de G pertenecen a H). cubre(G,H) :- igual_medida(G,H). % igual_medida(+G,+H) se verifica si el número de nodos del camino H es igual al % número de nodos del grafo G. igual_medida(G,H) :- length(H,MH), nodos(G,N), length(N,MH).
2ª definición de
hammitonianohamiltoniano_2(C) :- nodos(L), length(L,N), length(C,N), camino(_,_,C).
Comparación de eficiencia
?- time(findall(_C,hamiltoniano(andalucía,_C),_L)). % 119,184 inferences, 0.019 CPU in 0.019 seconds (100% CPU, 6237168 Lips) true. ?- time(findall(_C,hamiltoniano_2(andalucía,_C),_L)). % 47,111 inferences, 0.009 CPU in 0.009 seconds (100% CPU, 5344800 Lips) true.
- Nota: El código con las definiciones de
caminoyhamiltonianose encuentra en camino.pl.
1.4. Generacion de grafos completos
completo(+N,-G)se verifica siGes el grafo completo de ordenN. Por ejemplo,?- completo(3,G). G = [1-2, 1-3, 2-3]. ?- completo(4,G). G = [1-2, 1-3, 1-4, 2-3, 2-4, 3-4].
Su definición es
completo(N,G) :- findall(X-Y,arco_completo(N,X,Y),G). arco_completo(N,X,Y) :- N1 is N-1, between(1,N1,X), X1 is X+1, between(X1,N,Y).
1.5. Generación de grafos aleatorios
aleatorio(+P,+N,-G)se verifica siGes un subgrafo del grafo completo de ordenNdonde cada arco se ha elegido con la probabilidadP(0 <=P<= 1). Por ejemplo,?- aleatorio(0,4,G). G = []. ?- aleatorio(1,4,G). G = [1-2, 1-3, 1-4, 2-3, 2-4, 3-4]. ?- aleatorio(0.1,4,G). G = [2-3]. ?- aleatorio(0.1,4,G). G = [1-3, 1-4]. ?- aleatorio(0.8,4,G). G = [1-2, 1-3, 1-4, 2-3, 2-4]. ?- aleatorio(0.8,4,G). G = [1-3, 1-4, 2-3, 2-4].
Su definición es
aleatorio(P,N,G) :- findall(X-Y,(arco_completo(N,X,Y),probabilidad(Z),Z=<P),G). % probabilidad(X) se verifica si X es un número probabilidad en el intervalo % [0,1]. Por ejemplo, % ?- probabilidad(X). % X = 0.08. % % ?- probabilidad(X). % X = 0.023. probabilidad(X) :- Y is random(1000), X is Y/1000.
2. El problema de las reinas
2.1. Enunciado del problema de las reinas
- El problema de las N reinas consiste en colocar N reinas en un tablero
rectangular de dimensiones N por N de forma que no se encuentren más
de una en la misma línea: horizontal, vertical o diagonal.

2.2. 1ª solución del problema de las N reinas.
reinas_1(+N,-S)se verifica siSes una solución del problema de lasNreinas. Por ejemplo,?- reinas_1(4,S). S = [1-3, 2-1, 3-4, 4-2] ; S = [1-2, 2-4, 3-1, 4-3] ; false. ?- reinas_1(8,S). S = [1-4, 2-2, 3-7, 4-3, 5-6, 6-8, 7-5, 8-1] ?- findall(S,reinas_1(8,S),_L), length(_L,N). N = 92.
Su definición es
reinas_1(N,S) :- tablero(N,S), solución(N,S). % tablero(N,L) se verifica si L es una lista de posiciones que % representan las coordenadas de N reinas en el tablero. Por ejemplo, % ?- tablero(4,L). % L = [1-_8750, 2-_8738, 3-_8726, 4-_8714]. tablero(N,L) :- findall(X-_Y,between(1,N,X),L). % solucion_1(+N,?L) se verifica si L es una lista de pares de números % que representan las coordenadas de una solución del problema de las N % reinas. Por ejemplo, solución(_,[]). solución(N,[X-Y|L]) :- solución(N,L), between(1,N,Y), no_ataca(X-Y,L). % no_ataca(X-Y,L) se verifica si la reina en la posición X-Y no ataca a % las reinas colocadas en las posiciones correspondientes a los % elementos de la lista L. no_ataca(_,[]). no_ataca(X-Y,[X1-Y1|L]) :- X =\= X1, Y =\= Y1, X-X1 =\= Y-Y1, X-X1 =\= Y1-Y, no_ataca(X-Y,L).
2.3. 2ª solución del problema de las N reinas
reinas_2(+N,-S)se verifica siLes una lista de N números, [x(1),…,x(N)], de forma que si las reinas se colocan en las casillas (1, x(1)),…,(N, x(N)), entonces no se atacan entre sí. Por ejemplo,?- reinas_2(4,S). S = [2, 4, 1, 3] ; S = [3, 1, 4, 2] ; false. ?- reinas_2(8,S). S = [1, 5, 8, 6, 3, 7, 2, 4] ?- findall(S,reinas_2(8,S),_L), length(_L,N). N = 92.
Su definición es
reinas_2(N,S) :- numlist(1,N,S1), permutation(S1,S), segura(S). % segura(L) se verifica si L es una lista de números [x(1),...,x(m)] % tal que las reinas colocadas en las posiciones % (a,x(1)), ..., (a+m,x(m)) no se atacan entre sí. Por ejemplo, % ?- segura([3,4]). % true. % ?- segura([2,4]). % false. segura([]). segura([X|L]) :- segura(L), no_ataca(X,L,1). % no_ataca(Y,L,D) se verifica si Y es un número, L es una lista de % números [y(1),...,y(m)] y D es un número tales que las reinas colocada % en la posición (X,Y) no ataca a las colocadas en las posiciones % (X+D,y(1)),..., (X+D+m,y(m)). no_ataca(_, [], _ ). no_ataca(Y, [Y1|L], D) :- Y1-Y =\= D, Y-Y1 =\= D, D1 is D+1 , no_ataca(Y, L, D1).
2.4. 3ª solución del problema de las N reinas
reinas_3(+N,-S)se verifica siLes una lista deNnúmeros, [x(1),…,x(N)], de forma que si las reinas se colocan en las casillas (1, x(1)),…,(N, x(N)), entonces no se atacan entre sí. Por ejemplo,?- reinas_3(4,S). S = [2, 4, 1, 3] ; S = [3, 1, 4, 2] ; false. ?- reinas_3(8,S). S = [1, 5, 8, 6, 3, 7, 2, 4] ?- findall(S,reinas_3(8,S),_L), length(_L,N). N = 92.
Su definición es
reinas_3(N,L) :- numlist(1,N,L1), A is -N+1, B is N-1, numlist(A,B,L2), M is 2*N, numlist(2,M,L3), reinas_3_aux(L,L1,L1,L2,L3). % reinas_3_aux(?L,+Dx,+Dy,+Du,+Dv) se verifica si L es una permutación % de los elementos de Dy de forma que si L es [y1,..., yn] y Dx es % [1,..., n], entonces y(j) - j (1 ≤ j ≤ n) son elementos distintos de % Du e y(j) + j (1 ≤ j ≤ n) son elementos distintos de Dv. reinas_3_aux([],[],_Dy,_Du,_Dv). reinas_3_aux([Y|Ys],[X|Dx1],Dy,Du,Dv) :- select(Y,Dy,Dy1), U is X-Y, select(U,Du,Du1), V is X+Y, select(V,Dv,Dv1), reinas_3_aux(Ys,Dx1,Dy1,Du1,Dv1).
2.5. Comparación de eficiencia
La comparación es para las 8 reinas es
?- time((findall(S,reinas_1(8,S),_L), length(_L,N))). % 203,186 inferences, 0.022 CPU in 0.022 seconds (100% CPU, 9263998 Lips) N = 92. ?- time((findall(S,reinas_2(8,S),_L), length(_L,N))). % 1,249,646 inferences, 0.086 CPU in 0.086 seconds (100% CPU, 14476330 Lips) N = 92. ?- time((findall(S,reinas_3(8,S),_L), length(_L,N))). % 120,599 inferences, 0.017 CPU in 0.017 seconds (100% CPU, 7170581 Lips) N = 92.
Comparación para distintos valores de N.
+-----+----------------------+---------------------+---------------------+ | N | reinas_1 | reinas_2 | reinas_3 | +-----+-------------+--------+---------------------+---------------------+ | | inferencias | seg. | inferencias | seg. | inferencias | seg. | +-----+-------------+--------+-------------+-------+-------------+-------+ | 4 | 401 | 0.00 | 543 | 0.00 | 546 | 0.00 | | 6 | 8,342 | 0.00 | 20,844 | 0.01 | 6,660 | 0.01 | | 8 | 195,628 | 0.15 | 1,422,318 | 0.91 | 120,614 | 0.09 | | 10 | 5,303,845 | 4.05 | 150,300,540 | 96.82 | 2,774,095 | 2.01 | | 12 | 182,574,715 | 147.22 | | | 83,067,721 | 64.93 | +-----+-------------+--------+-------------+-------+-------------+-------+
3. Coloreado de mapas
- Un mapa puede representarse mediante la relación
mapa(N,L)dondeNes el nombre del mapa yLes la lista de los pares formados por cada una de las regiones del mapa y la lista de sus regiones vecinas. Por ejemplo, los mapas siguientes
+----------+----------+ +----+-----+-----+----+ | a | b | | a | b | c | d | +----+-----+-----+----+ +----+-----+-----+----+ | | | | | e | | f | | c | d | e | +----+ k +----+ | | | | | g | | h | +----+-----+-----+----+ +----+-----+-----+----+ | f | g | | i | j | +----------+----------+ +----------+----------+
se pueden representar por
mapa(ejemplo_1, [a-[b,c,d], b-[a,d,e], c-[a,d,f], d-[a,b,c,e,f,g], e-[b,d,g], f-[c,d,g], g-[d,e,f]]). mapa(ejemplo_2, [a-[b,e,k], b-[a,c,e,k], c-[b,d,f,k], d-[c,f,k], e-[a,b,g,k], f-[c,d,h,k], g-[e,i,k], h-[f,j,k], i-[g,j,k], j-[i,h,k], k-[a,b,c,d,e,f,g,h,i,j]]).
coloración(+M,+LC,-S)se verifica siSes una lista de pares formados por una región del mapaMy uno de los colores de la lista de coloresLCtal que las regiones vecinas tengan colores distintos. Por ejemplo,?- coloración(ejemplo_1,[1,2,3],S). S = [a-1, b-2, c-2, d-3, e-1, f-1, g-2]
Sus definiciones son
% 1ª solución % =========== coloración_1(M,LC,S) :- mapa(M,L), coloración_1_aux(L,LC,S). coloración_1_aux([],_,[]). coloración_1_aux([R-V|L],LC,[R-C|S]) :- member(C,LC), coloración_1_aux(L,LC,S), not((member(R1,V), member(R1-C,S))). % 2ª solución % =========== coloración_2(M,LC,S) :- mapa(M,L), coloración_2_aux(L,LC,[],S). coloración_2_aux([],_,S,S). coloración_2_aux([R-V|L],LC,A,S) :- member(C,LC), not((member(R1,V), member(R1-C,A))), coloración_2_aux(L,LC,[R-C|A],S).
La comparación es
?- set_prolog_flag(answer_write_options, [quoted(true), portray(true), max_depth(100)]). true. ?- time(coloración_1(ejemplo_2,[1,2,3,4],S)). % 18,002,577 inferences, 1.297 CPU in 1.297 seconds (100% CPU, 13875597 Lips) S = [a-1,b-2,c-1,d-2,e-3,f-3,g-1,h-1,i-2,j-3,k-4] ?- time(coloración_2(ejemplo_2,[1,2,3,4],S)). % 590 inferences, 0.000 CPU in 0.000 seconds (98% CPU, 1804977 Lips) S = [k-4,j-3,i-2,h-1,g-1,f-3,e-3,d-2,c-1,b-2,a-1]
Para determinar el número de colores necesarios para colorear el segundo mapa, se hacen los siguientes cálculos
?- findall(_S,coloración_2(ejemplo_2,[1,2,3],_S),_L), length(_L,N). N = 0. ?- findall(_S,coloración_2(ejemplo_2,[1,2,3,4],_S),_L), length(_L,N). N = 1032.
Por tanto, se necesitan 4 colores para colorear el segundo mapa y puede colorearse de 1032 formas con dicho número.
4. Ejercicios
Nota. Usaremos las relaciones de
camino.pl.:- [camino].
Nota: También usaremos los siguientes ejemplos de grafo
grafo(g1,[a-b,b-c,b-d,c-d]). grafo(g2,[a-b,c-d]). grafo(g3,[a-b,b-c,b-d]). grafo(g4,[a-b,b-c]).
4.1. Grafo conectado
Ejercicio 1. Definir la relación conectado(+G) que se verifica si el
grafo G está conectado; es decir, existe un camino entre cada par de
vértices distintos. Por ejemplo,
?- conectado(g1). true. ?- conectado(g2). false. ?- conectado(g3). true.
Solución
conectado(G) :- not((nodo(G,X), nodo(G,Y), not(camino(G,X,Y,_)))).
4.2. Grafo con ciclos
Ejercicio 2. Definir la relación tiene_ciclos(+G) que se verifica si
en el grafo G hay ciclos. Por ejemplo,
?- tiene_ciclos(g1). true ?- tiene_ciclos(g2). false. ?- tiene_ciclos(g3). false.
Solución
tiene_ciclos(G) :- adyacente(G,X,Y), camino(G,X,Y,[X,_,_|_]).
4.3. Árboles
Ejercicio 3. Definir la relación es_árbol(+G) que se verifica si G
es un árbol; es decir, G es un grafo conectado sin ciclos. Por
ejemplo,
?- es_árbol(g1). false. ?- es_árbol(g2). false. ?- es_árbol(g3). true.
Solución
es_árbol(G) :- conectado(G), not(tiene_ciclos(G)).
4.4. Grafo recubridor
Ejercicio 4. Definir la relación recubre(+G1,+G2) que se verifica si
el grafo G1 recubre el grafo G2 (es decir, todos los nodos del grafo
G2 son nodos del grafo G1). Por ejemplo,
?- recubre(g3,g4). true. ?- recubre(g4,g3). false.
Solución
recubre(G1,G2) :- not((nodo(G2,X), not(nodo(G1,X)))).
Ejercicio 4. Definir la relación árbol_de_expansión(+G,?A) que se
verifica si A es un árbol de expansión de G; es decir, A es un
subgrafo de G que es un árbol y recubre a G. Por ejemplo,
?- árbol_de_expansión(g1,A). A = grafo(ae2, [a-b, b-c, b-d]) ; A = grafo(ae3, [a-b, b-c, c-d]) ; A = grafo(ae5, [a-b, b-d, c-d]) ; false.
Solución
:- dynamic grafo/2. árbol_de_expansión(G,A) :- reset_gensym(ae), árbol_de_expansión_aux(G,A). árbol_de_expansión_aux(G,A) :- arcos(G,L1), subconjunto(L2,L1), gensym(ae,E), A =.. [grafo,E,L2], asserta(A), es_árbol(E), recubre(E,G). % subconjunto(?L1,+L2) se verifica si L1 es un subconjunto de L2. Por % ejemplo, % ?- subconjunto(L,[a,b,c]). % L = [a, b, c] ; % L = [a, b] ; % L = [a, c] ; % L = [a] ; % L = [b, c] ; % L = [b] ; % L = [c] ; % L = []. subconjunto([],[]). subconjunto([X|L1],[X|L2]) :- subconjunto(L1,L2). subconjunto(L1,[_|L2]) :- subconjunto(L1,L2).
4.5. Formación de grupos minimales de asignaturas compatibles
Ejercicio 5.1. Mediante la relación lista_de_clase(C,A,L) se
representa la información de los alumnos según los cursos y
asignaturas, de forma que C es el curso, A es la asignatura y L es
la lista de los alumnos de dicha asignatura. A lo largo del ejercicio
vamos a usar como ejemplo la siguiente información.
lista_de_clase(c1,asig1,[a1,a5]). lista_de_clase(c1,asig2,[a1,a2,a3]). lista_de_clase(c1,asig3,[a1,a3]). lista_de_clase(c1,asig4,[a2,a4,a6,a8]). lista_de_clase(c1,asig5,[a2,a4,a5]). lista_de_clase(c1,asig6,[a6,a7]). lista_de_clase(c1,asig7,[a3,a7]). lista_de_clase(c1,asig8,[a6,a7,a8]). lista_de_clase(c2,asig9,[a9,a11]). lista_de_clase(c2,asig10,[a10,a12]). lista_de_clase(c2,asig11,[a10,a11]). lista_de_clase(c2,asig12,[a9,a12]).
Definir la relación asignaturas(+C,-L) que se verifique si L es la
lista de asignaturas del curso C. Por ejemplo,
?- asignaturas(c1,L). L = [asig1,asig2,asig3,asig4,asig5,asig6,asig7,asig8]. ?- asignaturas(c2,L). L = [asig9,asig10,asig11,asig12].
Solución
asignaturas(C,L):- findall(X,lista_de_clase(C,X,_),L).
Ejercicio 5.2. Definir la relación grupo_incompatible(+L) que se
verifique si la lista de asignaturas L es incompatible (es decir,
algún alumno está en las listas de clase de más de una asignatura de
la lista L). Por ejemplo,
?- grupo_incompatible([asig1,asig2]). true ?- grupo_incompatible([asig1,asig4,asig7]). false.
Solución
grupo_incompatible(L):- select(X,L,R), member(Y,R), lista_de_clase(_,X,LX), lista_de_clase(_,Y,LY), member(A,LX), member(A,LY).
Ejercicio 5.3. Definir la relación lista_incompatible(+L) que
verifique si la lista de grupos de asignaturas L es incompatible (es
decir, contiene algún grupo incompatible de asignaturas). Por ejemplo,
?- lista_incompatible([[asig9, asig12], [asig11, asig10]]). true ?- lista_incompatible([[asig11, asig12], [asig9, asig10]]). false.
Solución
lista_incompatible(P) :- member(G,P), grupo_incompatible(G).
Ejercicio 5.4. Definir la relación extensión(+L1,+X,-L2) que se
verifique si L2 es la lista obtenida añadiendo X como primer elemento
de un elemento de L1 o L2 es la lista obtenida añadiendo [X] a
L1. Por ejemplo,
?- extensión([[a], [b, c]],d,E). E = [[d,a],[b,c]] ; E = [[a],[d,b,c]] ; E = [[a],[b,c],[d]].
Solución
extensión([],X,[[X]]). extensión([L|L1],X,[[X|L]|L1]). extensión([L|L1],X,[L|L2]) :- extensión(L1,X,L2).
Ejercicio 5.5. Definir la relación partición(+L,-P) que se verifique
si P es una partición de la lista L (es decir, un conjunto obtenido
distribuyendo los elementos de L en conjuntos no vacíos y sin
elementos comunes). Por ejemplo,
?- partición([a,b,c],P). P = [[a,b,c]] ; P = [[b,c],[a]] ; P = [[a,c],[b]] ; P = [[c],[a,b]] ; P = [[c],[b],[a]].
Solución
partición([],[]). partición([X|L1],L2) :- partición(L1,L3), extensión(L3,X,L2).
Ejercicio 5.6. Definir la relación agrupación_compatible_de_asignaturas(+C,-P)
que se verifique si P es una partición compatible de las asignaturas
del curso C. Por ejemplo,
?- agrupación_compatible_de_asignaturas(c2,P). P = [[asig11,asig12],[asig9,asig10]] ; P = [[asig11,asig12],[asig10],[asig9]] ; P = [[asig12],[asig11],[asig9,asig10]]
Solución
agrupación_compatible_de_asignaturas(C,P) :- asignaturas(C,L), partición(L,P), not(lista_incompatible(P)).
Ejercicio 5.7. Definir la relación agrupación_compatible_minimal(+C,-P)
que se verifique si P es una partición compatible de las asignaturas
del curso C con el menor número posible de grupos de asignaturas. Por
ejemplo,
?- agrupación_compatible_minimal(c2,P). P = [[asig11,asig12],[asig9,asig10]] ; false.
Solución
agrupación_compatible_minimal(C,P) :- agrupación_compatible_de_asignaturas(C,P), length(P,N), not((agrupación_compatible_de_asignaturas(C,P1),length(P1,M),M < N)).
Ejercicio 5.8. Calcular las agrupaciones compatibles minimales del
curso c1.
Solución
?- agrupación_compatible_minimal(c1,P). P = [[asig3,asig5,asig8],[asig1,asig4,asig7],[asig2,asig6]] ; P = [[asig2,asig8],[asig1,asig4,asig7],[asig3,asig5,asig6]] ; false.
4.6. Simulación de una calculadora básica
Ejercicio 6.1. El objetivo de los siguientes ejercicios es la simulación de una calculadora básica. Para ello consideraremos que en cada momento la calculadora se encuentra en un determinado estado caracterizado por una lista con cuatro elementos [UCE,UTA,UOA,VIM] donde
- UCE es el último cálculo efectuado,
- UTA es la última tecla activada,
- UOA es el último operador activado y
- VIM es el valor impreso.
El estado inicial es [0,=,=,0] y está definido por
estado_inicial([0,=,=,0]).
Las acciones posibles son pulsar un dígito, una operación aritmética o la de resultado y están definidas por
acción(X) :- es_dígito(X). acción(X) :- es_operación(X). acción(X) :- es_resultado(X). es_dígito(0). es_dígito(1). es_dígito(2). es_dígito(3). es_dígito(4). es_dígito(5). es_dígito(6). es_dígito(7). es_dígito(8). es_dígito(9). es_operación(+). es_operación(-). es_operación(*). es_operación(/). es_resultado(=).
En la siguiente tabla se muestran los estados de la calculadora correspondientes a las acciones indicadas en la última columna
| estado | tecla |
|---|---|
| ( 0, =, =, 0) | 3 |
| ( 0, 3, =, 3) | + |
| ( 3, +, +, 3) | 2 |
| ( 3, 2, +, 2) | 1 |
| ( 3, 1, +, 21) | * |
| (24, *, *, 24) | 2 |
| (24, 2, *, 2) | = |
| (48, =, =, 48) |
Es decir, si se parte del estado inicial y se realizan las acciones
3 + 2 1 * 2 =
se obtiene como resultado el número 48.
Definir la relación transición(+E1,+X,?E2)4 que se verifique si ~E2 es
el estado obtenido aplicando la acción X al estado E1; es decir, si E1
es [UCE,UTA,UOA,VIM], entonces
- Si
Xes un dígito, entonces- si
UTAes un dígito,E2es[UCE,X,UOA,10*VIM+X]; - en otro caso,
E24 es ~[UCE,X,UOA,X].
- si
- Si
Xno es un dígito, entonces- si
UOAes una operación,E2es[UOA(UCE,VIM),X,X,UOA(UCE,VIM)] - en otro caso,
E24 es ~[VIM,X,X,VIM].
- si
Por ejemplo,
?- estado_inicial(E1), transición(E1,3,E2), transición(E2,+,E3), transición(E3,2,E4), transición(E4,1,E5), transición(E5,*,E6), transición(E6,2,E7), transición(E7,=,E8). E1 = [0, =, =, 0] E2 = [0, 3, =, 3] E3 = [3, +, +, 3] E4 = [3, 2, +, 2] E5 = [3, 1, +, 21] E6 = [24, *, *, 24] E7 = [24, 2, *, 2] E8 = [48, =, =, 48].
1ª solución
transición_1([UCE,UTA,UOA,VIM],X,E) :- ( es_dígito(X) -> ( es_dígito(UTA) -> Y is 10*VIM+X, E = [UCE,X,UOA,Y] ; % \+ es_dígito(UTA) -> E = [UCE,X,UOA,X] ) ; % \+ es_dígito(X) -> ( es_operación(UOA) -> T =.. [UOA,UCE,VIM], Y is T, E = [Y,X,X,Y] ; % \+ es_operación(UOA) -> E = [VIM,X,X,VIM] )).
2ª solución
transición_2([UCE,UTA,UOA,VIM],X,E) :- ( es_dígito(X), es_dígito(UTA) -> Y is 10*VIM+X, E = [UCE,X,UOA,Y] ; es_dígito(X), \+ es_dígito(UTA) -> E = [UCE,X,UOA,X] ; \+ es_dígito(X), es_operación(UOA) -> T =.. [UOA,UCE,VIM], Y is T, E = [Y,X,X,Y] ; \+ es_dígito(X), es_resultado(UOA) -> E = [VIM,X,X,VIM] ).
3ª solución
transición_3([UCE,UTA,UOA,VIM],X,[UCE,X,UOA,Y]) :- es_dígito(X), es_dígito(UTA), Y is 10*VIM+X. transición_3([UCE,UTA,UOA,_VIM],X,[UCE,X,UOA,X]) :- es_dígito(X), \+ es_dígito(UTA). transición_3([UCE,_UTA,UOA,VIM],X,[Y,X,X,Y]) :- \+ es_dígito(X), es_operación(UOA), T =.. [UOA,UCE,VIM], Y is T. transición_3([_UCE,_UTA,=,VIM],X,[VIM,X,X,VIM]) :- \+ es_dígito(X).
En lo que sige usaremos la primera.
transición(E1,A,E2) :- transición_1(E1,A,E2).
Ejercicio 6.2. Definir la relación transiciones(+E1,+L,?E2) que se
verifique si E2 es el estado obtenido aplicando las acciones de la
lista L al estado E1. Por ejemplo,
?- estado_inicial(_E1), transiciones(_E1,[3,+,2,1,*,2,=],E2). E2 = [48, =, =, 48]
Solución
transiciones(E,[],E). transiciones(E1,[X|L],E3) :- transición(E1,X,E2), transiciones(E2,L,E3).
Ejercicio 6.3. Definir la relación acciones(?L) que se verifique si
L es una lista cuyos elementos son acciones. Por ejemplo,
?- acciones([2,+,3,7]). true ?- acciones([2,+,37]). false.
Solución
acciones([]). acciones([X|L]) :- acción(X), acciones(L).
Ejercicio 6.4. Calcular el número de posibles listas de acciones de longitud 3.
Solución
?- findall(_L,(length(_L,3), acciones(_L)),_LAL3), length(_LAL3,N). N = 3375.
Ejercicio 6.5. Definir la relación empieza_por_dígito(?L) que se
verifique si el primer elemento de la lista L es un dígito.
Solución
empieza_por_dígito([X|_L]) :- es_dígito(X).
Ejercicio 6.6. Definir la relación tiene_operaciones_consecutivas(?L)
que se verifique si la lista L contiene dos operaciones consecutivas.
Solución
tiene_operaciones_consecutivas(L) :- append(_A,[X,Y|_B],L), es_operación(X), es_operación(Y).
Ejercicio 6.7. Definir la relación tiene_resultado_intermedio(?L)
que se verifique si la lista L contiene el símbolo = en una posición
que no es la última.
Solución
tiene_resultado_intermedio(L) :- append(_A,[=,_Y|_B],L).
Ejercicio 6.8. Definir la relación divide_por_cero(?L) que se
verifique si en la lista L aparecen de manera consecutiva el símbolo
/ y un cero.
Solución
divide_por_cero(L) :- append(_A,[/,0|_B],L).
Ejercicio 6.9. Definir la relación termina_en_dígito_y_resultado(?L)
que se verifique si en la lista L los últimos elementos son un dígito
y el símbolo =.
Solución
termina_en_dígito_y_resultado(L) :- reverse(L,[=,X|_]), es_dígito(X).
Ejercicio 6.10. Definir la relación acciones_válidas(L) que se
verifique si L es una lista de acciones válidas.
Solución
acciones_válidas(L) :- acciones(L), empieza_por_dígito(L), not(tiene_operaciones_consecutivas(L)), not(tiene_resultado_intermedio(L)), not(divide_por_cero(L)), termina_en_dígito_y_resultado(L).
Ejercicio 6.11. Calcular el número de posibles listas de acciones válidas de longitud 3.
Solución
?- findall(_L,(length(_L,3), acciones_válidas(_L)),_LAL3), length(_LAL3,N). N = 100.
Ejercicio 6.12. Definir la relación cálculo(+N,+M,-L) que se
verifique si L es una lista de M acciones válidas que aplicadas al
estado inicial da como resultado el número N. Por ejemplo,
?- cálculo(5,2,L). L = [5,=] ; false. ?- cálculo(5,3,L). L = [0,5,=] ; false. ?- cálculo(5,4,L). L = [0,0,5,=] ; L = [0,+,5,=] ; L = [1,+,4,=] ; L = [1,*,5,=] ; L = [2,+,3,=] ; L = [3,+,2,=] ; L = [4,+,1,=] ; L = [5,+,0,=] ; L = [5,-,0,=] ; L = [5,*,1,=] ; L = [5,/,1,=] ; L = [6,-,1,=] ; L = [7,-,2,=]
Solución
cálculo(N,M,L) :- estado_inicial(E1), length(L,M), acciones_válidas(L), transiciones(E1,L,[N,=,=,N]).
4.7. Problema de las subastas
Ejercicio 7. En una subasta se hacen distintas ofertas. Cada oferta
incluye un lote de productos y un precio por dicho lote. Las ofertas
realizadas se representan mediante la relación oferta(O,L,P) que se
verifica si O es una oferta por el lote L con un coste P. Por
ejemplo, oferta(a,[1,2,3],30) representa la oferta a en la que se
puja por el lote compuesto por los objetos 1, 2 y 3 por un valor de 30
euros.
Para la aceptación de las ofertas se observan las siguientes reglas:
- No puede aceptar dos ofertas que contienen un mismo objeto en sus lotes.
- Se prefieren las ofertas de mayor ganancia.
Definir la relación aceptada(-L) que se verifique si L es una lista
de ofertas aceptadas. Por ejemplo, si las ofertas realizadas se definen
por
oferta(a,[1,2,3],30). oferta(b,[1,2,3],20). oferta(c,[4],20). oferta(d,[2,4],20). oferta(e,[1,2],20).
entonces,
?- aceptada(L). L = [a, c]
Solución
aceptada(L) :- aceptable(L), ganancia(L,G), not((aceptable(L1), ganancia(L1,G1), G1 > G)).
aceptable(?L)se verifica siLes una lista de ofertas aceptable; es decir, una lista de ofertas que no contienen objetos comunes en sus lotes. Por ejemplo, con la definición anterior deofertas/3,?- aceptable(L). L = [a, c] ; L = [a] ; L = [b, c] ; L = [b] ; L = [c, e] ; L = [c] ; L = [d] ; L = [e] ; L = [].
Su definición es
aceptable(L) :- lista_de_ofertas(L1), subconjunto(L,L1), es_aceptable(L).
lista_de_ofertas(-L)se verifica siL4 es la lista de todas las ofertas. Por ejemplo, con la definición anterior de ~ofertas/3,?- lista_de_ofertas(L). L = [a, b, c, d, e].
Su definición es
lista_de_ofertas(L) :- findall(O,oferta(O,_,_),L).
es_aceptable(+L)se verifica si la lista de ofertasLes aceptable; es decir, no contiene ofertas con objetos comunes en sus lotes. Por ejemplo, con la definición anterior deofertas/3,?- es_aceptable([c,e]). true. ?- es_aceptable([c,d]). false.
Su definición es
es_aceptable(L) :- not(es_inaceptable(L)).
es_inaceptable(+L)se verifica siLes una lista de ofertas inaceptable; es decir, contiene ofertas con objetos comunes en sus lotes. Por ejemplo, con la definición anterior deofertas/3,?- es_inaceptable([c,d]). true ?- es_inaceptable([c,e]). false.
Su definición es
es_inaceptable(L) :- member(O1,L), member(O2,L), O1 \= O2, oferta(O1,L1,_), oferta(O2,L2,_), se_solapan(L1,L2).
se_solapan(+L1,+L2)se verifica siL1yL2se solapan; es decir, tienen elementos comunes. Por ejemplo,?- se_solapan([a,b,c],[d,b,e]). true ?- se_solapan([a,b,c],[d,e]). false.
Su definición es
se_solapan(L1,L2) :- member(X,L1), member(X,L2).
ganancia(+L,-G)se verifica si la ganancia de la lista de ofertasLesG. Por ejemplo, con la definición anterior deofertas/3,?- ganancia([a,c],G). G = 50.
Su definición es
ganancia([],0). ganancia([O|L],G) :- oferta(O,_,G1), ganancia(L,G2), G is G1+G2.
5. Bibliografía
- I. Bratko.
Prolog programming for artificial intelligence (3 ed.)
(Addison-Wesley, 1990)
- Cap. 4: "Using structures: example programs"
- Cap. 9: "Operations on data structures"
- T. Cornell.
Introduction to Prolog.
(Universität Tübingen, 1998).
- Cap. 7: Graphs.
- J.M. Spivey
Introduction to logic programming through Prolog.
(Prentice-Hall International, 1996).
- Cap. 9: Searching problemas.
- L. Sterling y E. Shapiro.
The art of Prolog (2nd Edition).
(The MIT Press, 1994)
- Cap. 2 "Database programming"