| Inicial | Temas | Manuales | Ejercicios | Exámenes | Documentación

Tema 8: Resolución de problemas de espacios de estados

Índice

1. Ejemplo de problema mediante espacios de estados: el 8 puzzle

  • Para el 8 puzzle se usa un cajón cuadrado en el que hay situados 8 bloques cuadrados. El cuadrado restante está sin rellenar. Cada bloque tiene un número. Un bloque adyacente al hueco puede deslizarse hacia él. El juego consiste en transformar la posición inicial en la posición final mediante el deslizamiento de los bloques. En particular, consideramos el estado inicial y final siguientes:
    tema-8-8-puzzle-4.png
  • Ejemplos de movimientos
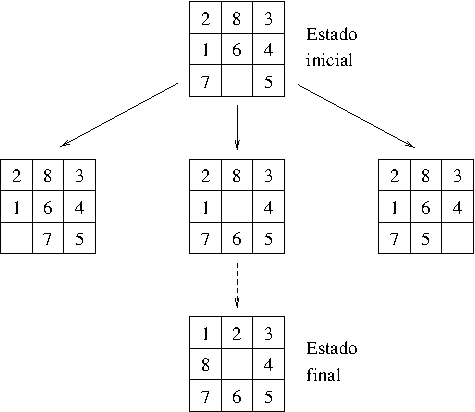
    tema-8-8-puzzle-1.png
  • Solución del 8–puzzle:
    tema-8-8-puzzle-3.png
  • Representación:
    • Estado inicial: [[2,8,3],[1,6,4],[7,h,5]]
    • Estado final: [[1,2,3],[8,h,4],[7,6,5]]
    • Operadores:
      • Mover el hueco a la izquierda
      • Mover el hueco arriba
      • Mover el hueco a la derecha
      • Mover el hueco abajo
  • Número de estados = 9! = 362.880.
  • Nota: El estudio del problema continúa en la última sección.

2. Búsqueda en profundidad sin ciclos

2.1. El problema del árbol

2.1.1. Descripción del problema del árbol

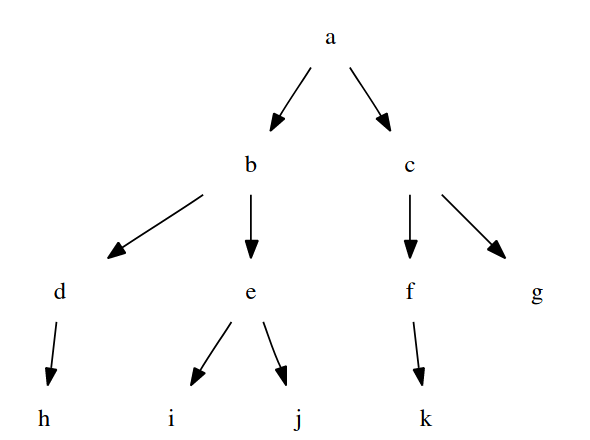
  • El problema del árbol consiste en encontrar caminos (desde a hasta f o j) en el siguiente grafo
    tema-8-arbol.png

2.1.2. Representación del problema del árbol

  • El problema se representa mediante las relaciones estado_inicial/1, estado_final/1 y sucesor/2 definidas a continuación.

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial(a).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(f).
estado_final(j).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(a,b).
sucesor(a,c).
sucesor(b,d).
sucesor(b,e).
sucesor(c,f).
sucesor(c,g).
sucesor(d,h).
sucesor(e,i).
sucesor(e,j).
sucesor(f,k).
  • El código del problema del árbol se encuentra en p_arbol.pl.

2.2. Procedimiento de búsqueda en profundidad sin ciclos

  • profundidad_sin_ciclos(?S) se verifica si S es una solución del problema mediante búsqueda en profundidad sin ciclos. Por ejemplo, Su definición es 

    profundidad_sin_ciclos(S) :-
   estado_inicial(E),
   profundidad_sin_ciclos(E,S).

  • profundidad_sin_ciclos(+E,?S) se verifica si S es una solución por búsqueda en profundidad sin ciclos a partir de E; es decir, según el siguiente procedimiento:

    • 1. S = [E] es una solución si E es un estado final.
    • 2. S = [E|S1] es una solución si existe un E tal que
      • 2.1. E1 es un sucesor de E
      • 2.2. S1 es una solución por búsqueda en profundidad sin ciclos a partir de E1.
    profundidad_sin_ciclos(E,[E]) :-
   estado_final(E).                 % 1
profundidad_sin_ciclos(E,[E|S1]) :- % 2
   sucesor(E,E1),                   % 2.1
   profundidad_sin_ciclos(E1,S1).   % 2.2
  • El código de la búsqueda en profundidad sin ciclos se encuentra en

2.3. Solución del problema del árbol mediante búsqueda en profundidad sin ciclos

  • La solución es 

    ?- [p_arbol, b_profundidad_sin_ciclos].
true

?- profundidad_sin_ciclos(S).
S = [a, b, e, j]

?- trace(estado_final,+call).
     estado_final/1: [call]
true.

?- profundidad_sin_ciclos(S).
 T Call: estado_final(a)
 T Call: estado_final(b)
 T Call: estado_final(d)
 T Call: estado_final(h)
 T Call: estado_final(e)
 T Call: estado_final(i)
 T Call: estado_final(j)
S = [a, b, e, j]

?- trace(estado_final,-call).
%         estado_final/1: Not tracing
true.

2.4. El problema de las 4 reinas

2.4.1. Descripción del problema de las 4 reinas

  • El problema de las 4 reinas consiste en colocar 4 reinas en un tablero rectangular de dimensiones 4 por 4 de forma que no se encuentren más de una en la misma línea: horizontal, vertical o diagonal.
  • Los estados son listas de números que representan las ordenadas de las reinas colocadas. Por ejemplo, [3,1] representa que se ha colocado las reinas (1,1) y (2,3).

2.4.2. Representación del problema de las 4 reinas

  • El problema se representa mediante las relaciones estado_inicial/1, estado_final/1 y sucesor/2 definidas a continuación.

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial([]).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(E) :-
   length(E,4).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(E,[Y|E]) :-
   member(Y,[1,2,3,4]),
   not(member(Y,E)),
   no_ataca(Y,E).

  • no_ataca(Y,E) se verifica si E=[Yn,...,Y1], entonces la reina colocada en (n+1,Y) no ataca a las colocadas en (1,Y1), …, (n,Yn). 

    no_ataca(Y,E) :-
   no_ataca(Y,E,1).
no_ataca(_,[],_).
no_ataca(Y,[Y1|L],D) :-
   Y1-Y =\= D,
   Y-Y1 =\= D,
   D1 is D+1,
   no_ataca(Y,L,D1).
  • El código del problema de las 4 reinas se encuentra en p_4_reinas.pl.

2.5. Solución del problema de las 4 reinas por búsqueda en profundidad sin ciclos.

  • La solución es 

    ?- [p_4_reinas, b_profundidad_sin_ciclos].
true.

?- profundidad_sin_ciclos(S).
S = [[], [2], [4, 2], [1, 4, 2], [3, 1, 4, 2]]

3. Búsqueda en profundidad con ciclos

3.1. El problema del grafo

3.1.1. Descripción del problema del grafo

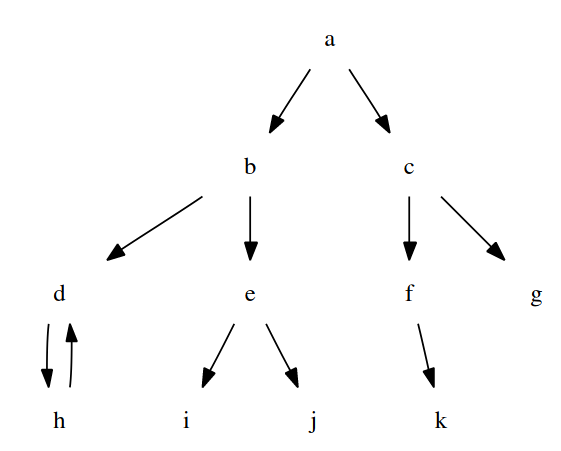
  • El problema del grafo consiste en encontrar caminos (desde a hasta f o j) en el siguiente grafo
    tema-8-grafo.png

3.1.2. Representación del problema del grafo

  • El problema se representa mediante las relaciones estado_inicial/1, estado_final/1 y sucesor/2 definidas a continuación.

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial(a).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(f).
estado_final(j).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(a,b).
sucesor(a,c).
sucesor(b,d).
sucesor(b,e).
sucesor(c,f).
sucesor(c,g).
sucesor(d,h).
sucesor(e,i).
sucesor(e,j).
sucesor(f,k).
sucesor(h,d).
  • El código del problema del grafo se encuentra en p_grafo.pl.

3.2. No solución del problema del grafo mediante búsqueda en profundidad sin ciclos

  • El problema del grafo no se puede resolver mediante búsqueda en profundidad sin ciclos. 

    ?- [p_grafo, b_profundidad_sin_ciclos].
true.

?- trace(estado_final,+call).
true.

?- profundidad_sin_ciclos(S).
 T Call: estado_final(a)
 T Call: estado_final(b)
 T Call: estado_final(d)
 T Call: estado_final(h)
 T Call: estado_final(d)
 T Call: estado_final(h)
 ...

3.3. Procedimiento de búsqueda en profundidad con ciclos

  • Un nodo es una lista de estados [E(n),...,E(1)] de forma que E(1) es el estado inicial y E(i+1) es un sucesor de E(i).

  • profundidad_con_ciclos(?S) se verifica si S es una solución del problema mediante búsqueda en profundidad con ciclos. 

    profundidad_con_ciclos(S) :-
   estado_inicial(E),
   profundidad_con_ciclos([E],S).

  • profundidad_con_ciclos(+N,?S) se verifica si S es una solución del problema a partir del nodo N (es decir S = [E(1),...,E(m)] donde N = [E(j),E(j-1),...,E(1)], E(n) es un estado final y E(i+1) es un sucesor de E(i)), encontrada por búsqueda en profundidad; es decir, mediante el siguiente procedimiento:

    • 1. Si el primer elemento de N es un estado final, entonces S es la inversa de N.
    • 2. Si N = [E|C] y E1 un sucesor de E que no ha sido visitado (es decir, que no pertenece a C) y tal que existe una solución, S, a partir de [E1,E|C].
    profundidad_con_ciclos([E|C],S) :-
   estado_final(E),
   reverse([E|C],S).
profundidad_con_ciclos([E|C],S) :-
   sucesor(E,E1),
   not(memberchk(E1,C)),
   profundidad_con_ciclos([E1,E|C],S).
  • El código de la búsqueda en profundidad con ciclos se encuentra en b_profundidad_con_ciclos.pl.

3.4. Solución del problema del grafo mediante búsqueda en profundidad con ciclos

  • Solución 

    ?- [p_grafo, b_profundidad_con_ciclos].
true.

?- profundidad_con_ciclos(S).
S = [a, b, e, j] ;
S = [a, c, f] ;
false.

?- trace(estado_final,+call).
%         estado_final/1: [call]
true.

?- profundidad_con_ciclos(S).
 T Call: estado_final(a)
 T Call: estado_final(b)
 T Call: estado_final(d)
 T Call: estado_final(h)
 T Call: estado_final(e)
 T Call: estado_final(i)
 T Call: estado_final(j)
S = [a, b, e, j] ;
 T Call: estado_final(c)
 T Call: estado_final(f)
S = [a, c, f] ;
 T Call: estado_final(k)
 T Call: estado_final(g)
false.

3.5. El problema de las jarras

3.5.1. Descripción del problema de las jarras

En el problema de las jarras

  • Se tienen dos jarras, una de 4 litros de capacidad y otra de 3.
  • Ninguna de ellas tiene marcas de medición.
  • Se tiene una bomba que permite llenar las jarras de agua.
  • El problema consiste en averiguar cómo se puede lograr tener exactamente 2 litros de agua en la jarra de 4 litros de capacidad.

3.5.2. Representación del problema de las jarras

  • El estado inicial es 0-0.

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial(0-0).
  • Los estados finales son de la forma 2-y

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(2-_).
  • Los operadores:
    • Llenar la jarra de 4 litros con la bomba.
    • Llenar la jarra de 3 litros con la bomba.
    • Vaciar la jarra de 4 litros en el suelo.
    • Vaciar la jarra de 3 litros en el suelo.
    • Llenar la jarra de 4 litros con la jarra de 3 litros.
    • Llenar la jarra de 3 litros con la jarra de 4 litros.
    • Vaciar la jarra de 3 litros en la jarra de 4 litros.
    • Vaciar la jarra de 4 litros en la jarra de 3 litros.

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(X-Y,4-Y) :-
   X < 4.
sucesor(X-Y,X-3) :-
   Y < 3.
sucesor(X-Y,0-Y) :-
   X > 0.
sucesor(X-Y,X-0) :-
   Y > 0.
sucesor(X1-Y1,4-Y2) :-
   X1 < 4,
   T is X1+Y1,
   T >= 4,
   Y2 is Y1-(4-X1).
sucesor(X1-Y1,X2-3) :-
   Y1 < 3,
   T is X1+Y1,
   T >= 3,
   X2 is X1-(3-Y1).
sucesor(X1-Y1,X2-0) :-
   Y1 > 0,
   X2 is X1+Y1,
   X2 < 4.
sucesor(X1-Y1,0-Y2) :-
   X1 > 0,
   Y2 is X1+Y1,
   Y2 < 3.
  • El código del problema de las jarras se encuentra en p_jarras.pl.

3.6. Solución del problema de las jarras por búsqueda en profundidad con ciclos

  • Solución 

    ?- [p_jarras, b_profundidad_con_ciclos].
true.

?- profundidad_con_ciclos(S).
S = [0-0,4-0,4-3,0-3,3-0,3-3,4-2,0-2,2-0] ;
S = [0-0,4-0,4-3,0-3,3-0,3-3,4-2,0-2,2-0,2-3] ;
S = [0-0,4-0,1-3,4-3,0-3,3-0,3-3,4-2,0-2,2-0]

4. Búsqueda en anchura

4.1. El problema del paseo

4.1.1. Descripción del problema del paseo

  • Una persona puede moverse en línea recta dando cada vez un paso hacia la derecha o hacia la izquierda. Podemos representarlo mediante su posición X. El valor inicial de X es 0. El problema consiste en llegar a la posición -3.

4.1.2. Representación del problema del paseo

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial(0).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(-3).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(E1,E2) :- E2 is E1+1.
sucesor(E1,E2) :- E2 is E1-1.
  • El código del problema del paseo se encuentra en p_paseo.pl.

4.2. No solución del problema del paseo mediante búsqueda en profundidad

  • El problema del paseo no se puede solucionar mediante búsqueda en profundidad con ciclos. 

    ?- [p_paseo, b_profundidad_con_ciclos].
true.

?- trace(estado_final,+call).
true.

?- profundidad_con_ciclos(S).
 T Call: estado_final(0)
 T Call: estado_final(1)
 T Call: estado_final(2)
 T Call: estado_final(3)
 T Call: estado_final(4)
 ...

4.3. Procedimiento de búsqueda en anchura

  • Un nodo es una lista de estados [E(n),...,E(1)] de forma que E(1) es el estado inicial y E(i+1) es un sucesor de E(i).
  • Abiertos es la lista de nodos pendientes de analizar.

  • anchura(?S) se verifica si S es una solución del problema mediante búsqueda en anchura. 

    anchura(S) :-
   estado_inicial(E),
   anchura([[E]],S).

  • anchura(+Abiertos,?S) se verifica si S es la solucion encontrada por búsqueda en anchura a partir de la lista de Abiertos; es decir, mediante el siguiente procedimiento:

    • 1. Si
      • 1.1. el primer elemento de Abiertos es [E|C] y
      • 1.2. E es un estado final, entonces
      • 1.3. S es la inversa de [E|C].
    • 2. Si
      • 2.1. Abiertos es la lista [[E|C]|R],
      • 2.2. la lista de los sucesores de E que no están en C ni en Abiertos es Sucesores y
      • 2.3. los nuevos abiertos, NAbiertos, es la lista obtenida añadiendo dichos Sucesores4 a continuación de ~R, entonces
      • 2.4. S es la solución obtenida por búsqueda en anchura con los nuevos abiertos.
    anchura([[E|C]|_],S) :-           % 1.1
   estado_final(E),               % 1.2
   reverse([E|C],S).              % 1.3
anchura([N|R],S) :-
   expande([N|R],Sucesores),      % 2.2
   append(R,Sucesores,NAbiertos), % 2.3
   anchura(NAbiertos,S).          % 2.4

  • expande(+Abiertos,?Sucesores) se verifica si Sucesores es la lista de los sucesores del primer elemento de Abiertos que no pertenecen al camino que lleva a dicho elemento ni a Abiertos. 

    expande([[E|C]|R],Sucesores) :-
   findall([E1,E|C],
           (sucesor(E,E1),
            not(memberchk(E1,C)),
            not(memberchk([E1|_],[[E|C]|R]))),
           Sucesores).
  • El código del procedimiento de búsqueda en anchura se encuentra en b_anchura.pl.

4.4. Solución del problema del paseo mediante búsqueda en anchura.

  • La solución es 

    ?- [p_paseo, b_anchura].
true.

?- true.

?- [p_paseo, b_anchura].
true.

?- anchura(S).
S = [0,-1,-2,-3] 
?- trace(estado_final,+call).
true.

?- anchura(S).
 T Call: estado_final(0)
 T Call: estado_final(1)
 T Call: estado_final(-1)
 T Call: estado_final(2)
 T Call: estado_final(-2)
 T Call: estado_final(3)
 T Call: estado_final(-3)
S = [0,-1,-2,-3]

5. Búsqueda óptima (de menor coste)

5.1. Problema del viaje

5.1.1. Descripción del problema del viaje:

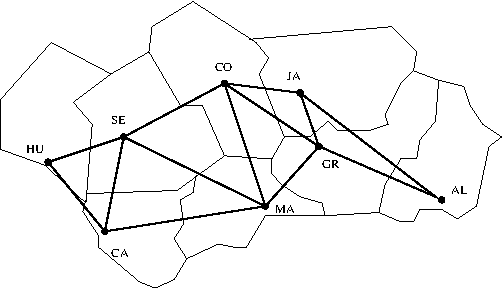
  • Nos encontramos en una capital andaluza (p.e. Sevilla) y deseamos ir a otra capital andaluza (p.e. Almería). Los autobuses sólo van de cada capital a sus vecinas, como se muestra en el siguiente mapa
    tema-8-andalucia.png

5.1.2. Representación del problema del viaje

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial(sevilla).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(almería).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(E1,E2) :-
   ( conectado(E1,E2) ; conectado(E2,E1) ).

  • conectado(?E1,?E2) se verifica si E1 y E2 están conectados. 

    conectado(huelva,sevilla).
conectado(huelva,cádiz).
conectado(sevilla,córdoba).
conectado(sevilla,málaga).
conectado(sevilla,cádiz).
conectado(córdoba,jaén).
conectado(córdoba,granada).
conectado(córdoba,málaga).
conectado(cádiz,málaga).
conectado(málaga,granada).
conectado(jaén,granada).
conectado(granada,almería).

  • coste(+E1,+E2,?C) se verifica si C es la distancia entre E1 y E2. 

    coste(E1,E2,C) :-
   coordenadas(E1,P1),
   coordenadas(E2,P2),
   distancia(P1,P2,C).

  • coordenadas(E,C) se verifica si C son las coordenadas de E según la siguiente tabla:

    almería 409.5 93
    cádiz 63 57
    córdoba 198 207
    granada 309 127.5
    huelva 3 139.5
    jaén 295.5 192
    málaga 232.5 75
    sevilla 90 153 
    coordenadas(almería, [409.5,  93  ]).
coordenadas(cádiz,   [ 63  ,  57  ]).
coordenadas(córdoba, [198  , 207  ]).
coordenadas(granada, [309  , 127.5]).
coordenadas(huelva,  [  3  , 139.5]).
coordenadas(jaén,    [295.5, 192  ]).
coordenadas(málaga,  [232.5,  75  ]).
coordenadas(sevilla, [ 90  , 153  ]).

  • distancia(+E1,+E2,?D) se verifica si D es la distancia de E1 a E2. 

    distancia([X1,Y1],[X2,Y2],D) :-
   D is sqrt((X1-X2)**2+(Y1-Y2)**2).
  • El código del problema del viaje se encuentra en p_viaje.pl.

5.2. Solución del problema del viaje mediante búsqueda en profundidad y en anchura

  • La solución es 

    ?- [p_viaje, b_profundidad_con_ciclos, b_anchura].
true.

?- profundidad_con_ciclos(S).
S = [sevilla,córdoba,jaén,granada,almería]

?- anchura(S).
S = [sevilla,córdoba,granada,almería]

5.3. Primer procedimiento de búsqueda óptima

  • óptima_1(?S) se verifica si S es una solución óptima del problema; es decir, S es una solución del problema y no hay otra solución de menor coste. 

    óptima_1(S) :-
   profundidad_con_ciclos(S),
   coste_camino(S,C),
   not((profundidad_con_ciclos(S1),
        coste_camino(S1,C1),
        C1 < C)).

  • coste_camino(+L,?C) se verifica si C es el coste del camino L. 

    coste_camino([E2,E1],C) :-
   coste(E2,E1,C).
coste_camino([E2,E1|R],C) :-
   coste(E2,E1,C1),
   coste_camino([E1|R],C2),
   C is C1+C2.
  • El código del primer procedimiento de búsqueda óptima se encuentra en b_optima_1.pl.

5.4. Solución del problema del viaje mediante búsqueda óptima

  • La solución (y la comparaciones con las anteriores) es 

    ?- [p_viaje, b_profundidad_con_ciclos, b_anchura, b_optima_1].
true.

?- óptima_1(S), b_optima_1:coste_camino(S,C).
S = [sevilla,málaga,granada,almería],
C = 361.48952882676883 

?- profundidad_con_ciclos(S), b_optima_1:coste_camino(S,C).
S = [sevilla,córdoba,jaén,granada,almería],
C = 391.54918146974836 

?- anchura(S), b_optima_1:coste_camino(S,C).
S = [sevilla,córdoba,granada,almería],
C = 363.537398328421

5.5. Segundo procedimiento de búsqueda óptima

  • Un nodo es un término de la forma C-[E(n),...,E(1)] tal que E(1) es el estado inicial, E(i+1) es un sucesor de E(i) y C es el coste de dicho camino.

  • óptima(?S) se verifica si S es una solución del problema mediante búsqueda óptima; es decir, S es la solución obtenida por búsqueda óptima a partir de [0-[E]], donde E el estado inicial. 

    óptima(S) :-
   estado_inicial(E),
   óptima([0-[E]],S).

  • óptima(+Abiertos,?S) se verifica si S es una solución del problema a partir de la lista de nodos Abiertos encontrada por búsqueda óptima. El procedimiento es

    • 1. Si
      • 1.1 C-[E|R] es el primer elemento de Abiertos y
      • 1.2 E es un estado final, entonces
      • 1.3 S es la inversa de [E|R] y el coste de S es C.
    • 2. Si N es el mejor nodo de Abiertos y RAbiertos son los restantes;
      • 2.1 Sucesores son los nodos sucesores de N (es decir, si N = C-[E|R], entonces Sucesores son los nodos de la forma C1-[E1,E|R] donde E1 es un sucesor de E que no pertenece a [E|R] y C1 es la suma de C y el coste de E a E1),
      • 2.2 Abiertos1 es la lista obtenida añadiendo Sucesores a continuación de RAbiertos y
      • 2.3 Abiertos2 es la lista obtenida ordenando Abiertos1; entonces
      • 2.4 S es la solución encontrada por búsqueda óptima a partir de Abiertos2.
    óptima([_C-[E|R]|_RA],S) :-
   estado_final(E),                       % 1.2
   reverse([E|R],S).                      % 1.3
óptima([N|RAbiertos],S) :-
   expande(N,Sucesores),                  % 2.2
   append(RAbiertos,Sucesores,Abiertos1), % 2.3
   sort(Abiertos1,Abiertos2),             % 2.4
   óptima(Abiertos2,S).                   % 2.5

  • expande(+N,?Sucesores) se verifica si Sucesores es la lista de sucesores del nodo N (es decir, si N=C-[E|R], entonces Sucesores son los nodos de la forma C1-[E1,E|R] donde E1 es un sucesor de E que no pertenece a [E|R] y C1 es la suma de C y el coste de E a E1). 

    expande(C-[E|R],Sucesores) :-
   findall(C1-[E1,E|R],
           (sucesor(E,E1),
            not(member(E1,[E|R])),
            coste(E,E1,C2),
            C1 is C+C2),
           Sucesores).
  • El código del segundo procedimiento de búsqueda óptima se encuentra en b_optima_2.pl.

5.6. Comparación de procedimientos de búsqueda óptima

  • Las comparaciones son 

    ?- [p_viaje, b_optima_1].
true.

?- time(óptima_1(S)).
% 2,458 inferences, 0.000 CPU in 0.000 seconds (100% CPU, 7720577 Lips)
S = [sevilla,málaga,granada,almería] 

?- [p_viaje, b_optima_2].
true.

?- time(óptima(S)).
% 1,487 inferences, 0.001 CPU in 0.001 seconds (100% CPU, 1310784 Lips)
S = [sevilla,málaga,granada,almería]

6. Búsqueda en escalada (con heurística).

  • La heurística de un estado es una estimación del mínimo coste de las soluciones a partir de dicho estado.
  • Un nodo es un término de la forma H-[E(n),...,E(1)] donde [E_n,…,E_1] es una lista de estados de forma que E_1 es el estado inicial y E_(i+1) es un sucesor de E_i y H es la heurística de E_n.

  • escalada(?S) se verifica si S es una solución del problema mediante búsqueda en escalada. El procedimiento es:

    • Sea E el estado inicial y H su heurística. La solución S es la solución obtenida por búsqueda en escalada a partir de H-[E].
    escalada(Sol) :-
   estado_inicial(E),
   heuristica(E,H),
   escalada(H-[E],Sol).

  • escalada(+N,?S) se verifica si S es una solución del problema a partir del nodo N encontrada por búsqueda en escalada. El procedimiento es

    • 1. Si N = H-[E|R] y
      • 1.1 E es un estado final, entonces
      • 1.2 S es la inversa de [E|R].
    • 2. Si N = H-[E|C] y
      • 2.1 E1 es un sucesor de E con heurística H1 < H y E no tiene sucesores con heurística menor que H1, entonces
      • 2.2 S es la solución por escalada a partir de H1-[E1,E|R].
    escalada(_H-[E|R],S) :-
   estado_final(E),          % 1.1
   reverse([E|R],S).         % 1.2
escalada(H-[E|R],S) :-
   mejor_sucesor(E,H,E1,H1), % 2.1
   escalada(H1-[E1,E|R],S).  % 2.2

mejor_sucesor(E,H,E1,H1) :-
   sucesor(E,E1),
   heuristica(E1,H1),
   H1 < H,
   not((sucesor(E,E2),
        heuristica(E2,H2),
        H2 < H1)).

6.1. Heurística del problema del viaje

  • heuristica(E,H) se verifica si H4 es la heurística de ~E (es decir, la distancia de E al estado final). 

    heuristica(E,H) :-
   estado_final(E1),
   coste(E,E1,H).

6.2. Solución del problema del viaje mediante búsqueda en Escalada

  • La solución es 

    ?- [p_viaje, b_escalada].
true.

?- escalada(S).
S = [sevilla,málaga,granada,almería] 

?- trace(escalada,+call).
true.

?- escalada(S).
 T Call: b_escalada:escalada(_8632)
 T Call: b_escalada:escalada(325.08498888752155-[sevilla],_8632)
 T Call: b_escalada:escalada(177.91290003819284-[málaga,sevilla],_8632)
 T Call: b_escalada:escalada(106.25676449054902-[granada,málaga,sevilla],_8632)
 T Call: b_escalada:escalada(0.0-[almería,granada,málaga,sevilla],_8632)
S = [sevilla,málaga,granada,almería]

7. Búsqueda por primero el mejor

7.1. Problema de las fichas

7.1.1. Descripción del problema de las fichas

Se considera un tablero con 7 cuadrados consecutivos. Inicialmente, en cada uno de los 3 primeros cuadrados hay una ficha blanca y en cada uno de los 3 últimos cuadrados hay una ficha verde. El objetivo consiste en tener las fichas verdes al principiocipio y las blancas al final.

La situación inicial es 

+---+---+---+---+---+---+---+
| B | B | B |   | V | V | V |
+---+---+---+---+---+---+---+

y la final es 

+---+---+---+---+---+---+---+
| V | V | V |   | B | B | B |
+---+---+---+---+---+---+---+

Los movimientos permitidos consisten en desplazar una ficha al hueco saltando, como máximo, sobre otras dos.

7.1.2. Representación del problema de las Fichas

  • Un estado es una lista de siete elementos representando cada una de las fichas (B = blanca, V = verde) y el hueco (H).

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial([b,b,b,h,v,v,v]).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final([v,v,v,h,b,b,b]).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. Por ejemplo, 

    ?- sucesor([v, v, v, h, b, b, b],E).
E = [v, v, h, v, b, b, b] ;
E = [v, h, v, v, b, b, b] ;
E = [h, v, v, v, b, b, b] ;
E = [v, v, v, b, h, b, b] ;
E = [v, v, v, b, b, h, b] ;
E = [v, v, v, b, b, b, h] ;
No

    Su definición es 

    sucesor(E1,E2) :-
   descompone(I,[F,h],D,E1),
   compone(I,[h,F],D,E2).
sucesor(E1,E2) :-
   descompone(I,[F,G,h],D,E1),
   compone(I,[h,G,F],D,E2).
sucesor(E1,E2) :-
   descompone(I,[F,G,H,h],D,E1),
   compone(I,[h,G,H,F],D,E2).
sucesor(E1,E2) :-
   descompone(I,[h,F],D,E1),
   compone(I,[F,h],D,E2).
sucesor(E1,E2) :-
   descompone(I,[h,G,F],D,E1),
   compone(I,[F,G,h],D,E2).
sucesor(E1,E2) :-
   descompone(I,[h,G,H,F],D,E1),
   compone(I,[F,G,H,h],D,E2).

  • descompone(?L1,?L2,?L3,+L4) se verifica si L4 es la concatenación de las listas L1, L2 y L3. 

    descompone(L1,L2,L3,L4) :-
   append(L12,L3,L4),
   append(L1,L2,L12).

  • compone(+L1,+L2,+L3,?L4) se verifica si L4 es la concatenación de las listas L1, L2 y L3. 

    compone(L1,L2,L3,L4) :-
   append(L1,L2,L12),
   append(L12,L3,L4).

  • Se considera la heurística que para cada estado vale la suma de piezas blancas situadas a la izquierda de cada una de las piezas verdes. Por ejemplo, para el estado 

    +---+---+---+---+---+---+---+
| B | V | B |   | V | V | B |
+---+---+---+---+---+---+---+

    su valor es 1+2+2 = 5.

  • heuristica(E,H) se verifica si H es la heurística del estado E. 

    heuristica([v|R],H) :-
   heuristica(R,H).
heuristica([h|R],H) :-
   heuristica(R,H).
heuristica([b|R],H) :-
   heuristica(R,H1),
   verdes(R,N),
   H is N+H1.
heuristica([],0).

verdes([v|R],N) :-
   verdes(R,N1),
   N is N1+1.
verdes([h|R],N) :-
   verdes(R,N).
verdes([b|R],N) :-
   verdes(R,N).
verdes([],0).
  • El código del problema de las fichas se encuentra en p_fichas.pl.

7.2. Procedimiento de búsqueda por primero el mejor

  • Un nodo es un término H-[E(n),...,E(1)] de forma que E(1) es el estado inicial, E(i+1) es un sucesor de E(i) y H es la heurística de E(n).
  • Abiertos es una lista de nodos (los nodos pendientes de analizar).
  • Cerrados es una lista de estados (los estados analizados).

  • primero_el_mejor(?S) se verifica si S es una solución del problema mediante búsqueda por primero el mejor. El procedimiento es

    1. Sea E el estado inicial y
    2. H la heurística de E.
    3. La solución S es la obtenida por búsqueda por primero el mejor con [H-[E]] como la lista de abiertos y [] como la lista de cerrados.
    primero_el_mejor(S) :-
   estado_inicial(E),               % 1
   heuristica(E,H),                 % 2
   primero_el_mejor([H-[E]],[ ],S). % 3

  • primero_el_mejor(+Abiertos,+Cerrados,?Solucion) se verifica si Solucion es la solución encontrada por búsqueda por primero el mejor a partir de las listas Abiertos y Cerrados. El procedimiento es

    • 1.1. Si el primer elemento de Abiertos es _-[E|C] y
    • 1.2. E es un estado final, entonces
    • 1.3. S es la inversa de [E|C].
    • 2.1. Si Abiertos es la lista [_-[E|_]|R],
    • 2.2. la lista de los sucesores de E que no están ni en Abiertos ni en Cerrados es Sucesores,
    • 2.3. los nuevos abiertos, NAbiertos1, es la lista obtenida añadiendo dichos Sucesores a continuación de R,
    • 2.4. la lista ordenada de los nuevos abiertos es NAbiertos y
    • 2.5. los nuevos cerrados, NCerrados, es la lista obtenida añadiendo E a Cerrados, entonces
    • 2.6. S es la solución obtenida por búsqueda primero el mejor con los nuevos abiertos y los nuevos cerrados.
    primero_el_mejor(Abiertos,_,S) :-
   Abiertos = [_-[E|C]|_],                  % 1.1
   estado_final(E),                         % 1.2
   reverse([E|C],S).                        % 1.3
primero_el_mejor(Abiertos,Cerrados,S) :-
   Abiertos = [_-[E|_]|R],                  % 2.1
   expande(Abiertos,Cerrados,Sucesores),    % 2.2
   append(R,Sucesores,NAbiertos1),          % 2.3
   sort(NAbiertos1,NAbiertos),              % 2.4
   NCerrados = [E|Cerrados],                % 2.5
   primero_el_mejor(NAbiertos,NCerrados,S). % 2.6

  • expande(+Abiertos,+Cerrados,?Sucesores) se verifica si Sucesores es la lista de los sucesores del primer elemento de Abiertos que no pertenecen si a Abiertos ni a Cerrados. 

    expande(Abiertos,Cerrados,Sucesores) :-
   Abiertos = [_-[E|C]|_],
   findall(H1-[E1,E|C],
           (sucesor(E,E1),
            not(memberchk(_-[E1|_],Abiertos)),
            not(memberchk(E1,Cerrados)),
            heuristica(E1,H1)),
           Sucesores).
  • El código de la búsqueda por primero el mejor se encuentra em b_primero_mejor.pl.

7.3. Solución del problema de las fichas mediante búsqueda por primero el mejor

  • La solución es 

    ?- [p_fichas, b_primero_mejor].
true.

?- primero_el_mejor(S).
S = [[b,b,b,h,v,v,v],
     [b,b,b,v,h,v,v],
     [b,b,h,v,b,v,v],
     [b,b,v,v,b,h,v],
     [b,b,v,v,b,v,h],
     [b,b,v,v,h,v,b],
     [b,h,v,v,b,v,b],
     [b,v,h,v,b,v,b],
     [b,v,v,v,b,h,b],
     [b,v,v,v,h,b,b],
     [b,v,h,v,v,b,b],
     [h,v,b,v,v,b,b],
     [v,v,b,h,v,b,b],
     [v,v,b,v,h,b,b],
     [v,v,h,v,b,b,b],
     [v,v,v,h,b,b,b]]

8. Algoritmo A*

8.1. El problema del 8 puzzle

8.1.1. Descripción del problema del 8 puzzle

8.1.2. Representación del problema del 9 puzzle

  • Un estado es una lista de los elementos del tablero de arriba a abajo y de izquierda a derecha.

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial([2,8,3,1,6,4,7,h,5]).

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final([1,2,3,8,h,4,7,6,5]).

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(E1,E2) :-
   operador(O),
   transforma(E1,O,E2).

  • operador(O) se verifica si O es un operador. 

    operador(izquierda). % Mover hueco a la izquierda
operador(arriba).    % Mover hueco arriba
operador(derecha).   % Mover hueco a la derecha
operador(abajo).     % Mover hueco abajo

  • transforma(+E1,+O,?E2) se verifica si E2 es el estado obtenido aplicándole a E1 el operador O. 

    transforma(E1,izquierda,E2) :-
   el_hueco_no_esta_en_la_primera_columna(E1),
   descompone(I,[A,h],D,E1),
   compone(I,[h,A],D,E2).
transforma(E1,arriba,E2) :-
   descompone(I,[A,B,C,h],D,E1),
   compone(I,[h,B,C,A],D,E2).
transforma(E1,derecha,E2) :-
   el_hueco_no_esta_en_la_ultima_columna(E1),
   descompone(I,[h,A],D,E1),
   compone(I,[A,h],D,E2).
transforma(E1,abajo,E2) :-
   descompone(I,[h,A,B,C],D,E1),
   compone(I,[C,A,B,h],D,E2).

  • el_hueco_no_esta_en_la_primera_columna(E) se verifica si en el estado E, el hueco no está en la primera columna. 

    el_hueco_no_esta_en_la_primera_columna(E) :-
   nth0(N,E,h),
   N mod 3 =\= 0.

  • el_hueco_no_esta_en_la_ultima_columna(E) se verifica si en el estado E, el hueco no está en la ultima columna. 

    el_hueco_no_esta_en_la_ultima_columna(E) :-
   nth0(N,E,h),
   N mod 3 =\= 2.

  • descompone(?L1,?L2,?L3,+L4) se verifica si L4 es la concatenación de las listas L1, L2 y L3. 

    descompone(L1,L2,L3,L4) :-
   append(L12,L3,L4),
   append(L1,L2,L12).

  • compone(+L1,+L2,+L3,?L4) se verifica si L4 es la concatenación de las listas L1, L2 y L3. 

    compone(L1,L2,L3,L4) :-
   append(L1,L2,L12),
   append(L12,L3,L4).

  • heuristica(+E,?H) se verifica si H es el número de piezas colocadas en E en distinto lugar que en el estado final. 

    heuristica(E,H) :-
   estado_final(EF),
   diferencias(E,EF,H).

  • diferencias(+L1,+L2,?D) se verifica si D es el número de elementos de la lista L1 distintos de los correspondientes en L2. 

    diferencias([X|R1],[Y|R2],D) :-
   diferencias(R1,R2,D1),
   ( (X==h; X==Y) -> D is D1
   ; otherwise    -> D is D1+1).
diferencias([],[],0).

  • coste(+E1,+E2,?C) se verifica si C es el coste de pasar de E1 a E2. En este caso, todos los costes valen 1. 

    coste(_,_,1).
  • El código del 8 puzzle se encuentra en p_8_puzzle.pl.

8.2. El algoritmo A*

  • Un nodo es un término de la forma F/C-[E(n),...,E(1)] donde [E(n),...,E(1)] es una lista de estados de forma que E(1) es el estado inicial y E(i+1) es un sucesor de E(i), C es el coste de dicho camino y F es la suma de C y la heurística de E(n).
  • Abiertos es una lista de nodos.

  • a_estrella(?S) se verifica si S es una solución del problema mediante A*. El procedimiento es

    • Sea E el estado inicial y H su heurística. La solución S es la solución obtenida por A* a partir de [H/0-[E]].
    a_estrella(S) :-
   estado_inicial(E),
   heuristica(E,H),
   a_estrella([H/0-[E]],S).

  • a_estrella(+Abiertos,?S) se verifica si S es una solución del problema a partir de Abiertos mediante A*. El procedimiento es

    • 1. Si _-[E|C] es el mejor nodo de Abiertos y
      • 1.1 E es un estado final, entonces
      • 1.2 S es la inversa de [E|C].
    • 2. Si N es el mejor nodo de Abiertos y R son los restantes;
      • 2.1 Sucesores son los sucesores de E que no están en su camino,
      • 2.2 NAbiertos1 es la lista obtenida añadiendo Sucesores a continuación de R y
      • 2.3 NAbiertos2 es la lista obtenida ordenando NAbiertos1; entonces
      • 2.4 S es la solución encontrada por búsqueda minimal a partir de Nodos2 y Co es su coste.
    a_estrella([_-[E|C]|_],S) :-
   estado_final(E),                % 1.1
   reverse([E|C],S).               % 1.2
a_estrella([N|R],S) :-
   expande(N,Sucesores),           % 2.1
   append(R,Sucesores,NAbiertos1), % 2.2
   sort(NAbiertos1,NAbiertos2),    % 2.3
   a_estrella(NAbiertos2,S).       % 2.4

  • expande(+N,?Sucs) se verifica si Sucs es la lista de sucesores del nodo N que no han sido visitados (es decir, los sucesores del primer elemento de N que no pertenecen al resto de N). 

    expande(_/C-[E|R],Sucs) :-
   findall(F1/C1-[E1,E|R],
           (sucesor(E,E1),
            not(member(E1,R)),
            coste(E,E1,C2),
            C1 is C+C2,
            heuristica(E1,H1),
            F1 is C1+H1),
           Sucs).
  • El código del algoritmo A* se encuentra en b_a_estrella.pl.

8.3. Solucióm del 8 puzzle mediante el algoritmo A*

  • La solución es 

    ?- [p_8_puzzle, b_a_estrella].
true.

?- a_estrella(S).
S = [[2,8,3,1,6,4,7,h,5],
     [2,8,3,1,h,4,7,6,5],
     [2,h,3,1,8,4,7,6,5],
     [h,2,3,1,8,4,7,6,5],
     [1,2,3,h,8,4,7,6,5],
     [1,2,3,8,h,4,7,6,5]] 

?- trace(expande, +call).
true.

?- a_estrella(S).
 T Call: b_a_estrella:expande(4/0-[[2,8,3,1,6,4,7,h,5]],_5016)
 T Call: b_a_estrella:expande(4/1-[[2,8,3,1,h,4,7,6,5],
                                   [2,8,3,1,6,4,7,h,5]],_5996)
 T Call: b_a_estrella:expande(5/2-[[2,8,3,h,1,4,7,6,5],
                                   [2,8,3,1,h,4,7,6,5],
                                   [2,8,3,1,6,4,7,h,5]],_7108)
 T Call: b_a_estrella:expande(5/2-[[2,h,3,1,8,4,7,6,5],
                                   [2,8,3,1,h,4,7,6,5],
                                   [2,8,3,1,6,4,7,h,5]],_8142)
 T Call: b_a_estrella:expande(5/3-[[h,2,3,1,8,4,7,6,5],
                                   [2,h,3,1,8,4,7,6,5],
                                   [2,8,3,1,h,4,7,6,5],
                                   [2,8,3,1,6,4,7,h,5]],_9152)
 T Call: b_a_estrella:expande(5/4-[[1,2,3,h,8,4,7,6,5],
                                   [h,2,3,1,8,4,7,6,5],
                                   [2,h,3,1,8,4,7,6,5],
                                   [2,8,3,1,h,4,7,6,5],
                                   [2,8,3,1,6,4,7,h,5]],_10006)
S = [[2,8,3,1,6,4,7,h,5],
     [2,8,3,1,h,4,7,6,5],
     [2,h,3,1,8,4,7,6,5],
     [h,2,3,1,8,4,7,6,5],
     [1,2,3,h,8,4,7,6,5],
     [1,2,3,8,h,4,7,6,5]]

9. Ejercicios

9.1. Problemas de los bloques

Ejercicio 1.1. En una mesa hay una pila de bloques y sitio para otras dos pilas: 

+---+  
| C |  
+---+  
| A |  
+---+  
| B |  
+---+    +---+    +---+

Las operaciones que se pueden realizar son:

  • Mover el bloque situado en la cima de una pila a la mesa.
  • Mover un bloque de la mesa a la cima de una pila.
  • Mover un bloque situado en la cima de una pila a la cima de otra pila.

El problema consiste en poner los bloques de la siguiente forma 

+---+  
| A |  
+---+  
| B |  
+---+  
| C |  
+---+

En la representación del problema se consideran que los estado son listas de tres elementos, cada uno de los cuales es una lista con los elementos que la forman (el primero es la cima y el último es la base).

Definir la relación estado_inicial(?E) que se verifica si E es el estado inicial.

Solución 

estado_inicial([[c,a,b],[],[]]).

Ejercicio 1.2. Definir la relación estado_final(?E) que se verifica si E es un estado final.

Solución 

estado_final(E) :-
   member([a,b,c],E).

Ejercicio 1.3. Definir la relación sucesor(+E1,?E2) que se verifica si E2 es un sucesor del estado E1.

Solución 

sucesor([[B|R],P2,P3],[R,[B|P2],P3]).
sucesor([[B|R],P2,P3],[R,P2,[B|P3]]).
sucesor([P1,[B|R],P3],[[B|P1],R,P3]).
sucesor([P1,[B|R],P3],[P1,R,[B|P3]]).
sucesor([P1,P2,[B|R]],[[B|P1],P2,R]).
sucesor([P1,P2,[B|R]],[P1,[B|P2],R]).

Ejercicio 1.4. Intentar resolver el problema mediante búsqueda en profundidad sin ciclos.

Solución Con la búsqueda en profundidad sin ciclos no se encuentra solución. 

?- [b_profundidad_sin_ciclos].
true.

?- trace(estado_final,+call).
true.

?- profundidad_sin_ciclos(S).
 T Call: estado_final([[c,a,b],[],[]])
 T Call: estado_final([[a,b],[c],[]])
 T Call: estado_final([[b],[a,c],[]])
 T Call: estado_final([[],[b,a,c],[]])
 T Call: estado_final([[b],[a,c],[]])
 ...
?- trace(estado_final,-call).
true.

Ejercicio 1.5. Resolver el problema mediante búsqueda en profundidad con ciclos.

Solución 

?- [b_profundidad_con_ciclos].
true.

?- profundidad_con_ciclos(S).
S = [[[c,a,b], [],      []],
     [[a,b],   [c],     []],
     [[b],     [a,c],   []],
     [[],      [b,a,c], []],
     [[],      [a,c],   [b]],
     [[a],     [c],     [b]],
     [[],      [c],     [a,b]],
     [[c],     [],      [a,b]],
     [[a,c],   [],      [b]],
     [[c],     [a],     [b]],
     [[],      [c,a],   [b]],
     [[],      [a],     [c,b]],
     [[a],     [],      [c,b]],
     [[c,a],   [],      [b]],
     [[b,c,a], [],      []],
     [[c,a],   [b],     []],
     [[a],     [c,b],   []],
     [[],      [a,c,b], []],
     [[],      [c,b],   [a]],
     [[c],     [b],     [a]],
     [[],      [b],     [c,a]],
     [[b],     [],      [c,a]],
     [[c,b],   [],      [a]],
     [[b],     [c],     [a]],
     [[],      [b,c],   [a]],
     [[],      [c],     [b,a]],
     [[c],     [],      [b,a]],
     [[b,c],   [],      [a]],
     [[a,b,c], [],      []]]

Ejercicio 1.6. Resolver el problema mediante búsqueda en anchura.

Solución 

?-[b_anchura].
true.

?- anchura(S).
S = [[[c,a,b], [],      []],
     [[a,b],   [c],     []],
     [[b],     [c],     [a]],
     [[],      [b,c],   [a]],
     [[],      [a,b,c], []]]

9.2. Problema de las 8 reinas

Ejercicio 2.1. El problema de las 8 reinas consiste en colocar 8 reinas en un tablero rectangular de dimensiones 8 por 8 de forma que no se encuentren más de una en la misma línea: horizontal, vertical o diagonal.

Los estados son listas de números que representan las ordenadas de las respectivas reinas. Por ejemplo, [3,5] representa que se ha colocado las reinas (1,5) y (2,3).

Definir la relación estado_inicial(?E) que se verifica si E es el estado inicial.

Solución 

estado_inicial([]).

Ejercicio 2.2. Definir la relación estado_final(?E) que se verifica si E es un estado final.

Solución 

estado_final(E) :-
   length(E,8).

Ejercicio 2.3. Definir la relación sucesor(+E1,?E2) que se verifica si E2 es un sucesor del estado E1.

Solución 

sucesor(E,[Y|E]) :-
   member(Y,[1,2,3,4,5,6,7,8]),
   not(member(Y,E)),
   no_ataca(Y,E).

% no_ataca(Y,E) se verifica si E = [Y_n,...,Y_1] y la reina colocada en
% (n+1,Y) no ataca a las colocadas en (1,Y_1),...,(n,Y_n).
no_ataca(Y,E) :-
   no_ataca(Y,E,1).
no_ataca(_,[],_).
no_ataca(Y,[Y1|L],D) :-
   Y1-Y =\= D,
   Y-Y1 =\= D,
   D1 is D+1,
   no_ataca(Y,L,D1).

Ejercicio 2.4. Resolver el problema por búsqueda en profundidad sin ciclos.

Solución 

?- [b_profundidad_sin_ciclos].
true.

?- profundidad_sin_ciclos(S).
S = [[],
     [1],
     [5,1],
     [8,5,1],
     [6,8,5,1],
     [3,6,8,5,1],
     [7,3,6,8,5,1],
     [2,7,3,6,8,5,1],
     [4,2,7,3,6,8,5,1]]

Ejercicio 2.5. Resolver el problema por búsqueda en anchura.

Solución 

?- [b_anchura].
true.

?- anchura(S).
S = [[],
     [1],
     [5,1],
     [8,5,1],
     [6,8,5,1],
     [3,6,8,5,1],
     [7,3,6,8,5,1],
     [2,7,3,6,8,5,1],
     [4,2,7,3,6,8,5,1]]

10. Bibliografía

| Inicial | Temas | Manuales | Ejercicios | Exámenes | Documentación

José A. Alonso Jiménez

Sevilla, 07 de abril del 2024

Licencia: Creative Commons.