Tema 9: Programación lógica con restricciones

• Importación del módulo

  ?- use_module(library(clpr)).
  true.
  

• Diferencia entre objetivo y restricción:

  ?- 1 + X = 5.
  false.
  
  ?- {1 + X = 5}.
  X = 4.0 
  

• Restricciones aritméticas en CLP(R):
  • <restricciones> := {<restricción 1>, <restricción 2>, …}
  • <restricción> := <expresión 1> <operador> <expresión 2>
    donde
    • <expresión 1> y <expresión 2> son expresiones aritméticas
    • <operador> es uno de los siguientes: =, =\=, <, =<, >, >=

• Ejemplo de ecuaciones e inecuaciones:

  ?- {3 * X - 2 * Y = 6, 2 * Y = X}.
  X = 3.0,
  Y = 1.5.
  
  ?- {Z =< X - 2, X + 2 = 5}.
  X = 3.0,
  {Z=1.0-_12374,_12374>=0.0} 
  
  ?- {X > 0, X + 2 < 0}.
  false.
  

• convierte(-C,+F) se verifica si C son los grados centígrados correspondientes a F grados Fahrenheit; es decir, C = (F-32)*5/9.

• Programa Prolog

  convierte_1(C,F) :-
     C is (F-32)*5/9.
  

• Sesión con el programa Prolog

  ?- convierte_1(C,95).
  C = 35.
  
  ?- convierte_1(35,F).
  ERROR: Arguments are not sufficiently instantiated
  

• Programa CLP(R)

  :- use_module(library(clpr)).
  
  convierte_2(C,F) :-
     {C = (F-32)*5/9}.
  

• Sesión con el programa CLP(R)

  ?- convierte_2(C,95).
  C = 35.0 
  ?- convierte_2(35,F).
  F = 95.0 
  ?- convierte_2(C,F).
  {F=32.0+1.7999999999999998*C}.
  

• Optimización con minimize/1 y maximize/1:

  ?- {X =< 5}, maximize(X).
  X = 5.0 
  
  ?- {X =< 5, 2 =< X}, minimize(2 * X + 3).
  X = 2.0 
  
  ?- {3 =< X, X + 1 =< Y + 2, Y =< 9, Z = X + Y}, minimize(Z).
  X = 3.0,
  Y = 2.0,
  Z = 5.0 
  
  ?- {X + Y =< 4}, maximize(X + Y).
  {Y=4.0-X} 
  
  ?- {X =< 5}, minimize(X).
  false.
  

• Optimización con sup/2 e inf/2:

  ?- {2 =< X, X =< 5}, inf(X, I), sup(X, S).
  I = 2.0,
  S = 5.0,
  {X>=2.0,X=<5.0}
  
  ?- {3 =< X, X + 1 =< Y + 2, Y =< 9, Z = X + Y}, inf(Z, I), sup(Z, S).
  I = 5.0,
  S = 19.0,
  {Z= -1.0+2.0*X+_6360,_6360>=0.0,Y= -1.0+X+_6360,X+_6360=<10.0,X>=3.0} 
  

• Problema: Calcular el menor tiempo necesario para realizar las tareas A, B, C y D teniendo en cuenta que los tiempos empleados en cada una son 2, 3, 5 y 4, respectivamente, y además que A precede a B y a C y que B precede a D.
  

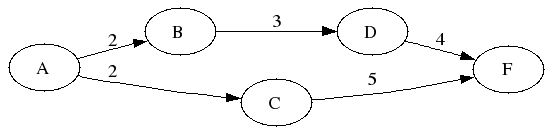
• Plan óptimo:

  ?- {Ta >= 0, Ta + 2 =< Tb, Ta + 2 =< Tc, Tb + 3 =< Td, Tc + 5 =< Tf, Td + 4 =< Tf},
     minimize(Tf).
  Ta = 0.0,
  Tb = 2.0,
  Td = 5.0,
  Tf = 9.0,
  {_9152>=0.0,_9170=2.0-_9152,_9152=<2.0,Tc=4.0-_9152} 
  

• fib(+N,-F) se verifica si F es el N-ésimo término de la sucesión de Fibonacci; es decir, 0, 1, 1, 2, 3, 5, 8, 13, 21, …

• Programa Prolog (sin restricciones)

  fib_1(N, F) :-
     ( N = 0, F = 1
     ; N = 1, F = 1
     ; N > 1,
       N1 is N - 1, fib_1(N1, F1),
       N2 is N - 2, fib_1(N2, F2),
       F is F1 + F2 ).
  

• Sesión con el programa Prolog

  ?- fib_1(6,F).
  F = 13 
  
  ?- fib_1(N,13).
  ERROR: Arguments are not sufficiently instantiated
  

• Programa CLP(R)

  :- use_module(library(clpr)).
  
  fib_2(N, F) :-
     ( {N = 0, F = 1}
     ; {N = 1, F = 1}
     ; {N > 1, F = F1 + F2, N1 = N- 1, N2 = N - 2},
       fib_2(N1, F1),
       fib_2(N2, F2) ).
  

• Sesión con el programa CLP(R)

  ?- fib_2(6, F).
  F = 13.0 
  
  ?- fib_2(N,13).
  N = 6.0 
  
  ?- fib_2(N,4).
  ERROR: Out of global stack
  

• Modificación de fib_2 para determinar los números que no son términos de la sucesión

  fib_3(N, F) :-
     ( {N = 0, F = 1}
     ; {N = 1, F = 1}
     ; {N > 1, F = F1 + F2, N1 = N - 1, N2 = N - 2, F1 >= N1, F2 >= N2},
       fib_3(N1, F1),
       fib_3(N2, F2) ).
  

• Sesión

  ?- fib_3(6,F).
  F = 13.0 
  
  ?- fib_3(N,13).
  N = 6.0 
  
  ?- fib_3(N,4).
  false.
  

• El código de las definiciones anteriores se encuentra en fibonacci_clp.pl.

• Cálculos con CLP(Q)

  ?- use_module(library(clpq)).
  true.
  
  ?- {X = 2 * Y, Y = 1 - X}.
  X = 2r3,
  Y = 1r3.
  

• Especificación de un problema mediante tareas y precede
  

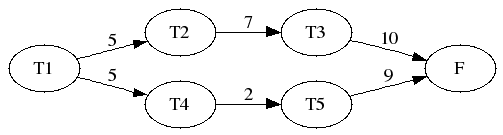
• tareas(+LTD) se verifica si LTD es la lista de los pares T/D de las tareas y sus duraciones.

  tareas([t1/5, t2/7, t3/10, t4/2, t5/9]).
  

• precede(+T1,+T2) se verifica si la tarea T1 tiene que preceder a la T2.

  precede(t1, t2).
  precede(t1, t4).
  precede(t2, t3).
  precede(t4, t5).
  

• planificación(P,TP) se verifica si P es el plan (esto es una lista de elementos de la forma tarea/inicio/duración) para realizar las tareas en el menor tiempo posible y TP es dicho tiempo. Por ejemplo,

  ?- planificación(P,TP).
  P = [t1/0/5,t2/5/7,t3/12/10,t4/_20034/2,t5/_20052/9],
  TP = 22,
  {_20084= -6-_20098-_20092,_20098+_20092>= -6,_20092=<0,_20052=13+_20098,
   _20098=<0,_20034=11+_20098+_20092,_20186= -9+_20098+_20092} 
  
  ?- planificación([_/I1/_, _/I2/_, _/I3/_, _/I4/_, _/I5/_],TP).
  I1 = 0,
  I2 = 5,
  I3 = 12,
  TP = 22,
  {_27474= -6-_27488-_27482,_27488+_27482>= -6,_27482=<0,I5=13+_27488,
   _27488=<0,I4=11+_27488+_27482,_27576= -9+_27488+_27482} 
  

  Su definición es

  planificación(P, TP) :-
     tareas(LTD),
     restricciones(LTD, P, TP),
     minimize(TP).
  

• restricciones(LTD,P,TP) se verifica si P es un plan para realizar las tareas de LTD cumpliendo las restricciones definidas por precedencia/2 y TP es el tiempo que se necesita para ejecutar el plan P.

  restricciones([],[],_TP).
  restricciones([T/D | RLTD], [T/I/D | RTID], TP) :-
     {I >= 0, I + D =< TP}, 
     restricciones(RLTD, RTID, TP),      
     restricciones_aux(T/I/D, RTID).
  

• restricciones_aux(TID,LTID) se verifica si el triple tarea-inicio-duración TID es consistente con la lista de triples tarea-inicio-duración LTID.

  restricciones_aux(_,[]).
  restricciones_aux(T/I/D, [T1/I1/D1 | RTID]) :-
     ( precede(T, T1) -> {I + D =< I1}
     ; precede(T1, T) -> {I1 + D1 =< I}
     ; true ),
     restricciones_aux(T/I/D, RTID).
  

• El código de la planificación de tareas se encuentra en planificacion.pl.

• solución([S,E,N,D],[M,O,R,E],[M,O,N,E,Y]) se verifica si cada una de las letras se sustituye por un dígito distinto de forma que SEND+MORE=MONEY. Por ejemplo,

  ?- solución(L1,L2,L3).
  L1 = [9,5,6,7],
  L2 = [1,0,8,5],
  L3 = [1,0,6,5,2] ;
  false.
  
  ?- solución([S,E,N,D],[M,O,R,E],[M,O,N,E,Y]).
  S = 9,
  E = 5,
  N = 6,
  D = 7,
  M = 1,
  O = 0,
  R = 8,
  Y = 2 ;
  false.
  

  Su definición es

  :- use_module(library(clpfd).
  
  solución_5([S,E,N,D],[M,O,R,E],[M,O,N,E,Y]) :-
     Vars = [S,E,N,D,M,O,R,Y],
     Vars ins 0..9,
     all_distinct(Vars),
             1000*S+100*E+10*N+D
           + 1000*M+100*O+10*R+E #=
     10000*M+1000*O+100*N+10*E+Y,
     M #\= 0,
     S #\= 0,
     label(Vars).
  

• El código del problema SEN+MORE=MONEY se encuentra en criptoaritmetica.pl.

• El problema de las N reinas consiste en colocar N reinas en un tablero rectangular de dimensiones N por N de forma que no se encuentren más de una en la misma línea: horizontal, vertical o diagonal.

• solución(N,L) se verifica si L es una solución del problema de las N reinas. Por ejemplo,

  ?- solución(4,L).
  L = [2,4,1,3] ;
  L = [3,1,4,2]
  
  ?- solución(8,L).
  L = [1,5,8,6,3,7,2,4] ;
  L = [1,6,8,3,7,4,2,5] 
  
  ?- findall(_S, solución(8, _S), _L), length(_L, N).
  N = 92.
  

  Su definición es

  solución(N,L) :-             
     length(L,N),     % Hay N reinas
     L ins 1..N,      % Las ordenadas están en el intervalo 1..N
     all_distinct(L), % Las ordenadas son distintas (distintas filas)
     segura(L),       % No hay en más de una en las diagonales
     label(L).        % Buscar los valores de L
  

• segura(L) se verifica si las reinas colocadas en las ordenadas L no se atacan diagonalmente.

  segura([]).
  segura([Y|L]) :-
     no_ataca(Y,L,1), 
     segura(L).
  

• no_ataca(Y,L,D) se verifica si Y es un número, L es una lista de números [n(1),...,n(m)] y D es un número tales que la reina colocada en la posición (x,Y) no ataca a las colocadas en las posiciones ~(x+d,n(1)),…,(x+d+m,n(m))}.

  no_ataca(_Y,[],_).
  no_ataca(Y1,[Y2|L],D) :-
     Y1-Y2 #\= D,
     Y2-Y1 #\= D,
     D1 is D+1,
     no_ataca(Y1,L,D1).
  

• mejor(X) restringe los valores de X a su menor valor. Por ejemplo,

  ?- X in 1..6, Y #= X*(X-6), mejor(Y).
  X = 3,
  Y = -9 
  
  ?- X in 1..6, Y #= X*(6-X), mejor(Y).
  X = 6,
  Y = 0 
  

  Su definición es

  % 1ª definición
  mejor(X) :-
     findall(X, indomain(X), L),
     member(Y, L),
     not((member(Z, L), Z < Y)),
     X #= Y.
  
  % 2ª definición
  mejor_2(X) :-
     labeling([min(X)],[X]).
  

• El código anterior se encuentra en mejor.pl.

• Problema: Calcular el tiempo necesario para realizar las tareas A, B, C y D teniendo en cuenta que los tiempos empleados en cada una son 2, 3, 5 y 4, respectivamente, y además que A precede a B y a C y que B precede a D.

  ?- [Ta,Tb,Tc,Td,Tf] ins 0..10,
     Ta+2 #=< Tb,   Ta+2 #=< Tc,   Tb+3 #=< Td,   
     Tc+5 #=< Tf,   Td+4 #=< Tf,
     findall(Ta, indomain(Ta), Da),
     findall(Tb, indomain(Tb), Db),
     findall(Tc, indomain(Tc), Dc),
     findall(Td, indomain(Td), Dd),
     findall(Tf, indomain(Tf), Df).
  Da = [0,1],
  Db = [2,3],
  Dc = [2,3,4,5],
  Dd = [5,6],
  Df = [9,10],
  Ta in 0..1,
  Ta#=<Tc+ -2,
  Ta#=<Tb+ -2,
  Tc in 2..5,
  Tc#=<Tf+ -5,
  Tf in 9..10,
  Td#=<Tf+ -4,
  Td in 5..6,
  Tb#=<Td+ -3,
  Tb in 2..3.
  

• Traza:

  Paso		Ta	Tb	Tc	Td	Tf
  		0..10	0..10	0..10	0..10	0..10
  1	Ta+2 ≤ Tb	0..8	2..10
  2	Tb+3 ≤ Td		2..7		5..10
  3	Td+4 ≤ Tf				5..6	9..10
  4	Tb+3 ≤ Td		2..3
  5	Ta+2 ≤ Tb	0..1
  6	Ta+2 ≤ Tc			2..10
  7	Tc+5 ≤ Tf			2..5

• En el problema de los músicos se sabe que

  1. Una banda está compuesta por tres músicos de distintos paises y que tocan distintos instrumentos.
  2. El pianista toca primero.
  3. Juan toca el saxo y toca antes que el cubano.
  4. Marcos es ruso y toca antes que el flautista.
  5. Hay un músico coreano.
  6. Un músico se llama Luis.

  El problema consiste en determinar el nombre, el país y el instrumento que toca cada uno de los músicos de la banda.

• El primer programa para resolver el problema de los músicos es

  :- use_module(library(clpfd)).
  
  músicos(Juan, Marco, Luis, Cuba, Rusia, Corea, Piano, Saxo, Flauta) :-
     % dominios
     [Juan, Marco, Luis, Cuba, Rusia, Corea, Piano, Saxo, Flauta] ins 1..3,
  
     % todas distintas de la de los otros:
     all_distinct([Juan, Marco, Luis]),
     all_distinct([Cuba, Rusia, Corea]),
     all_distinct([Piano, Saxo, Flauta]),
  
     % restricciones;
     Piano #=1,       % 2
     Juan #= Saxo,    % 3a
     Juan #< Cuba,    % 3b
     Marco #= Rusia,  % 4a
     Marco #< Flauta, % 4b
  
     % instancia las variables de la lista a elementos de su dominio:
     label([Juan, Marco, Luis, Cuba, Rusia, Corea, Piano, Saxo, Flauta]).
  

• El cálculo de la solución es

  ?- músicos(Juan, Marco, Luis, Cuba, Rusia, Corea, Piano, Saxo, Flauta).
  Juan = Corea, Corea = Saxo, Saxo = 2,
  Marco = Rusia, Rusia = Piano, Piano = 1,
  Luis = Cuba, Cuba = Flauta, Flauta = 3.
  

• La solución es

  	Nombre	País	Instrumento
  1	Marco	Rusia	Piano
  2	Juan	Corea	Saxo
  3	Luis	Cuba	Flauta

• El código del primer programa para resolver el problema de los músicos está en musicos_1.pl.

• El segundo programa para resolver el problema de los músicos es

  :- use_module(library(clpfd)).
  
  músicos(S) :-
     S = [Nombre, Pais, Instrumento],
     Nombre = [Juan, Marco, Luis],
     Pais = [Cuba, Rusia, Corea],
     Instrumento = [Piano, Saxo, Flauta],
  
     % L es la lista de los elementos de S:
     flatten(S, L),
  
     % dominios
     L ins 1..3,
  
     % todas distintas de la de los otros:
     all_distinct(Nombre),
     all_distinct(Pais),
     all_distinct(Instrumento),
  
     % restricciones;
     Piano #=1,          % 2
     Juan #= Saxo,       % 3a
     Juan #< Cuba,       % 3b
     Marco #= Rusia,     % 4a
     Marco #< Flauta,    % 4b
  
     % instancia las variables de la lista a elementos de su dominio:
     label(L).
  

• El cálculo de la solución es

  ?- músicos(S).
  S = [[2,1,3],[3,1,2],[1,2,3]].
  
  ?- músicos([[Juan,Marco,Luis],[Cuba,Rusia,Corea],[Piano,Saxo,Flauta]]).
  Juan = Corea, Corea = Saxo, Saxo = 2,
  Marco = Rusia, Rusia = Piano, Piano = 1,
  Luis = Cuba, Cuba = Flauta, Flauta = 3.
  

• El código del segundo programa para resolver el problema de los músicos está en musicos_2.pl.

• En el Problema de la cebra (de Lewis Carroll)
  • Se consideran cinco hombres de distintas nacionalidades viven en las cinco primeras casas de una calle. Cada uno tiene una profesión, un animal favorito y una bebida favorita (todas distintas de la de los otros).
  • Se sabe que
    • 1. El inglés vive en la casa roja.
    • 2. El español tiene un perro.
    • 3. El japonés es pintor.
    • 4. El italiano bebe té.
    • 5. El Noruego vive en la primera casa de la izquierda.
    • 6. El propietario de la casa verde bebe café.
    • 7. La casa verde está a la derecha de la blanca.
    • 8. El escultor cria caracoles.
    • 9. El diplomático vive en la casa amarilla.
    • 10. En la casa central beben leche.
    • 11. La casa del noruego está al lado de la casa azul.
    • 12. El violinista bebe zumo de fruta.
    • 13. El zorro está en la casa vecina de la del médico.
    • 14. El caballo está en la casa vecina de la del diplomático.
  • El problema consiste en determinar dónde está la cebra y quién bebe agua.

• Programa para el problema de la cebra

  :- use_module(library(clpfd)).
  
  cebra(Cebra, Agua, S) :-
     % Variables:
     S = [Nacionalidad, Color, Profesión, Animal, Bebida],
     Nacionalidad = [Inglés, Español, Japones, Italiano, Noruego],
     Color = [Roja, Verde, Blanca, Amarilla, Azul],
     Profesión = [Pintor, Escultor, Diplomático, Violinista, Doctor],
     Animal = [Perro, Caracol, Zorro, Caballo, Cebra],
     Bebida = [Te, Cafe, Leche, Zumo, Agua],
     flatten(S, L),
  
     % especificamos los dominios (el valor de cada variable es el número de la
     % casa): 
     % Nacionalidad in 1..5,
     % Color in 1..5,
     % Profesión in 1..5,
     % Animal in 1..5,
     % Bebida in 1..5,
     L ins 1..5,
  
     % todas distintas de la de los otros:
     all_distinct(Nacionalidad),
     all_distinct(Color),
     all_distinct(Profesión),
     all_distinct(Animal),
     all_distinct(Bebida),
  
     % restricciones:
     Inglés = Roja,                                      % 1
     Español = Perro,                                    % 2
     Japones = Pintor,                                   % 3
     Italiano = Te,                                      % 4
     Noruego = 1,                                        % 5
     Verde = Cafe,                                       % 6
     Verde #= Blanca + 1,                                % 7
     Escultor = Caracol,                                 % 8
     Diplomático = Amarilla,                             % 9
     Leche = 3,                                          % 10
     vecino(Noruego, Azul),                              % 11
     Violinista = Zumo,                                  % 12
     vecino(Zorro, Doctor),                              % 13
     vecino(Caballo, Diplomático),                       % 14
  
     % instancia las variables de la lista a elementos de su dominio:
     label(L).
  
  vecino(X,Y) :-
     (X #= Y+1) #\/ (X #= Y-1). 
  

• Cálculo de la solución

  ?- cebra(Cebra, Agua, S).
  Cebra = 5,
  Agua = 1,
  S = [[3,4,5,2,1],
       [3,5,4,1,2],
       [5,3,1,4,2],
       [4,3,1,2,5],
       [2,5,3,4,1]] ;
  false.
  

• La solución es

  	Nacionalidad	Color	Profesión	Animal	Bebida
  1	Noruego	Amarilla	Diplomático	Zorro	Agua
  2	Italiano	Azul	Doctor	Caballo	Te
  3	Inglés	Roja	Escultor	Caracol	Leche
  4	Espagnol	Blanca	Violinista	Perro	Zumo
  5	Japones	Verde	Pintor	Cebra	Cafe

• El código del problema de la cebra se encuentra en cebra.pl.

• El módulo de restricciones booleanas se importa con

:- use_module(library(clpb)).  

• Los valores de verdad son
  • 0 (falso) y
  • 1 (verdadero).
• Las conectivas lógicas son
  • ~ (negación),
  • + (disyunción) y
  • * (conjunción).
• Las relaciones entre expresiones lógicas son
  • =:= (igualdad que corresponde a la equivalencia),
  • =\= (desigualdad),
  • =< (menor o igual que corresponde a la implicación),
  • >= (mayor o igual),
  • < (menor) y
  • > (mayor).

• sat(E) se verifica si la expresión E es satisfacible. Por ejemplo.

  ?- sat(X*Y).
  X = Y, Y = 1.
  
  ?- sat(X * ~X).
  false.
  
  ?- sat(X+Y), labeling([X,Y]).
  X = 0, Y = 1 ;
  X = 1, Y = 0 ;
  X = Y, Y = 1.
  
  ?- sat(X*Y + X*Z), labeling([X,Y,Z]).
  X = Z, Z = 1, Y = 0 ;
  X = Y, Y = 1, Z = 0 ;
  X = Y, Y = Z, Z = 1.
  

• taut(E, T) se verifica que

  • T = 1, si E es una tautología,
  • T = 0, si E es un insatisfacible,
  • falla, en caso contrario.

  Por ejemplo,

  ?- taut(X + ~X,T).
  T = 1,
  sat(X=:=X).
  
  ?- taut(X * ~X,T).
  T = 0,
  sat(X=:=X).
  
  ?- taut(X,T).
  false.
  
  ?- sat(X =< Y), sat(Y =< Z), taut(X =< Z, T).
  T = 1,
  sat(X=:=X*Y),
  sat(Y=:=Y*Z).
  

• La expresión X^E significa que exista algún valor de X para el que se verifica la expresión E. Por ejemplo,

  ?- sat(X^(X*Y)).
  Y = 1,
  sat(X=:=X).
  
  ?- sat(X^(X*(~X))).
  false.
  
  ?- sat(X^Y^(X+Y)).
  sat(X=:=X),
  sat(Y=:=Y).
  

• card(Ns,Es) se verifica si el número de expresiones de Es que son verdaderas pertenece a la lista de números enteros Ns. Por ejemplo,

  ?- sat(card([1],[X,Y])), labeling([X,Y]).
  X = 0,
  Y = 1 ;
  X = 1,
  Y = 0.
  
  ?- sat(card([2],[X,Y])), labeling([X,Y]).
  X = Y, Y = 1.
  
  ?- sat(card([0,2],[X,Y])), labeling([X,Y]).
  X = Y, Y = 0 ;
  X = Y, Y = 1.
  

• El manual de la librería de restricciones booleanas está en este enlace.

• El enunciado del problema de la frase correcta es: "¿Cuál de las siguientes frases es la correcta?
  1. Todas las siguientes.
  2. Ninguna de las siguientes.
  3. Todas las anteriores.
  4. Alguna de las anteriores.
  5. Ninguna de las anteriores.
  6. Ninguna de las anteriores."

• solución([A1,A2,A3,A4,A5,A6]) se verifica si Ai = 1 si la frase i del problema es correcta y Ai = 0 si la frase i del problema es incorrecta.

  :- use_module(library(clpb)).
  
  solución([A1,A2,A3,A4,A5,A6]) :-
     sat(A1 =:= A2*A3*A4*A5*A6),
     sat(A2 =:= ~(A2+A3+A4+A5+A6)),
     sat(A3 =:= A1*A2),
     sat(A4 =:= card([1,2,3],[A1,A2,A3])),
     sat(A5 =:= ~(A1+A2+A3+A4)),
     sat(A6 =:= ~(A1+A2+A3+A4+A5)).
  

• Cálculo de la solución

  ?- solución(L).
  L = [0, 0, 0, 0, 1, 0].
  

  Por tanto, la verdadera es la 5ª.

• El código del problema de la frase correcta se encuentra en La_frase_correcta.pl.

Ejercicio 1.1. Definir en CLP(R) la relación producto(V1,V2,P) que se verifica si P es el producto escalar del vector V1 por el ~V24. Por ejemplo,

?- producto([4,2],[3,7],P).
P = 26.0 
?- producto([4,2,5],[3,7,2],P).
P = 36.0 

Solución

producto([],[],0).
producto([X1|L1],[X2|L2],Z) :-
   producto(L1,L2,Y),
   {Z = X1*X2+Y}.

Ejercicio 1.2. Determinar X tal que el producto de [4,2] por [X,7] es 26.

Solución

?- producto([4,2],[X,7],26).
X = 3.0 ;
false.

Ejercicio 1.3. Determinar X e Y tales que el producto de [4,2] por [X,Y] es 26.

Solución

?- producto([4,2],[X,Y],26).
{X=6.5-0.5*Y,_13736=2.0*Y}.

Ejercicio 1.4. Resolver el sistema de ecuaciones

3*X + Y   =  5
  X + 8*Y = 17

Solución

?- producto([3,1],[X,Y],5), producto([1,8],[X,Y],17).
X = 0.9999999999999999,
Y = 2.0.

Ejercicio 2.1. Una matriz está equilibrada si cada elemento interior (es decir, que pertenece a una línea distinta de la primera y última fila y columna) es la media de sus cuatro vecinos.

Definir en CLP(R) la relación equilibrada(M)4 que se verifica si ~M es una matriz equilibrada. Por ejemplo,

?- equilibrada([[4,4,4],[0,Y,0],[0,0,0]]).
Y = 1.0 ;
false.

?- equilibrada([[4,4,4],[X,Y,0],[0,0,0]]).
{Y=1.0+0.25*X} ;
false.

?- equilibrada([[4,4,4],[X,1,Z],[0,0,0]]).
{Z= -X} ;
false.

Solución

equilibrada([_, _]).
equilibrada([R1, R2, R3 | Rs]) :- 
   equilibrada_aux(R1, R2, R3), 
   equilibrada([R2, R3 | Rs]).

equilibrada_aux([_, _], [_, _], [_, _]).
equilibrada_aux([_TL, T, TR | Ts], [ML, M, MR | Ms], [_BL, B, BR | Bs]) :-
   {4*M = T + ML + MR + B}, 
   equilibrada_aux([T, TR | Ts], [M, MR | Ms], [B, BR | Bs]). 

Ejercicio 2.2. Determinar los valores interiores de la siguiente matriz para que sea equilibrada

[[0,100,100,100,100,100, 0],
 [0,  _,  _,  _,  _,  _, 0],
 [0,  _,  _,  _,  _,  _, 0],
 [0,  _,  _,  _,  _,  _, 0],
 [0,  _,  _,  _,  _,  _, 0],
 [0,  0,  0,  0,  0,  0, 0]],

Solución

?- P = [[0,100,100,100,100,100, 0],
        [0,  _,  _,  _,  _,  _, 0],
        [0,  _,  _,  _,  _,  _, 0],
        [0,  _,  _,  _,  _,  _, 0],
        [0,  _,  _,  _,  _,  _, 0],
        [0,  0,  0,  0,  0,  0, 0]], 
   equilibrada(P).

P = [[0, 100,      100,      100,      100,      100,       0],
     [0,  46.6117,  62.4778,  66.4292,  62.4778,  46.6117,  0],
     [0,  23.9691,  36.8702,  40.7612,  36.8702,  23.9691,  0],
     [0,  12.3945,  20.2727,  22.8752,  20.2727,  12.3945,  0],
     [0,  5.33633,  8.9508,   10.1942,   8.9508,   5.33633, 0],
     [0,  0,        0,         0,        0,        0,       0]] ;
false.

Nota: En los siguientes ejercicio se usará CLP(R) que se importa con

:- use_module(library(clpfd)).

Ejercicio 3. Definir en CLP(FD) la relación solución tal que solución([C,U,A,T,R,O],[V,E,I,N,T,E]) se verifica si el valor de cada letra es un dígito distinto y se cumple la ecuación

CUATRO * 5 = VEINTE

Solución

solución([C,U,A,T,R,O],[V,E,I,N,T,E]) :-
   Vars = [C,U,A,T,R,O,V,E,I,N],
   Vars ins 0..9,                                 % Los valores son los dígitos
   all_distinct(Vars),                            % Los valores son distintos
      (100000*C+10000*U+1000*A+100*T+10*R+O) * 5
   #=  100000*V+10000*E+1000*I+100*N+10*T+E,
   label(Vars).

Cálculo de la solución

?- solución([C,U,A,T,R,O],[V,E,I,N,T,E]).
C = 1,
U = 7,
A = 0,
T = 4,
R = 6,
O = 9,
V = 8,
E = 5,
I = 2,
N = 3 ;
false.

?- solución(L1, L2).
L1 = [1,7,0,4,6,9],
L2 = [8,5,2,3,4,5] ;
false.

Ejercicio 4.1. Un contrabandista tiene una mochila de capacidad limitada, supongamos que a 9 unidades de peso. Él puede hacer contrabando de botellas de whisky de 4 unidades de peso, botes de colonia de 3 unidades de peso y cartones de tabaco de 2 unidades de peso. Las ganancias en las botellas de whisky, botes de colonia y cartones de tabaco son de 15, 10 y 7 euros, respectivamente.

Definir en CLP(FD) la relación viaje_rentable(+N,?W,?C,?T,?G) que se verifique si con W unidades de whisky, C de colonia y T de tabacos se obtiene una ganancia G que es mayor o igual que N. Por ejemplo,

?- viaje_rentable(30, W, C, T, G).
W = 0,
C = 1,
T = 3,
G = 31 ;
W = T, T = 0,
C = 3,
G = 30 ;
W = C, C = T, T = 1,
G = 32 ;
W = 2,
C = T, T = 0,
G = 30.

Solución

viaje_rentable(N,W,C,T,G) :-
   [W,C,T] ins 0..9, 
   4*W + 3*C + 2*T #=< 9, 
   G #= 15*W + 10*C + 7*T,
   G #>= N,
   label([W,C,T]).

Ejercicio 4.2. Definir en CLP(FD) la relación viaje_óptimo(?W,?C,?T) que se verifique si con W unidades de whisky, C de colonia y T de tabacos se obtiene la máxima ganancia. Por ejemplo,

?- viaje_óptimo(W,C,T).
W = C, C = T, T = 1 ;
false.

Solución

viaje_óptimo(W,C,T) :-
   viaje_rentable(_,W,C,T,G),
   not((viaje_rentable(_,_,_,_,G1), G1 #> G)).

Ejercicio 5. Se tiene que realizar simultáneamente 4 tareas y se dispone de cuatro empresas que han realizado un presupuesto para cada tarea resumido en la siguiente tabla

   T1 T2 T3 T4
E1 3  9  7  6
E2 2  8  5  9
E3 6  7  3  8
E4 7  9  4  7

Definir en CLP(FD) la relación asignación_óptima(M,L) que se verifica si L es la asignación de las tareas que hace mínimo el coste total. Por ejemplo,

?- asignación_óptima([[3,9,7,6],
                      [2,8,5,9],
                      [6,7,3,8],
                      [7,9,4,7]],
                     [T1,T2,T3,T4]).
T1 = 3
T2 = 4
T3 = 1
T4 = 2

Solución

asignación([E1,E2,E3,E4],[T1,T2,T3,T4],C) :-
   L = [T1,T2,T3,T4],
   L ins 1..4,           % Ti=j significa que el trabajo i se asigna a j
   all_distinct(L),
   nth1(T1,E1,CT1),
   nth1(T2,E2,CT2),
   nth1(T3,E3,CT3),
   nth1(T4,E4,CT4),
   C #= CT1+CT2+CT3+CT4,
   label(L).

asignación_óptima([E1,E2,E3,E4],[T1,T2,T3,T4]) :-
   asignación([E1,E2,E3,E4],[T1,T2,T3,T4],C),
   not((asignación([E1,E2,E3,E4],[_,_,_,_],C1), C1 > C)).

Nota. Es los siguientes ejercicios se definirán relaciones estudiadas en temas % anteriores pero usando restricciones sobre dominios finitos.

Ejercicio 6. Definir la relación factorial(X,Y) se verifica si Y es el factorial de X. Por ejemplo,

?- factorial(3,Y).
Y = 6 ;
false.

?- factorial(X,6).
X = 3 ;
false.

?- factorial(X,7).
false.

Solución

factorial(0,1).
factorial(X,Y) :-
   X #> 0,
   A #= X - 1,
   Y #= X * B,
   factorial(A,B).

Ejercicio 7. Definir la relación máximo(X,Y,Z) que se verifica si Z es el máximo de los números X e Y. Por ejemplo,

?- máximo(2,3,Z).
Z = 3.

?- máximo(2,Y,3).
Y = 3.

?- máximo(X,3,3).
X in inf..3.

Solución

máximo(X,Y,Z) :-
   Z #= max(X,Y).

Ejercicio 8. Dados dos enteros positivos X e Y, el máximo común divisor (mcd) D puede obtenerse de la siguiente manera:

• Si X e Y son iguales, entonces D es igual a X.
• Si X < Y, entonces D es igual al máximo común divisor de X y la diferencia ~Y-X4.
• Si Y < X entonces D es igual al máximo común divisor de X y la diferencia X-Y.

Definir el predicado mcd(X,Y,D) que se verifica si D es el máximo común divisor de los enteros positivos X e Y. Por ejemplo,

?- mcd(6,10,D).
D = 2 

Solución

mcd(X,X,X).
mcd(X,Y,Z) :-
   X  #< Y,
   Y1 #= Y - X,
   mcd(X,Y1,Z).
mcd(X,Y,Z) :-
   X #> Y,
   mcd(Y,X,Z).

Ejercicio 9.1. Supongamos que los cuadros del tablero de ajedrez los representamos por pares de números [X,Y] con X e Y entre 1 y 8.

Definir la relación salta(C1,C2) que se verifica si el caballo puede pasar en un movimiento del cuadrado C1 al cuadrado C2. Por ejemplo,

?- salta([1,1],S).
S = [3,2] ;
S = [2,3] ;
false.

?- salta(X,[3,2]).
X = [1,1] ;
X = [1,3] ;
X = [5,1] ;
X = [5,3] ;
X = [2,0] ;
X = [2,4] ;
X = [4,0] ;
X = [4,4].

Solución

salta([X,Y],[X1,Y1]) :-
   [X,Y,X1,Y1] ins 1..8,
   dxy(Dx,Dy),
   X1 #= X+Dx,
   Y1 #= Y+Dy.

% dxy(?X,?Y) se verifica si un caballo puede moverse X espacios
% horizontales e Y verticales.
dxy(2,1).
dxy(2,-1).
dxy(-2,1).
dxy(-2,-1).
dxy(1,2).
dxy(1,-2).
dxy(-1,2).
dxy(-1,-2).

Ejercicio 9.2. Definir la relación camino(L) que se verifica si L es una lista de cuadrados representando el camino recorrido por un caballo sobre un tablero vacío. Por ejemplo,

?- camino([[1,1]|C]).
C = [] ;
C = [[3,2]] ;
C = [[3,2],[5,3]] ;
C = [[3,2],[5,3],[7,4]] 

?- camino(L), append(_L1,[[5,3]],L).
L = [[5,3]] ;
L = [[3,2],[5,3]] ;
L = [[3,4],[5,3]] ;
L = [[7,2],[5,3]] ;
L = [[7,4],[5,3]]

?- camino(L), length(L,4), append(_L1,[[5,3]],L).
L = [[2,3],[1,1],[3,2],[5,3]] ;
L = [[3,4],[1,3],[3,2],[5,3]] 

Solución

camino([_]).
camino([C1,C2|L]) :-
   camino([C2|L]),
   salta(C1,C2),
   \+ member(C1,L),
   \+ member(C2,L).

Ejercicio 10. Definir la relación factores(X,Y,Z) que se verifica si el producto de X e Y es Z. Por ejemplo,

?- factores(2,3,Z).
Z = 6.

?- factores(2,Y,6).
Y = 3.

?- factores(X,3,6).
X = 2.

?- factores(2,Y,7).
false.

?- factores(X,Y,6).
X = -6,
Y = -1 ;
X = -3,
Y = -2 ;
X = -2,
Y = -3 ;
X = -1,
Y = -6 ;
X = 1,
Y = 6 ;
X = 2,
Y = 3 ;
X = 3,
Y = 2 ;
X = 6,
Y = 1.

Solución

factores(X,Y,Z) :-
   Z #= X * Y,
   label([X,Y]).

Ejercicio 11. Definir la relación suma_segura(X,Y,Z) se verifica si X e Y son enteros y Z es la suma de X e Y. Por ejemplo,

?- suma_segura(2,3,Z).
Z = 5.

?- suma_segura(2,Y,5).
Y = 3.

?- suma_segura(X,3,5).
X = 2.

?- suma_segura(X,Y,3).
X = 0,
Y = 3 ;
X = 1,
Y = 2 ;
X = 2,
Y = 1 ;
X = 3,
Y = 0.

Solución

suma_segura(X,Y,Z) :-
   [X,Y] ins 0..sup,
   Z #= X+Y,
   label([X,Y]).

Ejercicio 12. El problema de los cuadrados mágicos consiste en colocar los números 1, 2, 3, 4, 5, 6, 7, 8 y 9 en un cuadrado 3x3 de forma que todas las líneas (filas, columnas y diagonales) sumen igual; es decir, buscar los valores para las variables A, B ,C, D, E, F, G, H, I.

tales que {A,B,C,D,E,F,G,H,I} = {1,2,3,4,5,6,7,8,9}, A+B+C = 15, D+E+F = 15, G+H+I = 15, A+D+G = 15, B+E+H = 15, C+F+I = 15, A+E+I = 15, C+E+G = 15.

Definir la relación cuadrado(L) que se verifica si L es una solución del problema de los cuadrados mágicos. Por ejemplo,

?- cuadrado(L).
L = [2,7,6,9,5,1,4,3,8] ;
L = [2,9,4,7,5,3,6,1,8] 
?- findall(_X,cuadrado(_X),_L),length(_L,N).
N = 8.

1ª solución

cuadrado([A,B,C,D,E,F,G,H,I]) :-
   [A,B,C,D,E,F,G,H,I] ins 1..9,
   all_distinct([A,B,C,D,E,F,G,H,I]),
   A+B+C #= 15,
   D+E+F #= 15,
   G+H+I #= 15,
   A+D+G #= 15,
   B+E+H #= 15,
   C+F+I #= 15,
   A+E+I #= 15,
   C+E+G #= 15,
   label([A,B,C,D,E,F,G,H,I]).

2ª solución

cuadrado_2(Sol):-
  Sol = [A,B,C,D,E,F,G,H,I],
  Sol ins 1..9,
  all_distinct(Sol),
  maplist(#=(15),
    [A+B+C,
     D+E+F,
     G+H+I,
     A+D+G,
     B+E+H,
     C+F+I,
     A+E+I,
     C+E+G]),
  label(Sol).

Ejercicio 13, La sucesión de Fibonacci es 1, 1, 2, 3, 5, 8, … y está definida por

f(1) = 1
f(2) = 1
f(n) = f(n-1)+f(n-2), si n > 2

Definir la relación fibonacci(N,X) que se verifica si X es el N-ésimo término de la sucesión de Fibonacci. Por ejemplo,

?- fibonacci(6,X).
X = 8 

?- fibonacci(X,8).
X = 6 

?- fibonacci(X,9).
false.

Solución

fibonacci(1,1).
fibonacci(2,1).
fibonacci(N,F) :-
   N #> 2,
   F #>= 2,
   N1 #= N-1,
   N2 #= N-2,
   F #= F1 + F2,
   [F1,F2] ins 1..sup,
   fibonacci(N1,F1),
   fibonacci(N2,F2).

Ejercicio 14. El problema de las N reinas consiste en colocar N reinas en un tablero rectangular de dimensiones N por N de forma que no se encuentren más de una en la misma línea: horizontal, vertical o diagonal.

Definir la relación reinas(N,S) que se verifica si S es una solución del problema de las N reinas. Por ejemplo,

?- reinas(4, Rs).
Rs = [2,4,1,3] ;
Rs = [3,1,4,2] 

?- reinas(8, Rs).
Rs = [1,5,8,6,3,7,2,4]

?- findall(S,reinas(8,S),_L), length(_L,N).
N = 92.

Solución

reinas(N, Rs) :-
   length(Rs, N),
   Rs ins 1..N,
   seguras(Rs),
   label(Rs).

seguras([]).
seguras([R|Rs]) :-
   seguras(Rs, R, 1),
   seguras(Rs).

seguras([], _, _).
seguras([R|Rs], R0, D0) :-
   R0 #\= R,
   abs(R0 - R) #\= D0,
   D1 #= D0 + 1,
   seguras(Rs, R0, D1).

Ejercicio 15.1. Se considera el siguiente mapa

+----------+----------+  
|    a     |     b    |  
+----+-----+-----+----+  
|    |           |    |  
| c  |     d     | e  |  
|    |           |    |  
+----+-----+-----+----+  
|    f     |     g    |  
+----------+----------+  

Definir la relación coloración1(Rs) que se verifica si Rs es una de números que representa los colores de los regiones de Rs tal que las regiones vecinas tengan colores distintos. Por ejemplo,

?- coloración1(Rs).
Rs = [1,2,2,3,1,1,2] ;
Rs = [1,2,2,3,1,1,4] 

Solución

coloración1(Rs) :-
   Rs = [A,B,C,D,E,F,G],
   distinta(A,[B,C,D]),
   distinta(B,[A,D,E]),
   distinta(C,[A,D,F]),
   distinta(D,[A,B,C,E,F,G]),
   distinta(E,[B,D,G]),
   distinta(F,[C,D,G]),
   distinta(G,[D,E,F]),
   label(Rs).

distinta(X,Ys) :-
   X in 1..4,
   Ys ins 1..4,
   maplist(#\=(X),Ys),
   label([X|Ys]).

Ejercicio 15.2. Se considera el siguiente mapa

+----+-----+-----+----+
| a  |  b  |  c  | d  |
+----+-----+-----+----+
| e  |           | f  |
+----+     k     +----+
| g  |           | h  |
+----+-----+-----+----+
|    i     |     j    |
+----------+----------+

Definir la relación coloración2(Rs) que se verifica si Rs es una de números que representa los colores de los regiones de Rs tal que las regiones vecinas tengan colores distintos. Por ejemplo,

?- coloración2(Rs).
Rs = [1,2,1,2,3,3,1,1,2,3,4] ;
Rs = [1,2,1,2,3,3,1,1,3,2,4] 

Solución

coloración2(Rs) :-
   Rs = [A,B,C,D,E,F,G,H,I,J,K],
   distinta(A,[B,E,K]),
   distinta(B,[A,C,E,K]),
   distinta(C,[B,D,F,K]),
   distinta(D,[C,F,K]),
   distinta(E,[A,B,G,K]),
   distinta(F,[C,D,H,K]),
   distinta(G,[E,I,K]),
   distinta(H,[F,J,K]),
   distinta(I,[G,J,K]),
   distinta(J,[I,H,K]),
   distinta(K,[A,B,C,D,E,F,G,H,I,J]),
   label(Rs).

Ejercicio 16. El problema de los animales es el siguiente:

Un granjero tiene pollos y vacas. Sabiendo que tiene A animales, y los animales tienen P patas en total, ¿cuántos pollos tiene el granjero?

Definir la relación animales(A,P,X,Y) que se verifica si X es el número de pollos e Y es el número de vacas sabiendo que hay A animales que tienen P patas en total. Por ejemplo,

?- animales(30,74,Pollos,Vacas).
Pollos = 23,
Vacas = 7.

Solución

animales(A,P,Pollos,Vacas) :-
   Pollos + Vacas #= A,
   2*Pollos + 4*Vacas #= P,
   [Pollos, Vacas] ins 0..sup.

Ejercicio 17. Un árbol binario es vacío o consta de tres partes: la raíz (que debe de ser un número positivo), el subárbol izquierdo (que debe ser un árbol binario) y el subárbol derecho (que debe ser un árbol binario). Usaremos la siguiente representación

• nil representa el árbol vacío
• t(I,R,D) representa el árbol de la raíz R, subárbol izquierdo I y subárbol derecho D.

Por ejemplo, el término t(t(nil,2,nil),1,t(t(nil,4,nil),3,nil)) representa el árbol

   1                                   
 /   \                                 
2     3                                
     /                                 
    4                                  

Definir la relación máximo(+T,-X) que se verifica si X es el máximo de los nodos del árbol T. Por ejemplo,

?- máximo(nil,N).
N = 0. 
?- máximo(t(nil,2,nil),N).
N = 2. 
?- máximo(t(t(nil,2,nil),3,nil),N).
N = 3.

Solución

máximo(nil,0).
máximo(t(I,R,D),M):-
   máximo(I,MI),
   máximo(D,MD),
   M1 #= max(MI,MD),
   M #= max(R,M1).

Nota: El código con las soluciones de los ejercicios se encuentra en ejercicios-tema-9.pl.

Ejercicio 18. Definir la relación cota_superior(+L,N) que se verifique si N es una cota superior de L (es decir, todos los elementos de L son menores o iguales que N). Por ejemplo,

?- cota_superior([1,5,3],7).
true.

?- cota_superior([1,5,3],5).
true.

?- cota_superior([1,5,3],4).
false.

?- cota_superior([1,5,3],X).
X in 5..sup.

1ª solución

cota_superior_1([],_).
cota_superior_1([X|L],N) :-
   X #=< N,
   cota_superior_1(L,N).

2ª solución

cota_superior_2(L,N) :-
   max_list(L,M),
   N #>= M.