Factorial módulo
Definir la función
factorialMod :: Integer -> Integer -> Integer
tal que (factorialMod n x) es el factorial de x módulo n. Por ejemplo,
factorialMod (7+10^9) 100 == 437918130 factorialMod (7+10^9) (5*10^6) == 974067448
Recorrido por niveles de árboles binarios
Los árboles binarios con valores en las hojas y en los nodos se definen por
data Arbol a = H a | N a (Arbol a) (Arbol a) deriving (Eq, Show)
Por ejemplo, el árbol
1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9
se pueden representar por
ejArbol :: Arbol Int ejArbol = N 1 (N 2 (H 4) (N 5 (H 8) (H 9))) (N 3 (H 6) (H 7))
Definir la función
recorrido :: Arbol t -> [t]
tal que (recorrido a) es el recorrido del árbol a por niveles desde la raíz a las hojas y de izquierda a derecha. Por ejemplo,
λ> recorrido (N 1 (N 2 (H 4) (N 5 (H 8) (H 9))) (N 3 (H 6) (H 7))) [1,2,3,4,5,6,7,8,9] λ> recorrido (N 1 (N 3 (H 6) (H 7)) (N 2 (H 4) (N 5 (H 8) (H 9)))) [1,3,2,6,7,4,5,8,9] λ> recorrido (N 1 (N 3 (H 6) (H 7)) (N 2 (H 4) (H 5))) [1,3,2,6,7,4,5] λ> recorrido (N 1 (N 2 (H 4) (H 5)) (N 3 (H 6) (H 7))) [1,2,3,4,5,6,7] λ> recorrido (N 1 (N 2 (H 4) (H 5)) (H 3)) [1,2,3,4,5] λ> recorrido (N 1 (H 4) (H 3)) [1,4,3] λ> recorrido (H 3) [3]
Sucesión de raíces enteras de los números primos
Definir las siguientes funciones
raicesEnterasPrimos :: [Integer] posiciones :: Integer -> (Int,Int) frecuencia :: Integer -> Int grafica_raicesEnterasPrimos :: Int -> IO () grafica_posicionesIniciales :: Integer -> IO () grafica_frecuencias :: Integer -> IO ()
tales que
-
raicesEnterasPrimoses la sucesión de las raíces enteras (por defecto) de los números primos. Por ejemplo,
λ> take 20 raicesEnterasPrimos [1,1,2,2,3,3,4,4,4,5,5,6,6,6,6,7,7,7,8,8] λ> raicesEnterasPrimos !! 2500000 6415
-
(posiciones x)es el par formado por la menor y la mayor posición de x en la sucesión de las raíces enteras de los números primos. Por ejemplo,
posiciones 2 == (2,3) posiciones 4 == (6,8) posiciones 2017 == (287671,287931) posiciones 2018 == (287932,288208)
-
(frecuencia x)es el número de veces que aparece x en la sucesión de las raíces enteras de los números primos. Por ejemplo,
frecuencia 2 == 2 frecuencia 4 == 3 frecuencia 2017 == 261 frecuencia 2018 == 277
-
(grafica_raicesEnterasPrimos n)dibuja la gráfica de los n primeros términos de la sucesión de las raíces enteras de los números primos. Por ejemplo,(grafica_raicesEnterasPrimos 200)dibuja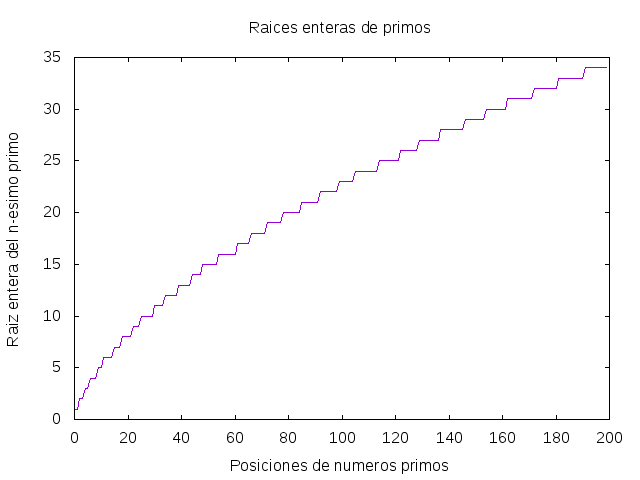
-
(grafica_posicionesIniciales n)dibuja la gráfica de las menores posiciones de los n primeros números en la sucesión de las raíces enteras de los números primos. Por ejemplo,(grafica_posicionesIniciales 200)dibuja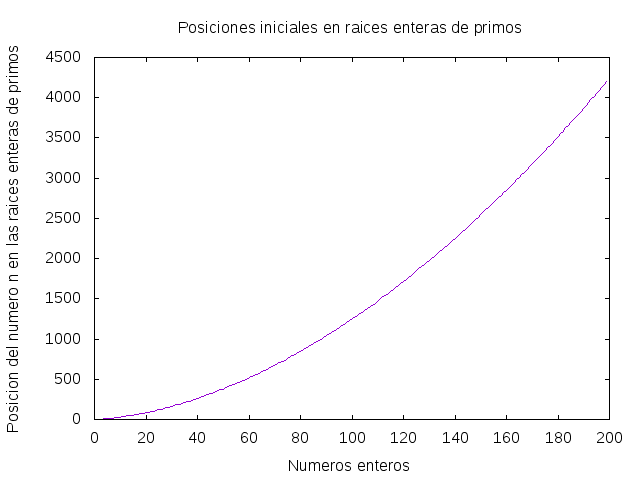
-
(grafica_frecuencia n)dibuja la gráfica de las frecuencia de los n primeros números en la sucesión de las raíces enteras de los números primos. Por ejemplo,(grafica_frecuencia 200)dibuja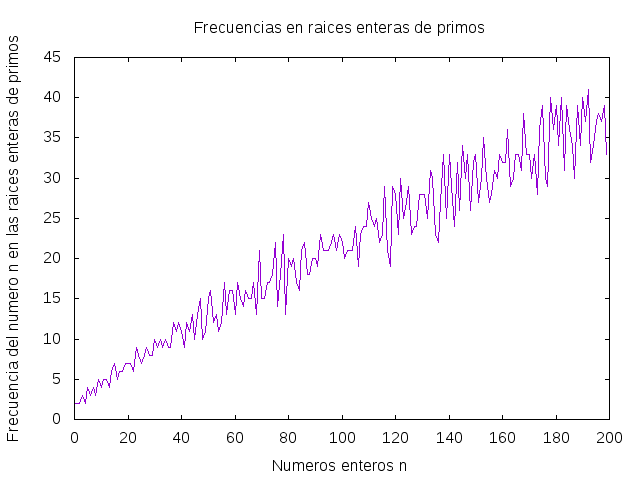
Posiciones de las mayúsculas
Definir la función
posicionesMayusculas :: String -> [Int]
tal que (posicionesMayusculas cs) es la lista de las posiciones de las mayúsculas de la cadena cs. Por ejemplo,
posicionesMayusculas "SeViLLa" == [0,2,4,5] posicionesMayusculas "aAbB" == [1,3] posicionesMayusculas "ABCDEF" == [0,1,2,3,4,5] posicionesMayusculas "4ysdf4" == [] posicionesMayusculas "" == []
Rotaciones divisibles por 8
Las rotaciones de 928160 son 928160, 281609, 816092, 160928, 609281 y 92816 de las que 3 son divisibles por 8 (928160, 160928 y 92816).
Definir la función
nRotacionesDivisiblesPor8 :: Integer -> Int
tal que (nRotacionesDivisiblesPor8 x) es el número de rotaciones de x divisibles por 8. Por ejemplo,
nRotacionesDivisiblesPor8 928160 == 3 nRotacionesDivisiblesPor8 43262488612 == 4 nRotacionesDivisiblesPor8 (read (take (10^4) (cycle "248"))) == 6666
Sumable sin vecinos
En la lista [3,2,5,7,4] el número 12 se puede escribir como una suma de elementos de la lista sin incluir sus vecinos (ya que es la suma de 3, 5 y 4); en cambio, 14 no lo es (porque es la suma de 3, 7 y 4, pero 7 y 4 son vecinos).
Definir la función
esSumableSinVecinos :: [Int] -> Int -> Bool
tal que (esSumableSinVecinos xs n) se verifica si n se puede escribir como una suma de elementos de xs que no incluye a ninguno de sus vecinos. Por ejemplo,
esSumableSinVecinos [3,2,5,7,4] 12 == True esSumableSinVecinos [3,2,5,7,4] 9 == True esSumableSinVecinos [3,2,5,7,4] 6 == True esSumableSinVecinos [3,2,5,7,4] 14 == False esSumableSinVecinos [3,2,5,7,4] 1 == False
Suma de las hojas de mínimo nivel
Los árboles binarios con valores en las hojas y en los nodos se definen por
data Arbol a = H a | N a (Arbol a) (Arbol a) deriving (Eq, Show)
Por ejemplo, el árbol
1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9
se pueden representar por
ejArbol :: Arbol Int ejArbol = N 1 (N 2 (H 4) (N 5 (H 8) (H 9))) (N 3 (H 6) (H 7))
En el árbol anterior, los valores de las hojas de menor nivel son 4, 6 y 7 cuya suma es 17.
Definir la función
suma :: Num t => Arbol t -> t
tal que (suma a) es la suma de los valores de las hojas de menor nivel del árbol a. Por ejemplo,
suma ejArbol == 17 suma (N 1 (N 2 (H 4) (H 5)) (N 3 (H 6) (H 7))) == 22 suma (N 1 (H 2) (N 3 (H 6) (H 7))) == 2 suma (N 1 (H 2) (H 3)) == 5 suma (H 2) == 2
Vecino en lista circular
En la lista circular [3,2,5,7,9]
- el vecino izquierdo de 5 es 2 y su vecino derecho es 7,
- el vecino izquierdo de 9 es 7 y su vecino derecho es 3,
- el vecino izquierdo de 3 es 9 y su vecino derecho es 2,
- el elemento 4 no tiene vecinos (porque no está en la lista).
Para indicar las direcciones se define el tipo de datos
data Direccion = I | D deriving Eq
Definir la función
vecino :: Eq a => Direccion -> [a] -> a -> Maybe a
tal que (vecino d xs x) es el vecino de x en la lista de elementos distintos xs según la dirección d. Por ejemplo,
vecino I [3,2,5,7,9] 5 == Just 2 vecino D [3,2,5,7,9] 5 == Just 7 vecino I [3,2,5,7,9] 9 == Just 7 vecino D [3,2,5,7,9] 9 == Just 3 vecino I [3,2,5,7,9] 3 == Just 9 vecino D [3,2,5,7,9] 3 == Just 2 vecino I [3,2,5,7,9] 4 == Nothing vecino D [3,2,5,7,9] 4 == Nothing
Cadenas opuestas
La opuesta de una cadena de letras es la cadena obtenida cambiando las minúsculas por mayúsculas y las minúsculas por mayúsculas. Por ejemplo, la opuesta de "SeViLLa" es "sEvIllA".
Definir la función
esOpuesta :: String -> String -> Bool
tal que (esOpuesta s1 s2) se verifica si las cadenas de letras s1 y s2 son opuestas. Por ejemplo,
esOpuesta "ab" "AB" `== True esOpuesta "aB" "Ab" `== True esOpuesta "aBcd" "AbCD" `== True esOpuesta "aBcde" "AbCD" `== False esOpuesta "AB" "Ab" `== False esOpuesta "" "" `== True
Menor con suma de dígitos dada
Definir la función
minSumDig :: Integer -> Integer
tal que (minSumDig n) es el menor número x tal que la suma de los dígitos de x es n. Por ejemplo,
minSumDig 1 == 1 minSumDig 12 == 39 minSumDig 21 == 399 (length . show . minSumDig) (3*10^5) == 33334 (length . show . minSumDig) (3*10^6) == 333334 (length . show . minSumDig) (3*10^7) == 3333334 (length . show . minSumDig) (4*10^7) == 4444445 (length . show . minSumDig) (5*10^7) == 5555556