Ir al contenido principal

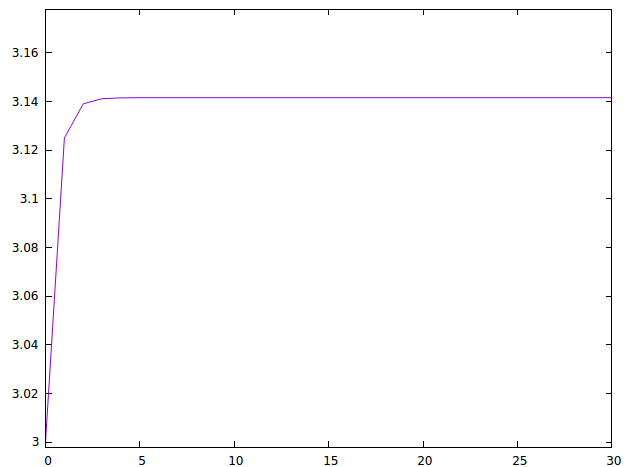
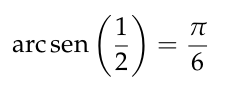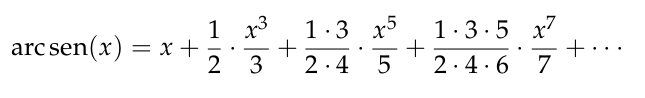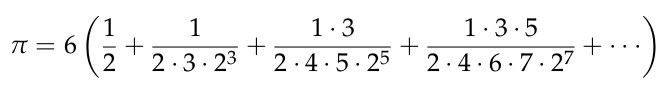Número de islas rectangulares de una matrizexer

Misceláneas

En este problema se consideran matrices cuyos elementos son 0 y 1. Los valores 1 aparecen en forma de islas rectangulares separadas por 0 de forma que como máximo las islas son diagonalmente adyacentes. Por ejemplo,

ej1, ej2 :: Array (Int,Int) Int
ej1 = listArray ((1,1),(6,3))
                [0,0,0,
                 1,1,0,
                 1,1,0,
                 0,0,1,
                 0,0,1,
                 1,1,0]
ej2 = listArray ((1,1),(6,6))
                [1,0,0,0,0,0,
                 1,0,1,1,1,1,
                 0,0,0,0,0,0,
                 1,1,1,0,1,1,
                 1,1,1,0,1,1,
                 0,0,0,0,1,1]

Definir la función

numeroDeIslas :: Array (Int,Int) Int -> Int

tal que (numeroDeIslas p) es el número de islas de la matriz p. Por ejemplo,

numeroDeIslas ej1  ==  3
numeroDeIslas ej2  ==  4

Leer más…

La codificación de Luka

Misceláneas

En el problema Kemija se utiliza la codificación de Luka consistente en añadir detrás de cada vocal la letra 'p' seguida de la vocal. Por ejemplo, la palabra "elena" se codifica como "epelepenapa" y "luisa" por "lupuipisapa".

Definir las funciones

codifica   :: String -> String
decodifica :: String -> String

tales que + (codifica cs) es la codificación de Luka de la cadena cs. Por ejemplo,

λ> codifica "elena admira a luisa"
"epelepenapa apadmipirapa apa lupuipisapa"
λ> codifica "todo para nada"
"topodopo paparapa napadapa"
  • (decodifica cs) es la decodificación de Luka de la cadena cs. Por ejemplo,
λ> decodifica "epelepenapa apadmipirapa apa lupuipisapa"
"elena admira a luisa"
λ> decodifica "topodopo paparapa napadapa"
"todo para nada"

Leer más…

Números binarios invertidos

Misceláneas

La representación binaria de 13 es 1101, que al invertirlo da 1011 cuya representación decimal es el número 11.

Definir la función

transformado :: Integer -> Integer

tal que (transformado x) es la representación decimal del número obtenido invirtiendo la representación binaria de x. Por ejemplo,

transformado 13  ==  11
transformado 47  ==  61

Nota: El ejercicio está basado en el problema Reversed Binary Numbers de Kattis.

Leer más…

Números construibles como sumas de dos dados

Misceláneas

Un número x es construible a partir de a y b si se puede escribir como una suma cuyos sumandos son a o b (donde se supone que a y be son números enteros mayores que 0). Por ejemplo, 7 y 9 son construibles a partir de 2 y 3 ya que 7 = 2+2+3 y 9 = 3+3+3.

Definir las funciones

construibles  :: Integer -> Integer -> [Integer]
esConstruible :: Integer -> Integer -> Integer -> Bool

tales que

  • (construibles a b) es la lista de los números construibles a partir de a y b. Por ejemplo,
take 5 (construibles 2 9)  ==  [2,4,6,8,9]
take 5 (construibles 6 4)  ==  [4,6,8,10,12]
take 5 (construibles 9 7)  ==  [7,9,14,16,18]
  • (esConstruible a b x) se verifica si x es construible a partir de a y b. Por ejemplo,
esConstruible 2 3 7   ==  True
esConstruible 9 7 15  ==  False

Leer más…

Contando en la arena

Misceláneas

El problema de ayer de ¡Acepta el reto! fue Contando en la arena cuyo enunciado reproduzco a continuación:

Es ampliamente conocido que escribimos los números utilizando base 10, en la que expresamos las cantidades utilizando 10 dígitos distintos (0…9). El valor de cada uno de ellos depende de la posición que ocupe dentro del número, pues cada dígito se multiplica por una potencia de 10 distinta según cuál sea esa posición. La descomposición, por ejemplo, del número 1.234 es: 1.234 = 1×10^3 + 2×10^2 + 3×10^1 + 4×10^0 Otra base muy conocida es la base 2 al ser la utilizada por los dispositivos electrónicos. En ella sólo hay dos dígitos distintos (0 y 1), que se ven multiplicados por potencias de 2. Mucho antes de que llegaran la base 2, la base 10 e incluso los números romanos, los primeros seres humanos contaban haciendo surcos en la arena, muescas en un trozo de madera o colocando palos en línea. Estaban, sin saberlo, usando base 1. En ella sólo hay un símbolo y cada dígito es multiplicado por una potencia de 1. Dado que 1^n = 1 el resultado es que todos los dígitos tienen el mismo peso.

Definir la función

transformaAbase1 :: FilePath -> FilePath -> IO ()

tal que al evaluar (transformaAbase1 f1 f2) lee el contenido del fichero f1 (que estará compuesto por distintos números mayores que 0, cada uno en una línea) y escribe en el fichero f2 una línea con la representación en base 1 de cada uno de los números de f1 excepto el 0 final. Por ejemplo, si el contenido de "Entrada.txt" es

1
4
6
0

al evaluar (transformaAbase1 "Entrada.txt" "Salida.txt") el contenido de "Salida.txt" debe de ser

1
1111
111111

Leer más…

Cálculo de pi mediante la serie de Nilakantha

Misceláneas

Una serie infinita para el cálculo de pi, publicada por Nilakantha en el siglo XV, es \[\pi = 3 + \frac{4}{2 \cdot 3 \cdot 4} - \frac{4}{4 \cdot 5 \cdot 6} + \frac{4}{6 \cdot 7 \cdot 8} - \frac{4}{8 \cdot 9 \cdot 10} + \cdots\]

Definir las funciones

aproximacionPi :: Int -> Double
tabla          :: FilePath -> [Int] -> IO ()

tales que

  • (aproximacionPi n) es la n-ésima aproximación de pi obtenido sumando los n primeros términos de la serie de Nilakantha. Por ejemplo,
aproximacionPi 0        ==  3.0
aproximacionPi 1        ==  3.1666666666666665
aproximacionPi 2        ==  3.1333333333333333
aproximacionPi 3        ==  3.145238095238095
aproximacionPi 4        ==  3.1396825396825396
aproximacionPi 5        ==  3.1427128427128426
aproximacionPi 10       ==  3.1414067184965018
aproximacionPi 100      ==  3.1415924109719824
aproximacionPi 1000     ==  3.141592653340544
aproximacionPi 10000    ==  3.141592653589538
aproximacionPi 100000   ==  3.1415926535897865
aproximacionPi 1000000  ==  3.141592653589787
pi                      ==  3.141592653589793
  • (tabla f ns) escribe en el fichero f las n-ésimas aproximaciones de pi, donde n toma los valores de la lista ns, junto con sus errores. Por ejemplo, al evaluar la expresión
tabla "AproximacionesPi.txt" [0,10..100]

hace que el contenido del fichero "AproximacionesPi.txt" sea

+------+----------------+----------------+
| n    | Aproximación   | Error          |
+------+----------------+----------------+
|    0 | 3.000000000000 | 0.141592653590 |
|   10 | 3.141406718497 | 0.000185935093 |
|   20 | 3.141565734659 | 0.000026918931 |
|   30 | 3.141584272675 | 0.000008380915 |
|   40 | 3.141589028941 | 0.000003624649 |
|   50 | 3.141590769850 | 0.000001883740 |
|   60 | 3.141591552546 | 0.000001101044 |
|   70 | 3.141591955265 | 0.000000698325 |
|   80 | 3.141592183260 | 0.000000470330 |
|   90 | 3.141592321886 | 0.000000331704 |
|  100 | 3.141592410972 | 0.000000242618 |
+------+----------------+----------------+

al evaluar la expresión

tabla "AproximacionesPi.txt" [0,500..5000]

hace que el contenido del fichero "AproximacionesPi.txt" sea

+------+----------------+----------------+
| n    | Aproximación   | Error          |
+------+----------------+----------------+
|    0 | 3.000000000000 | 0.141592653590 |
|  500 | 3.141592651602 | 0.000000001988 |
| 1000 | 3.141592653341 | 0.000000000249 |
| 1500 | 3.141592653516 | 0.000000000074 |
| 2000 | 3.141592653559 | 0.000000000031 |
| 2500 | 3.141592653574 | 0.000000000016 |
| 3000 | 3.141592653581 | 0.000000000009 |
| 3500 | 3.141592653584 | 0.000000000006 |
| 4000 | 3.141592653586 | 0.000000000004 |
| 4500 | 3.141592653587 | 0.000000000003 |
| 5000 | 3.141592653588 | 0.000000000002 |
+------+----------------+----------------+

Leer más…

Sucesiones alícuotas

Misceláneas

La sucesión alícuota de un número x es la sucesión cuyo primer término es x y cada otro término es la suma de los divisores propios del término anterior. Por ejemplo, la sucesión alícuota de 10 es [10,8,7,1,0,0,0] ya que

la suma de los divisores propios de 10 es 5 + 2 + 1 = 8
la suma de los divisores propios de  8 es 4 + 2 + 1 = 7
la suma de los divisores propios de  7 es 1
la suma de los divisores propios de  1 es 0

Definir la función

sucAlicuota :: Integer -> [Integer]

tal que (sucAlicuota x) es la sucesión alícuota de x. Por ejemplo,

take 6 (sucAlicuota 10)       ==  [10,8,7,1,0,0]
take 6 (sucAlicuota 95)       ==  [95,25,6,6,6,6]
take 6 (sucAlicuota 220)      ==  [220,284,220,284,220,284]
sucAlicuota 1184 !! (1+10^7)  ==  1210
sucAlicuota 276 !! 200        ==  2790456740340877466506

Leer más…

Precisión de aproximaciones de pi

Misceláneas

La precisión de una aproximación x de pi es el número de dígitos comunes entre el inicio de x y de pi. Por ejemplo, puesto que 355/113 es 3.1415929203539825 y pi es 3.141592653589793, la precisión de 355/113 es 7.

Definir las siguientes funciones

mayorPrefijoComun :: Eq a => [a] -> [a] -> [a]
precisionPi       :: Double -> Int
precisionPiCR     :: CReal -> Int

tales que

  • (mayorPrefijoComun xs ys) es el mayor prefijo común de xs e ys. Por ejemplo,
mayorPrefijoComun []      [2,3,4,5]  ==  []
mayorPrefijoComun [2,3,5] []         ==  []
mayorPrefijoComun [2,3,5] [2,3,4,5]  ==  [2,3]
mayorPrefijoComun [2,3,5] [2,5,3,4]  ==  [2]
mayorPrefijoComun [2,3,5] [5,2,3,4]  ==  []
  • (precisionPi x) es la precisión de la aproximación de pi x. Por ejemplo,
precisionPi (25/8)              ==  2
precisionPi (22/7)              ==  3
precisionPi (sqrt 2 + sqrt 3)   ==  3
precisionPi (377/120)           ==  4
precisionPi (31**(1/3))         ==  4
precisionPi (7^7/4^9)           ==  5
precisionPi (355/113)           ==  7
precisionPi ((2143/22)**(1/4))  ==  9
  • (precisionPiCR x) es la precisión de la aproximación de pi x, como números reales. Por ejemplo,
precisionPiCR (log (640320^3+744)/(sqrt 163))                        == 31
precisionPiCR (log (5280^3*(236674+30303*sqrt 61)^3+744)/(sqrt 427)) == 53

Nota: Para la definición precisionPiCR se usa la librería Data.Number.CReal que se instala con

cabal install numbers

Leer más…

Cálculo de pi mediante el método de Newton

Misceláneas

El método de Newton para el cálculo de pi se basa en la relación

Cálculo de pi mediante el método de Newton

y en el desarrollo del arco seno

Cálculo de pi mediante el método de Newton

de donde se obtiene la fórmula

Cálculo de pi mediante el método de Newton

La primeras aproximaciones son

a(0) = 6*(1/2)                               = 3.0
a(1) = 6*(1/2+1/(2*3*2^3))                   = 3.125
a(2) = 6*(1/2+1/(2*3*2^3)+(1*3)/(2*4*5*2^5)) = 3.1390625

Definir las funciones

aproximacionPi :: Int -> Double
grafica        :: [Int] -> IO ()

tales que

  • (aproximacionPi n) es la n-ésima aproximación de pi con la fórmula de Newton. Por ejemplo,
aproximacionPi 0   ==  3.0
aproximacionPi 1   ==  3.125
aproximacionPi 2   ==  3.1390625
aproximacionPi 10  ==  3.1415926468755613
aproximacionPi 21  ==  3.141592653589793
pi                 ==  3.141592653589793
  • (grafica xs) dibuja la gráfica de las k-ésimas aproximaciones de pi donde k toma los valores de la lista xs. Por ejemplo, (grafica [1..30]) dibuja

Cálculo de pi mediante el método de Newton

Leer más…

Cálculo de pi mediante los métodos de Gregory-Leibniz y de Beeler

Misceláneas

La fórmula de Gregory-Leibniz para calcular pi es

Cálculo de pi mediante los métodos de Gregory-Leibniz y de Beeler

y la de Beeler es

Cálculo de pi mediante los métodos de Gregory-Leibniz y de Beeler

Definir las funciones

aproximaPiGL     :: Int -> Double
aproximaPiBeeler :: Int -> Double
graficas         :: [Int] -> IO ()

tales que

  • (aproximaPiGL n) es la aproximación de pi con los primeros n términos de la fórmula de Gregory-Leibniz. Por ejemplo,
aproximaPiGL 1       ==  4.0
aproximaPiGL 2       ==  2.666666666666667
aproximaPiGL 3       ==  3.466666666666667
aproximaPiGL 10      ==  3.0418396189294032
aproximaPiGL 100     ==  3.1315929035585537
aproximaPiGL 1000    ==  3.140592653839794
aproximaPiGL 10000   ==  3.1414926535900345
aproximaPiGL 100000  ==  3.1415826535897198
  • (aproximaPiBeeler n) es la aproximación de pi con los primeros n términos de la fórmula de Beeler. Por ejemplo,
aproximaPiBeeler 1   ==  2.0
aproximaPiBeeler 2   ==  2.6666666666666665
aproximaPiBeeler 3   ==  2.933333333333333
aproximaPiBeeler 10  ==  3.140578169680337
aproximaPiBeeler 60  ==  3.141592653589793
pi                   ==  3.141592653589793
  • (graficas xs) dibuja la gráfica de las k-ésimas aproximaciones de pi, donde k toma los valores de la lista xs, con las fórmulas de Gregory-Leibniz y de Beeler. Por ejemplo, (graficas [1..50]) dibuja

Cálculo de pi mediante los métodos de Gregory-Leibniz y de Beeler

donde la línea morada corresponde a la aproximación de Gregory-Leibniz y la verde a la de Beeler.

Leer más…