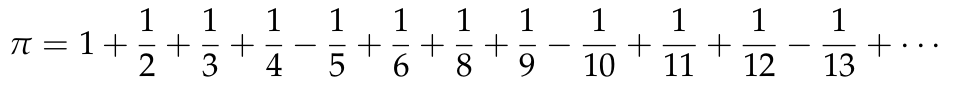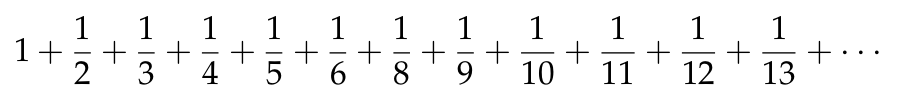Misceláneas

En 1999, L.J. Lange publicó el artículo An elegant new continued fraction for π.

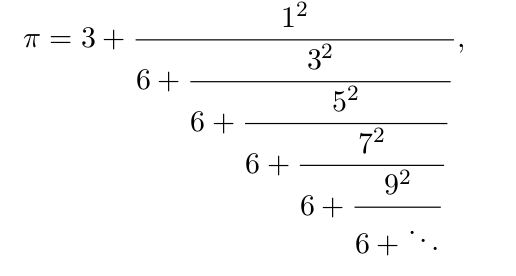
En el primer teorema del artículo se demuestra la siguiente expresión de π mediante una fracción continua $Cálculo de pi mediante la fracción continua de Lange$

La primeras aproximaciones son

a(1) = 3+1                = 4.0
a(2) = 3+(1/(6+9))        = 3.066666666666667
a(3) = 3+(1/(6+9/(6+25))) = 3.158974358974359

Definir las funciones

aproximacionPi :: Int -> Double
grafica        :: [Int] -> IO ()

tales que

(aproximacionPi n) es la n-ésima aproximación de pi con la fracción continua de Lange. Por ejemplo,

aproximacionPi 1     ==  4.0
aproximacionPi 2     ==  3.066666666666667
aproximacionPi 3     ==  3.158974358974359
aproximacionPi 10    ==  3.141287132741557
aproximacionPi 100   ==  3.141592398533554
aproximacionPi 1000  ==  3.1415926533392926

(grafica xs) dibuja la gráfica de las k-ésimas aproximaciones de pi donde k toma los valores de la lista xs. Por ejemplo, (grafica [1..10]) dibuja

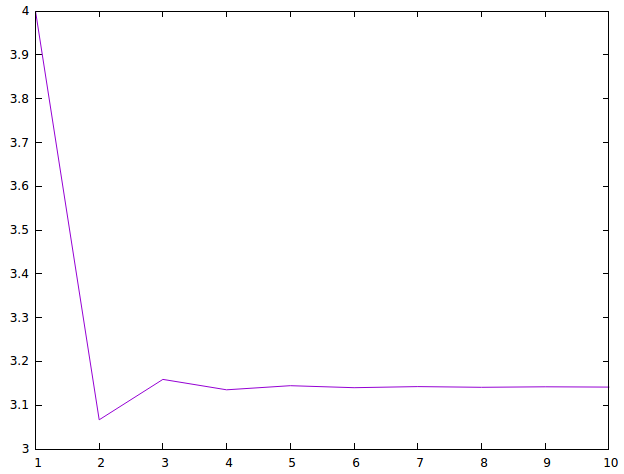
$Cálculo de pi mediante la fracción continua de Lange$

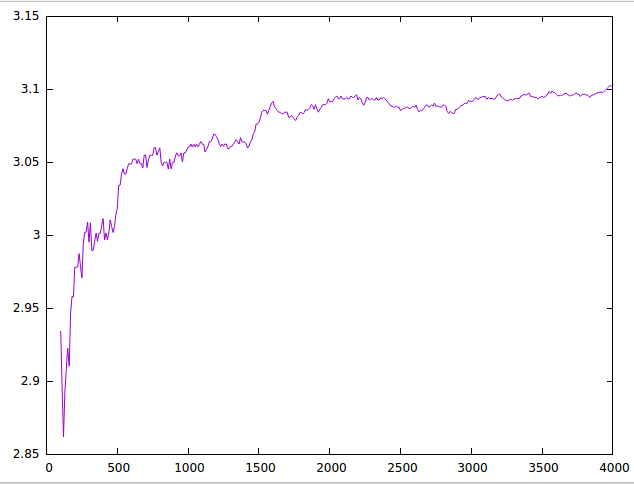
(grafica [10..100]) dibuja

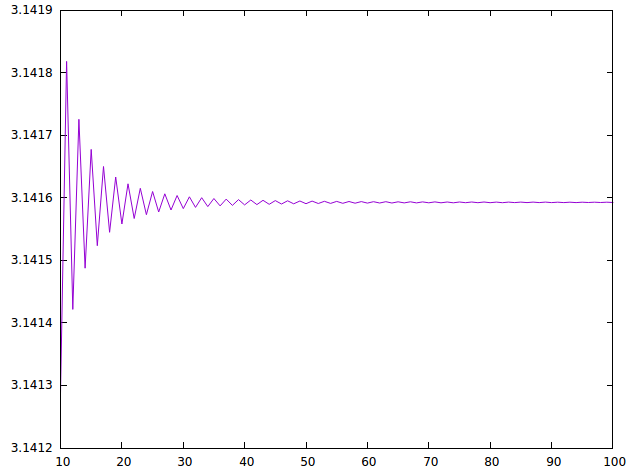
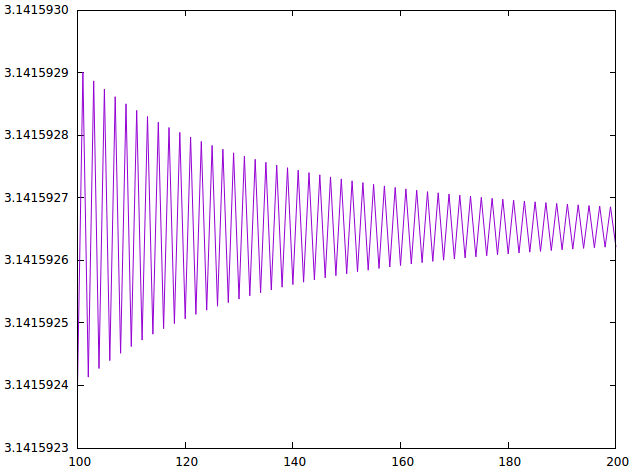
$Cálculo de pi mediante la fracción continua de Lange$

y (grafica [100..200]) dibuja

$Cálculo de pi mediante la fracción continua de Lange$

Cálculo de pi mediante la variante de Euler de la serie armónica

José A. Alonso

21-02-2017

Misceláneas

En el artículo El desarrollo más bello de Pi como suma infinita, Miguel Ángel Morales comenta el desarrollo de pi publicado por Leonhard Euler en su libro "Introductio in Analysis Infinitorum" (1748).

El desarrollo es el siguiente

Cálculo de pi mediante la variante de Euler de la serie armónica

y se obtiene a partir de la serie armónica

Cálculo de pi mediante la variante de Euler de la serie armónica

modificando sólo el signo de algunos términos según el siguiente criterio:

Dejamos un + cuando el denominador de la fracción sea un 2 o un primo de la forma 4m-1.
Cambiamos a - si el denominador de la fracción es un primo de la forma 4m+1.
Si el número es compuesto ponemos el signo que quede al multiplicar los signos correspondientes a cada factor.

Por ejemplo,

la de denominador 3 = 4x1-1 lleva un +,
la de denominador 5 = 4x1+1 lleva un -,
la de denominador 13 = 4x3+1 lleva un -,
la de denominador 6 = 2x3 lleva un + (porque los dos llevan un +),
la de denominador 10 = 2x5 lleva un - (porque el 2 lleva un + y el 5 lleva un -) y
la de denominador 50 = 5x5x2 lleva un + (un - por el primer 5, otro - por el segundo 5 y un + por el 2).

Definir las funciones

aproximacionPi :: Int -> Double
grafica        :: Int -> IO ()

tales que

(aproximacionPi n) es la aproximación de pi obtenida sumando los n primeros términos de la serie de Euler. Por ejemplo.

aproximacionPi 1        ==  1.0
aproximacionPi 10       ==  2.3289682539682537
aproximacionPi 100      ==  2.934318000847734
aproximacionPi 1000     ==  3.0603246224585128
aproximacionPi 10000    ==  3.1105295744825403
aproximacionPi 100000   ==  3.134308801935256
aproximacionPi 1000000  ==  3.1395057903490806

(grafica n) dibuja la gráfica de las aproximaciones de pi usando k sumando donde k toma los valores de la lista [100,110..n]. Por ejemplo, al evaluar (grafica 4000) se obtiene

Cálculo de pi mediante la variante de Euler de la serie armónica

Regresión lineal

José A. Alonso

20-02-2017

Misceláneas

Dadas dos listas de valores

xs = [x(1), x(2), ..., x(n)]
ys = [y(1), y(2), ..., y(n)]

la ecuación de la recta de regresión de ys sobre xs es y = a+bx, donde \[b = \frac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - \left(\sum x_i\right)^2}\] \[a = \frac{\sum y_i - b \sum x_i}{n}\]

Definir la función

regresionLineal :: [Double] -> [Double] -> (Double,Double)

tal que (regresionLineal xs ys) es el par (a,b) de los coeficientes de la recta de regresión de ys sobre xs. Por ejemplo, para los valores

ejX, ejY :: [Double]
ejX = [5,  7, 10, 12, 16, 20, 23, 27, 19, 14]
ejY = [9, 11, 15, 16, 20, 24, 27, 29, 22, 20]

se tiene

λ> regresionLineal ejX ejY
(5.195045748716805,0.9218924347243919)

Para comprobar la definición se define el procedimiento

grafica :: [Double] -> [Double] -> IO ()
grafica xs ys =
    plotPathsStyle
      [YRange (0,10+mY)]
      [(defaultStyle {plotType = Points,
                      lineSpec = CustomStyle [LineTitle "Datos",
                                              PointType 2,
                                              PointSize 2.5]},
                     zip xs ys),
       (defaultStyle {plotType = Lines,
                      lineSpec = CustomStyle [LineTitle "Ajuste",
                                              LineWidth 2]},
                     [(x,a+b*x) | x <- [0..mX]])]
    where (a,b) = regresionLineal xs ys
          mX    = maximum xs
          mY    = maximum ys

tal que (grafica xs ys) pintea los puntos correspondientes a las listas de valores xs e ys y su recta de regresión. Por ejemplo, con (grafica ejX ejY) se obtiene el siguiente dibujo

Regresión lineal

Sucesión de trazas de dígitos de pi

José A. Alonso

17-02-2017

Misceláneas

El fichero Digitos_de_pi.txt contiene el número pi con un millón de decimales; es decir,

3.1415926535897932384626433832 ... 83996346460422090106105779458151

Las matrices de orden 1x1, 2x2, ..., 5x5 formadas por los primeros dígitos de pi son

( 3 )  ( 3 1 )  ( 3 1 4 )  ( 3 1 4 1 )  ( 3 1 4 1 5 )
       ( 4 1 )  ( 1 5 9 )  ( 5 9 2 6 )  ( 9 2 6 5 3 )
                ( 2 6 5 )  ( 5 3 5 8 )  ( 5 8 9 7 9 )
                           ( 9 7 9 3 )  ( 3 2 3 8 4 )
                                        ( 6 2 6 4 3 )

y sus trazas (es decir, sumas de los elementos de la diagonal principal) son 3, 4, 13, 20 y 25, respectivamente.

Definir la función

trazas :: Int -> IO [Int]

tal que (trazas n) es la lista de las trazas de las matrices de orden 1x1, 2x2, 3x3, ..., nxn formadas por los primeros dígitos de pi. Por ejemplo,

λ> trazas 20
[3,4,13,20,25,30,19,32,41,59,62,64,58,75,62,60,80,99,78,108]
λ> ts <- trazas 1000
λ> maximum ts
4644
λ> maximum <$> trazas 1000
4644

Distribución de dígitos de pi

José A. Alonso

16-02-2017

Misceláneas

Se pueden generar los dígitos de Pi, como se explica en el artículo Unbounded spigot algorithms for the digits of pi, con la función digitosPi definida por

digitosPi :: [Integer]
digitosPi = g(1,0,1,1,3,3) where
  g (q,r,t,k,n,l) =
    if 4*q+r-t < n*t
    then n : g (10*q, 10*(r-n*t), t, k, div (10*(3*q+r)) t - 10*n, l)
    else g (q*k, (2*q+r)*l, t*l, k+1, div (q*(7*k+2)+r*l) (t*l), l+2)

Por ejemplo,

λ> take 25 digitosPi
[3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6,4,3]

La distribución de los primeros 25 dígitos de pi es [0,2,3,5,3,3,3,1,2,3] ya que el 0 no aparece, el 1 ocurre 2 veces, el 3 ocurre 3 veces, el 4 ocurre 5 veces, ...

Usando digitosPi, definir las siguientes funciones

distribucionDigitosPi :: Int -> [Int]
frecuenciaDigitosPi   :: Int -> [Double]

tales que

(distribucionDigitosPi n) es la distribución de los n primeros dígitos de pi. Por ejemplo,

λ> distribucionDigitosPi 10
[0,2,1,2,1,2,1,0,0,1]
λ> distribucionDigitosPi 100
[8,8,12,12,10,8,9,8,12,13]
λ> distribucionDigitosPi 1000
[93,116,103,103,93,97,94,95,101,105]
λ> distribucionDigitosPi 5000
[466,531,496,460,508,525,513,488,492,521]

(frecuenciaDigitosPi n) es la frecuencia de los n primeros dígitos de pi. Por ejemplo,

λ> frecuenciaDigitosPi 10
[0.0,20.0,10.0,20.0,10.0,20.0,10.0,0.0,0.0,10.0]
λ> frecuenciaDigitosPi 100
[8.0,8.0,12.0,12.0,10.0,8.0,9.0,8.0,12.0,13.0]
λ> frecuenciaDigitosPi 1000
[9.3,11.6,10.3,10.3,9.3,9.7,9.4,9.5,10.1,10.5]
λ> frecuenciaDigitosPi 5000
[9.32,10.62,9.92,9.2,10.16,10.5,10.26,9.76,9.84,10.42]

Búsqueda en los dígitos de pi

José A. Alonso

15-02-2017

Misceláneas

El fichero Digitos_de_pi.txt contiene el número pi con un millón de decimales; es decir,

3.1415926535897932384626433832 ... 83996346460422090106105779458151

Definir la función

posicion :: String -> IO (Maybe Int)

tal que (posicion n) es (Just k) si k es la posición de n en la sucesión formada por un millón dígitos decimales del número pi y Nothing si n no ocurre en dicha sucesión. Por ejemplo,

λ> posicion "15"
Just 3
λ> posicion "2017"
Just 8897
λ> posicion "022017"
Just 382052
λ> posicion "14022017"
Nothing
λ> posicion "999999"
Just 762
λ> posicion "458151"
Just 999995

Cálculo de pi usando la fórmula de Vieta

José A. Alonso

14-02-2017

Misceláneas

La fórmula de Vieta para el cálculo de pi es la siguiente \[ \pi = 2 \times \frac{2}{\sqrt{2}} \times \frac{2}{\sqrt{2 + \sqrt{2}}} \times \frac{2}{\sqrt{2 + \sqrt{2 + \sqrt{2}}}} \times \frac{2}{\sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2}}}}} \times \cdots \]

Definir las funciones

aproximacionPi :: Int -> Double
errorPi :: Double -> Int

tales que

(aproximacionPi n) es la aproximación de pi usando n factores de la fórmula de Vieta. Por ejemplo,

aproximacionPi  5  ==  3.140331156954753
aproximacionPi 10  ==  3.1415914215112
aproximacionPi 15  ==  3.141592652386592
aproximacionPi 20  ==  3.1415926535886207
aproximacionPi 25  ==  3.141592653589795

(errorPi x) es el menor número de factores de la fórmula de Vieta necesarios para obtener pi con un error menor que x. Por ejemplo,

errorPi 0.1        ==  2
errorPi 0.01       ==  4
errorPi 0.001      ==  6
errorPi 0.0001     ==  7
errorPi 1e-4       ==  7
errorPi 1e-14      ==  24
pi                 ==  3.141592653589793
aproximacionPi 24  ==  3.1415926535897913

Cálculo de pi usando el producto de Wallis

José A. Alonso

13-02-2017

Misceláneas

El producto de Wallis es una expresión, descubierta por John Wallis en 1655, para representar el valor de π y que establece que: \[ \frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots \]

Definir las funciones

factoresWallis  :: [Rational]
productosWallis :: [Rational]
aproximacionPi  :: Int -> Double
errorPi         :: Double -> Int

tales que + factoresWallis es la sucesión de los factores del productos de Wallis. Por ejemplo,

λ> take 10 factoresWallis
[2 % 1,2 % 3,4 % 3,4 % 5,6 % 5,6 % 7,8 % 7,8 % 9,10 % 9,10 % 11]

productosWallis es la sucesión de los productos de los primeros factores de Wallis. Por ejemplo,

λ> take 7 productosWallis
[2 % 1,4 % 3,16 % 9,64 % 45,128 % 75,256 % 175,2048 % 1225]

(aproximacionPi n) es la aproximación de pi obtenida multiplicando los n primeros factores de Wallis. Por ejemplo,

aproximacionPi 20     ==  3.2137849402931895
aproximacionPi 200    ==  3.1493784731686008
aproximacionPi 2000   ==  3.142377365093878
aproximacionPi 20000  ==  3.141671186534396

(errorPi x) es el menor número de factores de Wallis necesarios para obtener pi con un error menor que x. Por ejemplo,

errorPi 0.1     ==  14
errorPi 0.01    ==  155
errorPi 0.001   ==  1569
errorPi 0.0001  ==  15707

Caminos en un árbol binario con suma dada

José A. Alonso

10-02-2017

Misceláneas

Los árboles binarios se pueden representar con el de tipo de dato algebraico

data Arbol = H
           | N Int Arbol Arbol
  deriving Show

Por ejemplo, los árboles

    3                7                 1
   / \              / \               /  \
  2   4            5   8             /    \
 / \   \          /   / \           /      \
1   7   5        6   4   9         3       -1
                                  / \     /  \
                                 2   1   4    5
                                    /   / \    \
                                   1   1   2    6

se representan por

ej1, ej2, ej3 :: Arbol
ej1 = N 3 (N 2 (N 1 H H) (N 7 H H)) (N 4 H (N 5 H H))
ej2 = N 7 (N 5 (N 6 H H) H) (N 8 (N 4 H H) (N 9 H H))
ej3 = N 1 (N 3 (N 2 H H) (N 1 (N 1 H H) H))
(N (-1) (N 4 (N 1 H H) (N 2 H H)) (N 5 H (N 6 H H)))

Definir las funciones

caminos     :: Arbol -> [[Int]]
caminosSuma :: Arbol -> Int -> [[Int]]

tales que

(caminos a) es la lista de los caminos entre dos nodos cualesquiera del árbol a. Por ejemplo,

λ> caminos ej1
[[3],[3,2],[3,2,1],[3,2,7],[3,4],[3,4,5],
 [2],[2,1],[2,7],[1],[7],[4],[4,5],[5]]
λ> caminos ej2
[[7],[7,5],[7,5,6],[7,8],[7,8,4],[7,8,9],
 [5],[5,6],[6],[8],[8,4],[8,9],[4],[9]]
λ> length (caminos ej3)
33

(caminosSuma a k) es la lista de los caminos entre dos nodos cualesquiera del árbol a cuya suma es k. Por ejemplo,

λ> caminosSuma ej1 3
[[3],[2,1]]
λ> caminosSuma ej3 3
[[3],[-1,4]]
λ> caminosSuma ej3 4
[[1,3],[1,-1,4],[3,1],[-1,4,1],[-1,5],[4]]
λ> caminosSuma ej3 5
[[1,3,1],[1,-1,4,1],[1,-1,5],[3,2],[3,1,1],[-1,4,2],[4,1],[5]]
λ> caminosSuma ej3 6
[[1,3,2],[1,3,1,1],[1,-1,4,2],[4,2],[6]]
λ> caminosSuma ej3 7
[]

Máximo común divisor de x e y veces n

José A. Alonso

09-02-2017

Misceláneas

Definir las funciones

repite :: Int -> Integer -> Integer
mcdR   :: Integer -> Int -> Int -> Integer

tales que

(repite x n) es el número obtenido repitiendo x veces el número n. Por ejemplo.

repite 3 123  ==  123123123

(mcdR n x y) es el máximo común divisor de los números obtenidos repitiendo x veces e y veces el número n. Por ejemplo.

mcdR 123 2 3                     ==  123
mcdR 4 4 6                       ==  44
mcdR 2017 (10^1000) (2+10^1000)  ==  20172017