Las expresiones aritméticas pueden representarse usando el siguiente tipo de datos

data Expr = N Int | S Expr Expr | P Expr Expr
  deriving (Eq, Ord, Show)

Por ejemplo, la expresión 2*(3+7) se representa por

P (N 2) (S (N 3) (N 7))

Definir la función

subexpresiones :: Expr -> Set Expr

tal que (subexpresiones e) es el conjunto de las subexpresiones de e. Por ejemplo,

λ> subexpresiones (S (N 2) (N 3))
fromList [N 2,N 3,S (N 2) (N 3)]
λ> subexpresiones (P (S (N 2) (N 2)) (N 7))
fromList [N 2,N 7,S (N 2) (N 2),P (S (N 2) (N 2)) (N 7)]

Leer más…

El número 23 se puede escribir de 4 formas como suma de sus dígitos

2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 3
2 + 2 + 2 + 2 + 2 + 2 + 2 + 3 + 3 + 3
2 + 2 + 2 + 2 + 3 + 3 + 3 + 3 + 3
2 + 3 + 3 + 3 + 3 + 3 + 3 + 3

La de menor número de sumando es la última, que tiene 8 sumandos.

Definir las funciones

minimoSumandosDigitos        :: Integer -> Integer
graficaMinimoSumandosDigitos :: Integer -> IO ()

tales que

• (minimoSumandosDigitos n) es el menor número de dígitos de n cuya suma es n. Por ejemplo,

minimoSumandosDigitos 23    ==  8
minimoSumandosDigitos 232   ==  78
minimoSumandosDigitos 2323  ==  775
map minimoSumandosDigitos [10..20] == [10,11,6,5,5,3,6,5,4,3,10]

• (graficaMinimoSumandosDigitos n) dibuja la gráfica de (minimoSumandosDigitos k) par los k primeros números naturales. Por ejemplo, (graficaMinimoSumandosDigitos 300) dibuja

Leer más…

Leer más…

La sucesión ECG estás definida por a(1) = 1, a(2) = 2 y, para n >= 3, a(n) es el menor natural que aún no está en la sucesión tal que a(n) tiene algún divisor común con a(n-1).

Los primeros términos de la sucesión son 1, 2, 4, 6, 3, 9, 12, 8, 10, 5, 15, ...

Al dibujar su gráfica, se parece a la de los electrocardiogramas (abreviadamente, ECG). Por ello, la sucesión se conoce como la sucesión ECG.

Definir las funciones

sucECG :: [Integer]
graficaSucECG :: Int -> IO ()

tales que

• sucECG es la lista de los términos de la sucesión ECG. Por ejemplo,

λ> take 20 sucECG
[1,2,4,6,3,9,12,8,10,5,15,18,14,7,21,24,16,20,22,11]
λ> sucECG !! 6000
6237

• (graficaSucECG n) dibuja la gráfica de los n primeros términos de la sucesión ECG. Por ejemplo, (graficaSucECG 160) dibuja

Leer más…

Una serie de potencias es una serie de la forma

a₀ + a₁x + a₂x² + a₃x³ + ...

Las series de potencias se pueden representar mediante listas infinitas. Por ejemplo, la serie de la función exponencial es

e^x = 1 + x + x²/2! + x³/3! + ...

y se puede representar por [1, 1, 1/2, 1/6, 1/24, 1/120, ...]

Las operaciones con series se pueden ver como una generalización de las de los polinomios.

En lo que sigue, usaremos el tipo (Serie a) para representar las series de potencias con coeficientes en a y su definición es

type Serie a = [a]

Definir las siguientes funciones

opuesta      :: Num a => Serie a -> Serie a
suma         :: Num a => Serie a -> Serie a -> Serie a
resta        :: Num a => Serie a -> Serie a -> Serie a
producto     :: Num a => Serie a -> Serie a -> Serie a
cociente     :: Fractional a => Serie a -> Serie a -> Serie a
derivada     :: (Num a, Enum a) => Serie a -> Serie a
integral     :: (Fractional a, Enum a) => Serie a -> Serie a
expx         :: Serie Rational

tales que

• (opuesta xs) es la opuesta de la serie xs. Por ejemplo,

λ> take 7 (opuesta [-6,-4..])
[6,4,2,0,-2,-4,-6]

• (suma xs ys) es la suma de las series xs e ys. Por ejemplo,

λ> take 7 (suma [1,3..] [2,4..])
[3,7,11,15,19,23,27]

• (resta xs ys) es la resta de las series xs es ys. Por ejemplo,

λ> take 7 (resta [3,5..] [2,4..])
[1,1,1,1,1,1,1]
λ> take 7 (resta ([3,7,11,15,19,23,27] ++ repeat 0) [1,3..])
[2,4,6,8,10,12,14]

• (producto xs ys) es el producto de las series xs e ys. Por ejemplo,

λ> take 7 (producto [3,5..] [2,4..])
[6,22,52,100,170,266,392]

• (cociente xs ys) es el cociente de las series xs e ys. Por ejemplo,

λ> take 7 (cociente ([6,22,52,100,170,266,392] ++ repeat 0) [3,5..])
[2.0,4.0,6.0,8.0,10.0,12.0,14.0]

• (derivada xs) es la derivada de la serie xs. Por ejemplo,

λ> take 7 (derivada [2,4..])
[4,12,24,40,60,84,112]

• (integral xs) es la integral de la serie xs. Por ejemplo,

λ> take 7 (integral ([4,12,24,40,60,84,112] ++ repeat 0))
[0.0,4.0,6.0,8.0,10.0,12.0,14.0]

• expx es la serie de la función exponencial. Por ejemplo,

λ> take 8 expx
[1 % 1,1 % 1,1 % 2,1 % 6,1 % 24,1 % 120,1 % 720,1 % 5040]
λ> take 8 (derivada expx)
[1 % 1,1 % 1,1 % 2,1 % 6,1 % 24,1 % 120,1 % 720,1 % 5040]
λ> take 8 (integral expx)
[0 % 1,1 % 1,1 % 2,1 % 6,1 % 24,1 % 120,1 % 720,1 % 5040]

Leer más…

Definir las funciones

grafo   :: [(Int,Int)] -> Grafo Int Int
caminos :: Grafo Int Int -> Int -> Int -> [[Int]]

tales que

• (grafo as) es el grafo no dirigido definido cuyas aristas son as. Por ejemplo,

λ> grafo [(2,4),(4,5)]
G ND (array (2,5) [(2,[(4,0)]),(3,[]),(4,[(2,0),(5,0)]),(5,[(4,0)])])

• (caminos g a b) es la lista los caminos en el grafo g desde a hasta b sin pasar dos veces por el mismo nodo. Por ejemplo,

λ> sort (caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 1 7)
[[1,3,5,7],[1,3,7]]
λ> sort (caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 2 7)
[[2,5,3,7],[2,5,7]]
λ> sort (caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 1 2)
[[1,3,5,2],[1,3,7,5,2]]
λ> caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 1 4
[]
λ> length (caminos (grafo [(i,j) | i <- [1..10], j <- [i..10]]) 1 10)
109601

Leer más…

Definir la función

sinDobleCero :: Int -> [[Int]]

tal que (sinDobleCero n) es la lista de las listas de longitud n formadas por el 0 y el 1 tales que no contiene dos ceros consecutivos. Por ejemplo,

ghci> sinDobleCero 2
[[1,0],[1,1],[0,1]]
ghci> sinDobleCero 3
[[1,1,0],[1,1,1],[1,0,1],[0,1,0],[0,1,1]]
ghci> sinDobleCero 4
[[1,1,1,0],[1,1,1,1],[1,1,0,1],[1,0,1,0],[1,0,1,1],
 [0,1,1,0],[0,1,1,1],[0,1,0,1]]

Leer más…

Para cada entero positivo n, existe una única sucesión que empieza en 1, termina en n y en la que cada uno de sus elementos es el doble de su anterior o el doble más uno. Dicha sucesión se llama la sucesión duplicadora de n. Por ejemplo, la sucesión duplicadora de 13 es [1, 3, 6, 13], ya que

 3 = 2*1 +1
 6 = 2*3
13 = 2*6 +1

Definir la función

duplicadora :: Integer -> [Integer]

tal que (duplicadora n) es la sucesión duplicadora de n. Por ejemplo,

duplicadora 13                   ==  [1,3,6,13]
duplicadora 17                   ==  [1,2,4,8,17]
length (duplicadora (10^40000))  ==  132878

Leer más…

El complemento de un número positivo x se calcula por el siguiente procedimiento:

• si x es mayor que 9, se toma cada dígito por su valor posicional y se resta del mayor los otro dígitos. Por ejemplo, el complemento de 1448 es 1000 - 400 - 40 - 8 = 552. Para
• si x es menor que 10, su complemento es x.

Definir las funciones

cadena    :: Integer -> [Integer]
conCadena :: Int -> [Integer]

tales que

• (cadena x) es la cadena de primos a partir de x tal que cada uno es el complemento del anterior. Por ejemplo,

cadena 8         == []
cadena 7         == [7]
cadena 13        == [13,7]
cadena 643       == [643,557,443]
cadena 18127     == [18127,1873,127,73,67,53,47]
cadena 18181213  == [18181213,1818787,181213,18787,1213,787,613,587]

• (conCadena n) es la lista de números cuyas cadenas tienen n elementos. Por ejemplo,

take 6 (conCadena 3)                == [23,31,61,67,103,307]
[head (conCadena n) | n <- [4..8]]  == [37,43,157,18127,181873]

Leer más…

La sucesión de Loomis generada por un número entero positivo x es la sucesión cuyos términos se definen por

• f(0) es x
• f(n) es la suma de f(n-1) y el producto de los dígitos no nulos de f(n-1)

Los primeros términos de las primeras sucesiones de Loomis son

• Generada por 1: 1, 2, 4, 8, 16, 22, 26, 38, 62, 74, 102, 104, 108, 116, 122, ...
• Generada por 2: 2, 4, 8, 16, 22, 26, 38, 62, 74, 102, 104, 108, 116, 122, 126, ...
• Generada por 3: 3, 6, 12, 14, 18, 26, 38, 62, 74, 102, 104, 108, 116, 122, 126, ...
• Generada por 4: 4, 8, 16, 22, 26, 38, 62, 74, 102, 104, 108, 116, 122, 126, 138, ...
• Generada por 5: 5, 10, 11, 12, 14, 18, 26, 38, 62, 74, 102, 104, 108, 116, 122, ...

Se observa que a partir de un término todas coinciden con la generada por 1. Dicho término se llama el punto de convergencia. Por ejemplo,

• la generada por 2 converge a 2
• la generada por 3 converge a 26
• la generada por 4 converge a 4
• la generada por 5 converge a 26

Definir las siguientes funciones

omis           :: Integer -> [Integer]
rgencia        :: Integer -> Integer
caConvergencia :: [Integer] -> IO ()

 que

cLoomis x) es la sucesión de Loomis generada por x. Por ejemplo,

λ> take 15 (sucLoomis 1)
[1,2,4,8,16,22,26,38,62,74,102,104,108,116,122]
λ> take 15 (sucLoomis 2)
[2,4,8,16,22,26,38,62,74,102,104,108,116,122,126]
λ> take 15 (sucLoomis 3)
[3,6,12,14,18,26,38,62,74,102,104,108,116,122,126]
λ> take 15 (sucLoomis 4)
[4,8,16,22,26,38,62,74,102,104,108,116,122,126,138]
λ> take 15 (sucLoomis 5)
[5,10,11,12,14,18,26,38,62,74,102,104,108,116,122]
λ> take 15 (sucLoomis 20)
[20,22,26,38,62,74,102,104,108,116,122,126,138,162,174]
λ> take 15 (sucLoomis 100)
[100,101,102,104,108,116,122,126,138,162,174,202,206,218,234]
λ> sucLoomis 1 !! (2*10^5)
235180736652

• (convergencia x) es el término de convergencia de la sucesioń de Loomis generada por x xon la geerada por 1. Por ejemplo,

convergencia  2      ==  2
convergencia  3      ==  26
convergencia  4      ==  4
convergencia 17      ==  38
convergencia 19      ==  102
convergencia 43      ==  162
convergencia 27      ==  202
convergencia 58      ==  474
convergencia 63      ==  150056
convergencia 81      ==  150056
convergencia 89      ==  150056
convergencia (10^12) ==  1000101125092

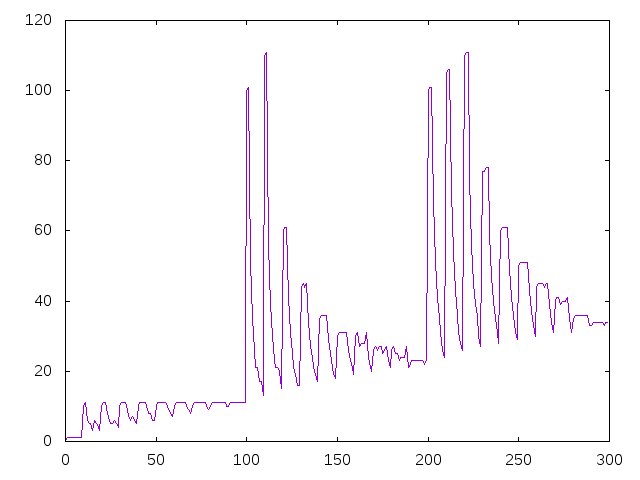
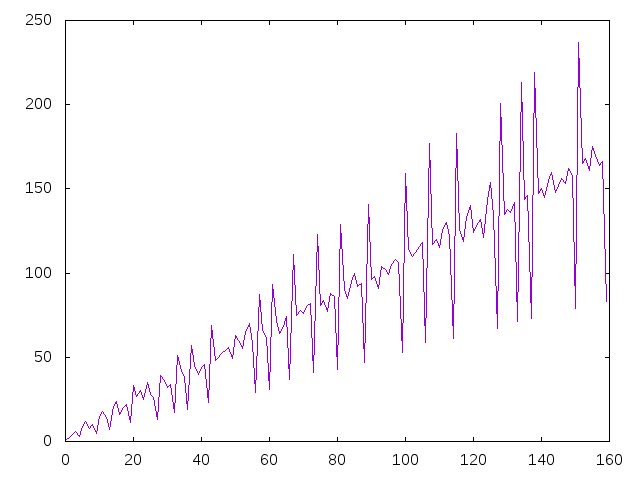
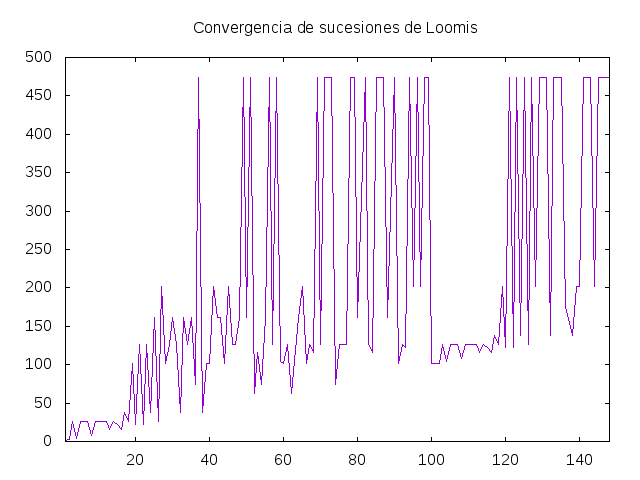
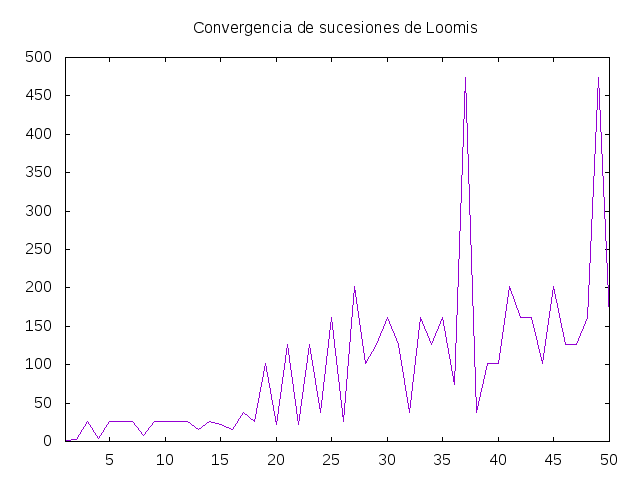• (graficaConvergencia xs) dibuja la gráfica de los términos de convergencia de las sucesiones de Loomis generadas por los elementos de xs. Por ejemplo, (graficaConvergencia ([1..50]) dibuja y graficaConvergencia ([1..148] \ [63,81,89,137]) dibuja

Leer más…