Suma de intervalos
Los intervalos se pueden representar por pares de enteros (a,b) con a < b. Los elementos del intervalo (2,5) son 2, 3, 4 y 5; por tanto, su longitud es 4. Para calcular la suma de los longitudes de una lista de intervalos hay que tener en cuenta de quw si hay intervalos superpuestos sus elementos deben de contarse sólo una vez. Por ejemplo, la suma de los intervalos de [(1,4),(7,10),(3,5)] es 7 ya que, como los intervalos (1,4) y (3,5) se solapan, los podemos ver como el intervalo (1,5) que tiene una longitud de 4.
Definir la función
sumaIntervalos :: [(Int, Int)] -> Int
tal que (sumaIntervalos xs) es la suma de las longitudes de los intervalos de xs contando los superpuestos sólo una vez. Por ejemplo,
sumaIntervalos [(1, 5)] == 4 sumaIntervalos [(1, 5), (6, 10)] == 8 sumaIntervalos [(1, 5), (5, 10)] == 9 sumaIntervalos [(1, 5), (1, 5)] == 4 sumaIntervalos [(1, 4), (7, 10), (3, 5)] == 7
Búsqueda de la mina
En este ejercicio, se representa un mapa mediante una lista de listas de la misma longitud donde todos sus elementos son 0 menos uno (que es un 1) que es donde se encuentra la mina. Por ejemplo, en el mapa
0 0 0 0 0 0 0 0 0 1 0 0
la posición de la mina es (2,1).
Definir la función
posicionMina :: [[Int]] -> (Int,Int)
tal que (posicionMina m) es la posición de la mina en el mapa m, Por ejemplo,
posicionMina [[0,0,0,0],[0,0,0,0],[0,1,0,0]] == (2,1)
El sesgo de Chebyshev
Un número primo distinto de 2 tiene la forma 4k + 1 o 4k + 3. Chebyshev notó en 1853 que la mayoría de las veces hay más números primos de la forma 4k + 3 que números primos de la forma 4k + 1 menores que un número dado. Esto se llama el sesgo de Chebyshev.
Definir las funciones
distribucionPrimosModulo4 :: [(Integer, Integer, Integer)] empatesRestosModulo4 :: [Integer] mayoria1RestosModulo4 :: [Integer] grafica_Chebyshev :: Int -> IO ()
tales que
- distribucionPrimosModulo4 es la lista de las ternas (p,a,b) tales que p es un números primo, a es la cantidad de primos menores o iguales que p congruentes con 1 módulo 4 y b es la cantidad de primos menores o iguales que p congruentes con 3 módulo 4. Por ejemplo,
λ> take 7 distribucionPrimosModulo4 [(2,0,0),(3,0,1),(5,1,1),(7,1,2),(11,1,3),(13,2,3),(17,3,3)] λ> distribucionPrimosModulo4 !! (5*10^5) (7368791,249888,250112)
- empatesRestosModulo4 es la lista de los primos p tales que la cantidad de primos menores o iguales que p congruentes con 1 módulo 4 es igual a la cantidad de primos menores o iguales que p congruentes con 3 módulo 4. Por ejemplo,
λ> take 10 empatesRestosModulo4 [2,5,17,41,461,26833,26849,26863,26881,26893] λ> length (takeWhile (<= 10^6) empatesRestosModulo4) 112
- mayoria1RestosModulo4 es la lista de los primos p tales que la cantidad de primos menores o iguales que p congruentes con 1 módulo 4 es mayor que la cantidad de primos menores o iguales que p congruentes con 3 módulo 4. Por ejemplo,
λ> take 10 mayoria1RestosModulo4 [26861,616841,616849,616877,616897,616909,616933,616943,616951,616961] λ> length (takeWhile (<= 10^6) mayoria1RestosModulo4) 239
- (graficaChebyshev n) dibuja la gráfica de los puntos (p,b-a) donde p es uno de los n primeros primos impares, a es la cantidad de primos menores o iguales que p congruentes con 1 módulo 4 y b es la cantidad de primos menores o iguales que p congruentes con 3 módulo 4. Por ejemplo, (graficaChebyshev 5000) dibuja la figura
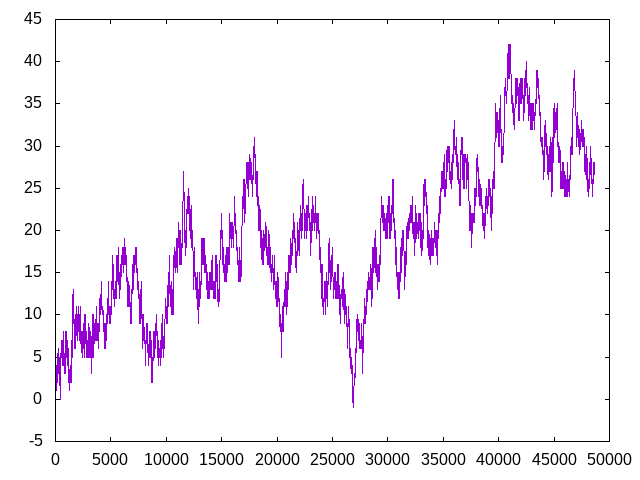
Primos magnánimos
Un número magnánimo es un número tal que las sumas obtenidas insertando un "+" entre sus dígitos en cualquier posición son números primos. Por ejemplo, 4001 es un número magnánimo porque los números 4+001=5, 40+01=41 y 400+1=401 son primos.
Definir las funciones
esMagnanimo :: Integer -> Bool primosMagnanimos :: [Integer]
tales que
- (esMagnanimo n) se verifica si n es un número magnánimo. Por ejemplo,
esMagnanimo 4001 == True esMagnanimo 2019 == False
- primosMagnanimos es la lista de los números primos magnánimos. Por ejemplo,
λ> take 20 primosMagnanimos [2,3,5,7,11,23,29,41,43,47,61,67,83,89,101,227,229,281,401,443]
Diagonales invertidas
Definir la función
diagonalesInvertidas :: Matrix a -> Matrix a
tal que (diagonalesInvertidas q) es la matriz obtenida invirtiendo el orden de los elementos de la diagonal principal y de la diagonal secundaria de q. Por ejemplo,
λ> fromList 5 5 [1..] ┌ ┐ │ 1 2 3 4 5 │ │ 6 7 8 9 10 │ │ 11 12 13 14 15 │ │ 16 17 18 19 20 │ │ 21 22 23 24 25 │ └ ┘ λ> diagonalesInvertidas (fromList 5 5 [1..]) ┌ ┐ │ 25 2 3 4 21 │ │ 6 19 8 17 10 │ │ 11 12 13 14 15 │ │ 16 9 18 7 20 │ │ 5 22 23 24 1 │ └ ┘ λ> fromList 3 3 ['a','b'..] ┌ ┐ │ 'a' 'b' 'c' │ │ 'd' 'e' 'f' │ │ 'g' 'h' 'i' │ └ ┘ λ> diagonalesInvertidas (fromList 3 3 ['a','b'..]) ┌ ┐ │ 'i' 'b' 'g' │ │ 'd' 'e' 'f' │ │ 'c' 'h' 'a' │ └ ┘
Cálculo de pi mediante el método de Newton
El método de Newton para el cálculo de pi se basa en la relación
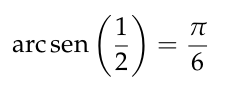
y en el desarrollo del arco seno
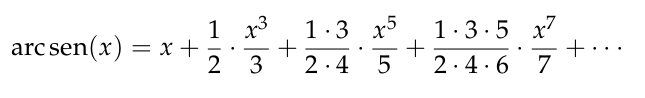
de donde se obtiene la fórmula
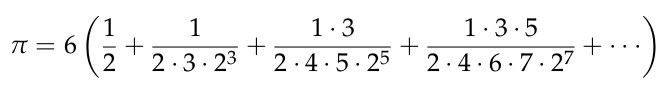
La primeras aproximaciones son
a(0) = 6*(1/2) = 3.0 a(1) = 6*(1/2+1/(2*3*2^3)) = 3.125 a(2) = 6*(1/2+1/(2*3*2^3)+(1*3)/(2*4*5*2^5)) = 3.1390625
Definir las funciones
aproximacionPi :: Int -> Double grafica :: [Int] -> IO ()
tales que
- (aproximacionPi n) es la n-ésima aproximación de pi con la fórmula de Newton. Por ejemplo,
aproximacionPi 0 == 3.0 aproximacionPi 1 == 3.125 aproximacionPi 2 == 3.1390625 aproximacionPi 10 == 3.1415926468755613 aproximacionPi 21 == 3.141592653589793 pi == 3.141592653589793
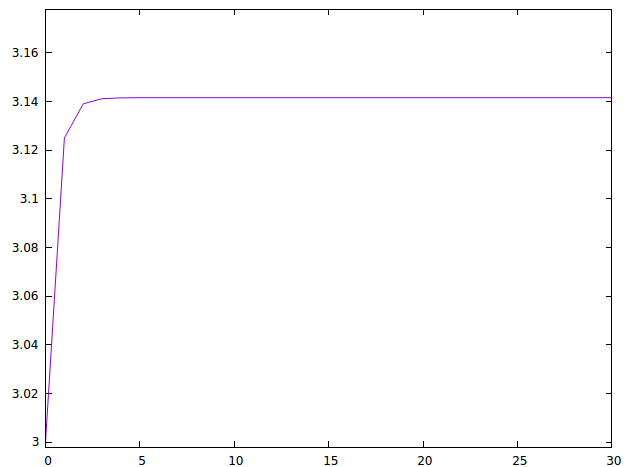
- (grafica xs) dibuja la gráfica de las k-ésimas aproximaciones de pi donde k toma los valores de la lista xs. Por ejemplo, (grafica [1..30]) dibuja
Repeticiones consecutivas
Se dice que una palabra tiene una repetición en una frase si es igual a una, o más, de las palabras consecutivas sin distinguir mayúsculas de minúsculas.
Definir la función
nRepeticionesConsecutivas :: String ->Int
tal que (nRepeticionesConsecutivas cs) es el número de repeticiones de palabras consecutivas de la cadena cs. Por ejemplo,
nRepeticionesConsecutivas "oso rana" == 0 nRepeticionesConsecutivas "oso rana oso" == 0 nRepeticionesConsecutivas "oso oSo rana" == 1 nRepeticionesConsecutivas "oso oso oso rana" == 1 nRepeticionesConsecutivas "coronavirus virus oso rana" == 0 nRepeticionesConsecutivas "virus virus oso rana" == 1 nRepeticionesConsecutivas "virus oso virus oso rana" == 0 nRepeticionesConsecutivas "oso oso oso oso oso oso" == 1 nRepeticionesConsecutivas "oso oso oso oso rana rana" == 2 nRepeticionesConsecutivas "rana rana oso oso rana rana" == 3
Medias de dígitos de pi
El fichero Digitos_de_pi.txt contiene el número pi con un millón de decimales; es decir,
3.1415926535897932384626433832 ... 83996346460422090106105779458151
Definir las funciones
mediasDigitosDePi :: IO [Double] graficaMediasDigitosDePi :: Int -> IO ()
tales que
- mediasDigitosDePi es la sucesión cuyo n-ésimo elemento es la media de los n primeros dígitos de pi. Por ejemplo,
λ> xs <- mediasDigitosDePi λ> take 5 xs [1.0,2.5,2.0,2.75,4.0] λ> take 10 xs [1.0,2.5,2.0,2.75,4.0,3.6666666666666665,4.0,4.125,4.0,4.1] λ> take 10 <$> mediasDigitosDePi [1.0,2.5,2.0,2.75,4.0,3.6666666666666665,4.0,4.125,4.0,4.1]
- (graficaMediasDigitosDePi n) dibuja la gráfica de los n primeros términos de mediasDigitosDePi. Por ejemplo,
- (graficaMediasDigitosDePi 20) dibuja
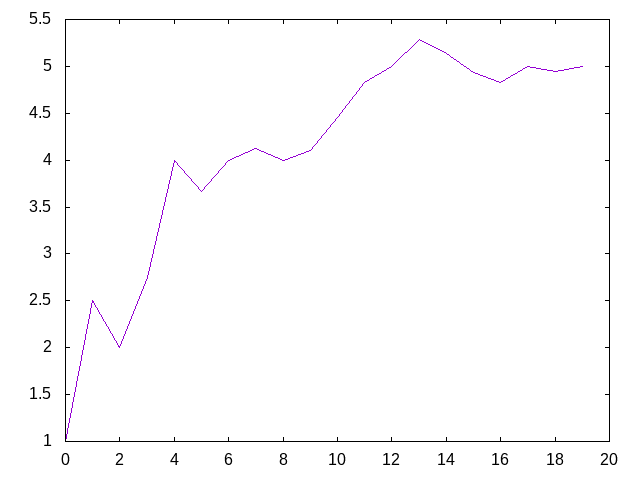
- (graficaMediasDigitosDePi 200) dibuja
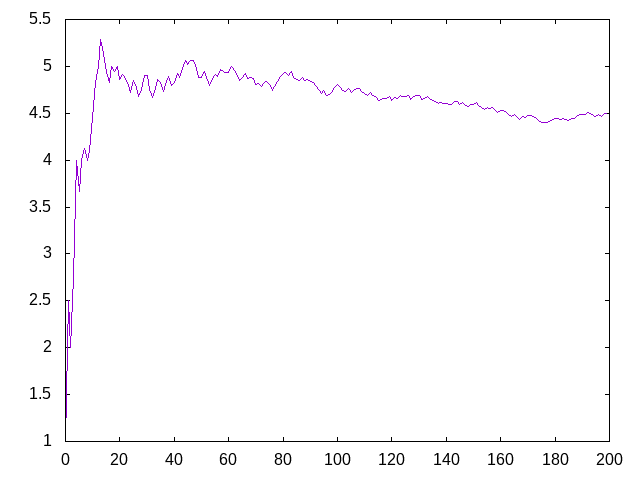
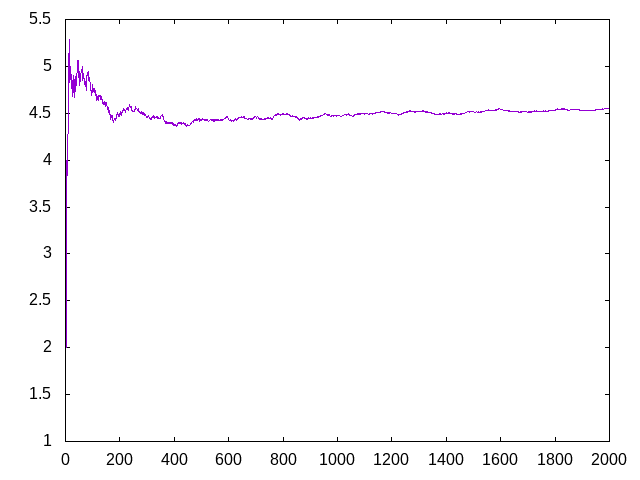
- (graficaMediasDigitosDePi 2000) dibuja
Distancia esperada entre dos puntos de un cuadrado unitario
Definir, por simulación, la función
distanciaEsperada :: Int -> IO Double
tal que (distanciaEsperada n) es la distancia esperada entre n puntos del cuadrado unitario de vértices opuestos (0,0) y (1,1), elegidos aleatoriamente. Por ejemplo,
distanciaEsperada 10 == 0.43903617921423593 distanciaEsperada 10 == 0.6342350621260004 distanciaEsperada 100 == 0.5180418995364429 distanciaEsperada 100 == 0.5288261085653962 distanciaEsperada 1000 == 0.5143804432569616 distanciaEsperada 10000 == 0.5208360147922616
El valor exacto de la distancia esperada es
ve = (sqrt(2) + 2 + 5*log(1+sqrt(2)))/15 = 0.5214054331647207
Definir la función
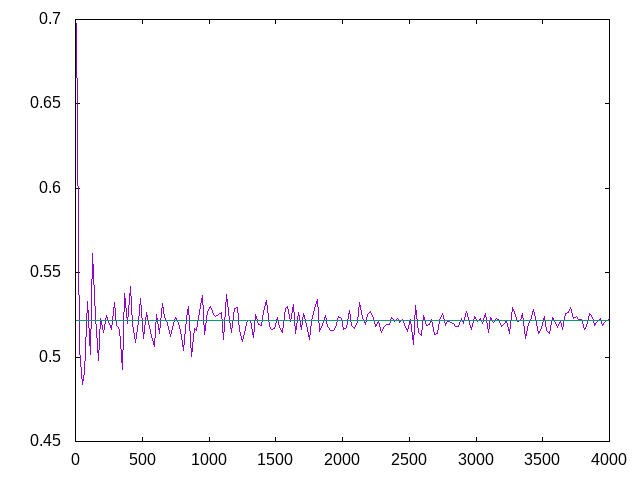
graficaDistanciaEsperada :: [Int] -> IO ()
tal que (graficaDistanciaEsperadan n) dibuja las gráficas de los pares (n, distanciaEsperada n) para n en la lista creciente ns junto con la recta y = ve, donde ve es el valor exacto. Por ejemplo, (graficaDistanciaEsperada [10,30..4000]) dibuja