El día 11 de noviembre, se publicó en la cuenta de Twitter de Fermat's Library la siguiente curiosa identidad que relaciona los números e y pi:

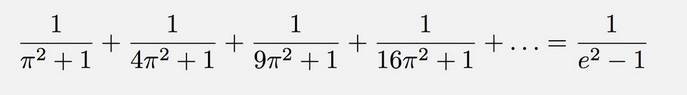
Definir las siguientes funciones:

sumaTerminos :: Int -> Double
aproximacion :: Double -> Int

tales que

• (sumaTerminos n) es la suma de los primeros n términos de la serie 1/(π²+ 1) + 1/(4π²+1) + 1/(9π²+1) + 1/(16π²+ ) + ... Por ejemplo,

sumaTerminos 10     ==  0.14687821811081034
sumaTerminos 100    ==  0.15550948345688423
sumaTerminos 1000   ==  0.15641637221314514
sumaTerminos 10000  ==  0.15650751113789382

• (aproximación x) es el menor número de términos que hay que sumar de la serie anterior para que se diferencie (en valor absoluto) de 1/(e²-1) menos que x. Por ejemplo,

aproximacion 0.1     ==  1
aproximacion 0.01    ==  10
aproximacion 0.001   ==  101
aproximacion 0.0001  ==  1013

Leer más…

Un árbol binario completo es un árbol binario que tiene todos los nodos posibles hasta el penúltimo nivel, y donde los elementos del último nivel están colocados de izquierda a derecha sin dejar huecos entre ellos.

La numeración de los árboles binarios completos se realiza a partir de la raíz, recorriendo los niveles de izquierda a derecha. Por ejemplo,

        1
       /  \
      /    \
     /      \
    2        3
   / \      / \
  4   5    6   7
 / \
8   9

Los árboles binarios se puede representar mediante el siguiente tipo

data Arbol = H
           | N Integer Arbol Arbol
  deriving (Show, Eq)

Cada posición de un elemento de un árbol es una lista de movimientos hacia la izquierda o hacia la derecha. Por ejemplo, la posición de 9 en al árbol anterior es [I,I,D].

Los tipos de los movimientos y de las posiciones se definen por

data Movimiento = I | D deriving (Show, Eq)
type Posicion   = [Movimiento]

Definir la función

elementoEnPosicion :: Posicion -> Integer

tal que (elementoEnPosicion ms) es el elemento en la posición ms. Por ejemplo,

elementoEnPosicion [D,I]    ==  6
elementoEnPosicion [D,D]    ==  7
elementoEnPosicion [I,I,D]  ==  9
elementoEnPosicion []       ==  1

Leer más…

Un árbol binario completo es un árbol binario que tiene todos los nodos posibles hasta el penúltimo nivel, y donde los elementos del último nivel están colocados de izquierda a derecha sin dejar huecos entre ellos.

La numeración de los árboles binarios completos se realiza a partir de la raíz, recorriendo los niveles de izquierda a derecha. Por ejemplo,

        1
       /  \
      /    \
     /      \
    2        3
   / \      / \
  4   5    6   7
 / \
8   9

Los árboles binarios se puede representar mediante el siguiente tipo

data Arbol = H
           | N Integer Arbol Arbol
  deriving (Show, Eq)

Cada posición de un elemento de un árbol es una lista de movimientos hacia la izquierda o hacia la derecha. Por ejemplo, la posición de 9 en al árbol anterior es [I,I,D].

Los tipos de los movimientos y de las posiciones se definen por

data Movimiento = I | D deriving (Show, Eq)
type Posicion   = [Movimiento]

Definir la función

posicionDeElemento :: Integer -> Posicion

tal que (posicionDeElemento n) es la posición del elemento n en el árbol binario completo. Por ejemplo,

posicionDeElemento 6  ==  [D,I]
posicionDeElemento 7  ==  [D,D]
posicionDeElemento 9  ==  [I,I,D]
posicionDeElemento 1  ==  []

length (posicionDeElemento2 (10^50000))  ==  166096

Leer más…

Los árboles binarios con datos en los nodos se definen por

data Arbol a = H
             | N a (Arbol a) (Arbol a)
  deriving (Eq, Show)

Por ejemplo, el árbol

       3
      / \
     /   \
    0     5
   / \   / \
  5   4 0   3
 / \
2   0

se representa por

ejArbol :: Arbol Int
ejArbol = N 3
            (N 0
               (N 5
                  (N 2 H H)
                  (N 4 H H))
               (N 0 H H))
            (N 5
               (N 0 H H)
               (N 3 H H))

Cada posición de un elemento de un árbol es una lista de movimientos hacia la izquierda o hacia la derecha. Por ejemplo, la posición de 4 en al árbol anterior es [I,I,D].

Los tipos de los movimientos y de las posiciones se definen por

data Movimiento = I | D deriving (Show, Eq)
type Posicion   = [Movimiento]

Definir la función

posiciones :: Eq b => b -> Arbol b -> [Posicion]

tal que (posiciones n a) es la lista de las posiciones del elemento n en el árbol a. Por ejemplo,

posiciones 0 ejArbol  ==  [[I],[I,D],[D,I]]
posiciones 2 ejArbol  ==  [[I,I,I]]
posiciones 3 ejArbol  ==  [[],[D,D]]
posiciones 4 ejArbol  ==  [[I,I,D]]
posiciones 5 ejArbol  ==  [[I,I],[D]]
posiciones 1 ejArbol  ==  []

Leer más…

Un árbol binario completo es un árbol binario que tiene todos los nodos posibles hasta el penúltimo nivel, y donde los elementos del último nivel están colocados de izquierda a derecha sin dejar huecos entre ellos.

La numeración de los árboles binarios completos se realiza a partir de la raíz, recorriendo los niveles de izquierda a derecha. Por ejemplo,

        1
       /  \
      /    \
     /      \
    2        3
   / \      / \
  4   5    6   7
 / \
8   9

Los árboles binarios se puede representar mediante el siguiente tipo

data Arbol = H
           | N Int Arbol Arbol
  deriving (Show, Eq)

Definir la función

arbolBinarioCompleto :: Int -> Arbol

tal que (arbolBinarioCompleto n) es el árbol binario completo con n nodos. Por ejemplo,

λ> arbolBinarioCompleto 4
N 1 (N 2 (N 4 H H) H) (N 3 H H)
λ> arbolBinarioCompleto 9
N 1
  (N 2
     (N 4
        (N 8 H H)
        (N 9 H H))
     (N 5 H H))
  (N 3
     (N 6 H H)
     (N 7 H H))

Leer más…

Un número x es un cubo si existe un y tal que x = y^3. Por ejemplo, 8 es un cubo porque 8 = 2^3.

Definir la función

raizCubicaEntera :: Integer -> Maybe Integer.

tal que (raizCubicaEntera x n) es justo la raíz cúbica del número natural x, si x es un cubo y Nothing en caso contrario. Por ejemplo,

raizCubicaEntera 8             ==  Just 2
raizCubicaEntera 9             ==  Nothing
raizCubicaEntera 27            ==  Just 3
raizCubicaEntera 64            ==  Just 4
raizCubicaEntera (2^30)        ==  Just 1024
raizCubicaEntera (10^9000)     ==  Just (10^3000)
raizCubicaEntera (5 + 10^9000) ==  Nothing

Leer más…

Se dice que un número natural n es una colina si su primer dígito es igual a su último dígito, los primeros dígitos son estrictamente creciente hasta llegar al máximo, el máximo se puede repetir y los dígitos desde el máximo al final son estrictamente decrecientes.

Definir la función

esColina :: Integer -> Bool

tal que (esColina n) se verifica si n es un número colina. Por ejemplo,

esColina 12377731  ==  True
esColina 1237731   ==  True
esColina 123731    ==  True
esColina 12377730  ==  False
esColina 12377730  ==  False
esColina 10377731  ==  False
esColina 12377701  ==  False
esColina 33333333  ==  True

Leer más…

Definir la función

solitario :: Ord a => [a] -> a

tal que (solitario xs) es el único elemento que ocurre una vez en la lista xs (se supone que la lista xs tiene al menos 3 elementos y todos son iguales menos uno que es el solitario). Por ejemplo,

solitario [2,2,7,2]  ==  7
solitario [2,2,2,7]  ==  7
solitario [7,2,2,2]  ==  7
solitario (replicate (2*10^7) 1 ++ [2])  ==  2

Leer más…

Esta semana se ha publicado en Twitter una demostración visual de la suma de inversos de potencias de 4:

1/4 + 1/4² + 1/4³ + ... = 1/3

Definir las funciones

sumaInversosPotenciasDeCuatro :: [Double]
aproximacion :: Double -> Int

tales que

• sumaInversosPotenciasDeCuatro es la lista de las suma de la serie de los inversos de las potencias de cuatro. Por ejemplo,

λ> take 6 sumaInversosPotenciasDeCuatro
[0.25,0.3125,0.328125,0.33203125,0.3330078125,0.333251953125]

• (aproximacion e) es el menor número de términos de la serie anterior que hay que sumar para que el valor absoluto de su diferencia con 1/3 sea menor que e. Por ejemplo,

aproximacion 0.001  ==  4
aproximacion 1e-3   ==  4
aproximacion 1e-6   ==  9
aproximacion 1e-20  ==  26
sumaInversosPotenciasDeCuatro !! 26  ==  0.3333333333333333

Leer más…

Definir las funciones

esPrimoSumaDeDosPrimos :: Integer -> Bool

primosSumaDeDosPrimos :: [Integer] tales que

• (esPrimoSumaDeDosPrimos x) se verifica si x es un número primo que se puede escribir como la suma de dos números primos. Por ejemplo,

esPrimoSumaDeDosPrimos 19  ==  True
esPrimoSumaDeDosPrimos 20  ==  False
esPrimoSumaDeDosPrimos 23  ==  False

• primosSumaDeDosPrimos es la lista de los números primos que se pueden escribir como la suma de dos números primos. Por ejemplo,

λ> take 17 primosSumaDeDosPrimos
[5,7,13,19,31,43,61,73,103,109,139,151,181,193,199,229,241]
λ> primosSumaDeDosPrimos !! (10^5)
18409543

Leer más…