Definir las funciones

menorPotencia            :: Integer -> (Integer,Integer)
graficaMenoresExponentes :: Integer -> IO ()

tales que

• (menorPotencia n) es el par (k,m) donde m es la menor potencia de 2 que empieza por n y k es su exponentes (es decir, 2^k = m). Por ejemplo,

menorPotencia 3             ==  (5,32)
menorPotencia 7             ==  (46,70368744177664)
fst (menorPotencia 982)     ==  3973
fst (menorPotencia 32627)   ==  28557
fst (menorPotencia 158426)  ==  40000

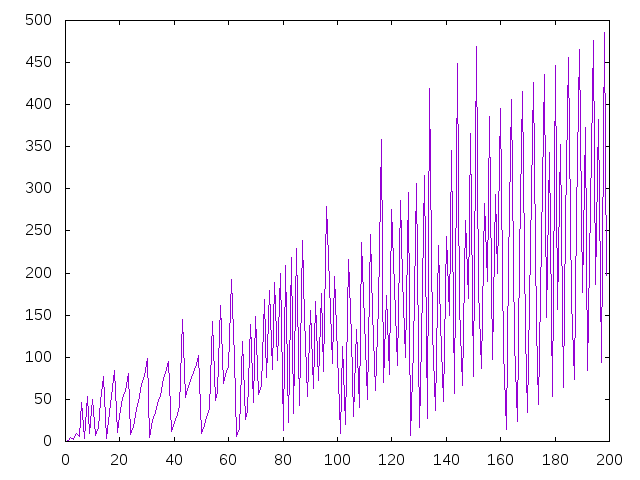
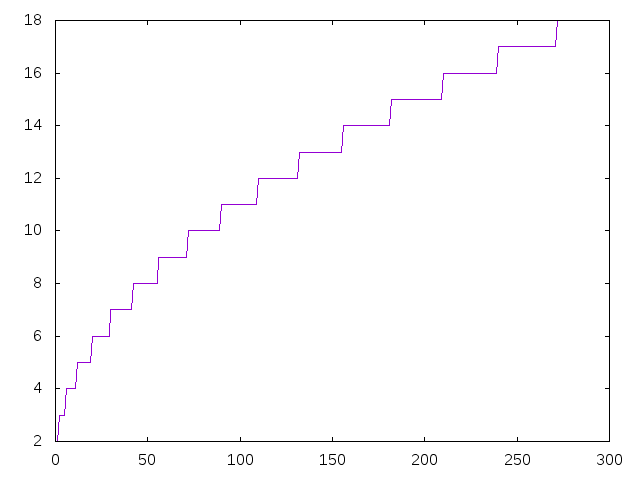
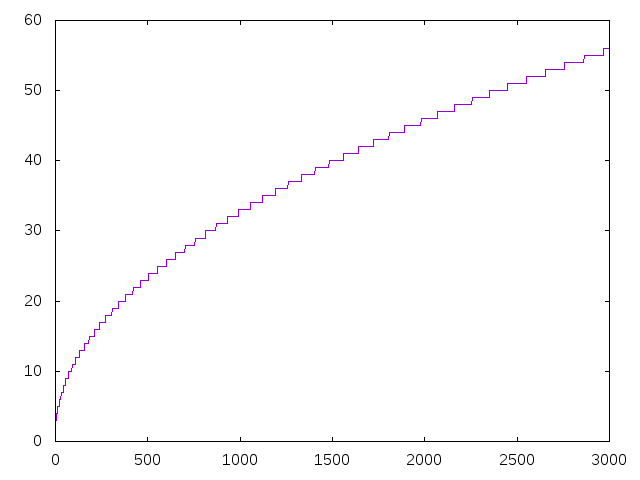
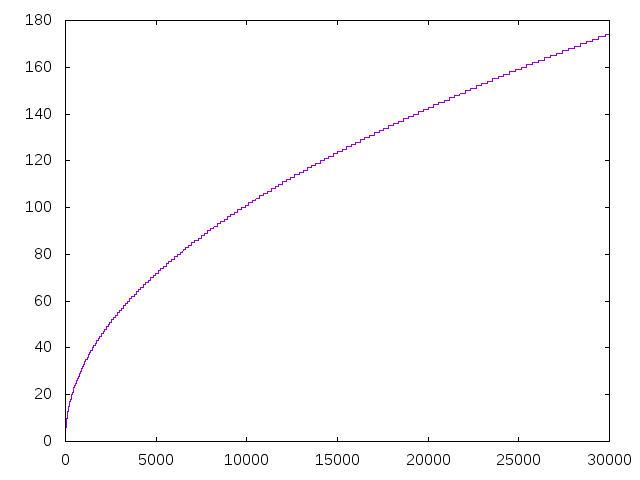
• (graficaMenoresExponentes n) dibuja la gráfica de los exponentes de 2 en las menores potencias de los n primeros números enteros positivos. Por ejemplo, (graficaMenoresExponentes 200) dibuja

Leer más…

En el ejercicio anterior se explicó una representación reducida de las matrices dispersas. A partir del número de columnas y la representación reducida se puede construir la matriz.

Definir la función

ampliada :: Num a => Int -> [[(Int,a)]] -> Matrix a

tal que (ampliada n xss) es la matriz con n columnas cuya representación reducida es xss. Por ejemplo,

λ> ampliada 3 [[(3,4)],[(2,5)],[]]
( 0 0 4 )
( 0 5 0 )
( 0 0 0 )

λ> ampliada 3 [[],[]]
( 0 0 0 )
( 0 0 0 )

λ> ampliada 2 [[],[],[]]
( 0 0 )
( 0 0 )
( 0 0 )

Leer más…

Una representación reducida de una matriz dispersa es una lista de listas donde cada una de las listas representa una fila de la matriz mediante listas de pares correspondientes a las snúmeros de columnas con valores no nulos de la matriz. Por ejemplo, la representación reducida de la matriz

( 0 0 4 )
( 0 5 0 )
( 0 0 0 )

es [[(3,4)],[(2,5)],[]].

Definir la función

reducida :: (Num a, Eq a) => Matrix a -> [[(Int,a)]]

tal que (reducida p) es la representación reducida de la matriz p. Por ejemplo,

reducida (fromList 3 3 [0,0,4,0,5,0,0,0,0])  ==  [[(3,4)],[(2,5)],[]]
reducida (identity 3)  ==  [[(1,1)],[(2,1)],[(3,1)]]
reducida (zero 9 3)    ==  [[],[],[],[],[],[],[],[],[]]
reducida (zero 9 4)    ==  [[],[],[],[],[],[],[],[],[]]

Leer más…

Una matriz es dispersa si la mayoriá de sus elementos son ceros. Por ejemplo, la primera de las siguientes matrices es dispersa y la segunda no lo es

( 0 0 4 )   ( 0 1 4 )
( 0 5 0 )   ( 0 5 1 )
( 0 0 0 )

Usando la librería Data.Matrix, las anteriores matrices se pueden definir por

ej1, ej2 :: Matrix Int
ej1 = fromList 3 3 [0,0,4,0,5,0,0,0,0]
ej2 = fromList 2 3 [0,1,4,0,5,1]

La dispersión de una matriz es el cociente entre el número de ceros de la matriz y el producto de sus números de filas y de columnas.

Definir las siguientes funciones

dispersion :: (Num a, Eq a) => Matrix a -> Double
esDispersa :: (Num a, Eq a) => Matrix a -> Bool

tales que

• (dispersion p) es la dispersión de la matriz p. Por ejemplo,

dispersion ej1              ==  0.7777777777777778
dispersion ej2              ==  0.3333333333333333
dispersion (fmap (+1) ej1)  ==  0.0
dispersion (identity 3)     ==  0.6666666666666666
dispersion (zero 9 9)       ==  1.0

• (esDispersa p) se verifica si la matriz p es dispersa. Por ejemplo,

esDispersa ej1              ==  True
esDispersa ej2              ==  False
esDispersa (fmap (+1) ej1)  ==  False
esDispersa (identity 3)     ==  True
esDispersa (zero 9 9)       ==  True

Leer más…

Definir la función

esCuadrado :: (Num a, Ord a) => (a,a) -> (a,a) -> (a,a) -> (a,a) -> Bool

tal que (esCuadrado p q r s) se verifica si los puntos p, q, r y s son los vértices de un cuadrado. Por ejemplo,

esCuadrado (0,0) (0,1) (1,1) (1,0)    == True
esCuadrado (0,0) (2,1) (3,-1) (1, -2) == True
esCuadrado (0,0) (1,1) (0,1) (1,0)    == True
esCuadrado (1,1) (1,1) (1,1) (1,1)    == True
esCuadrado (0,0) (0,2) (3,2) (3,0)    == False
esCuadrado (0,0) (3,4) (8,4) (5,0)    == False
esCuadrado (0,0) (0,0) (1,1) (0,0)    == False
esCuadrado (0,0) (0,0) (1,0) (0,1)    == False
esCuadrado (0,0) (1,0) (0,1) (-1,-1)  == False

Leer más…

Definir las funciones

noCuadrados :: [Integer]
graficaNoCuadrados :: Integer -> IO ()

tales que

• noCuadrados es la lista de los números naturales que no son cuadrados. Por ejemplo,

λ> take 25 noCuadrados
[2,3,5,6,7,8,10,11,12,13,14,15,17,18,19,20,21,22,23,24,26,27,28,29,30]

• (graficaNoCuadrados n) dibuja las diferencias entre los n primeros elementos de noCuadrados y sus posiciones. Por ejemplo, (graficaNoCuadrados 300) dibuja

(graficaNoCuadrados 3000) dibuja

(graficaNoCuadrados 30000) dibuja

Comprobar con QuickCheck que el término de noCuadrados en la posición n-1 es (n + floor(1/2 + sqrt(n))).

Leer más…

Un árbol binario completo es un árbol en el que cada nodo tiene cero o dos hijos. Por ejemplo, el primero de los siguientes árboles es un árbol binario completo pero los otros no lo son

     1              1            1
   /   \          /   \        / | \
  2     3        2     3      2  7  3
 / \            /            / \
4   5          4            4   5

Los árboles se pueden representar mediante el siguiente tipo de datos

data Arbol a = N a [Arbol a]
  deriving Show

Por ejemplo, los árboles los árboles anteriores se puede representar por

ej1, ej2, ej3 :: Arbol Int
ej1 = N 1 [N 2 [N 4 [], N 5 []], N 3 []]
ej2 = N 1 [N 2 [N 4 []], N 3 []]
ej3 = N 1 [N 2 [N 4 [], N 5 []], N 7 [], N 3 []]

Definir la función

esBinarioCompleto :: Arbol t -> Bool

tal que (esBinarioCompleto a) se verifica si a es un árbol binario completo. Por ejemplo,

esBinarioCompleto ej1  ==  True
esBinarioCompleto ej2  ==  False
esBinarioCompleto ej3  ==  False

Leer más…

Definir la función

menor :: Integer -> Integer

tal que (menor n) es el menor número divisible por 10^n cuyos dígitos suman n. Por ejemplo,

menor 5   ==  500000
menor 20  ==  29900000000000000000000

Leer más…

Un número trimórfico es un número cuyo cubo termina en dicho número. Por ejemplo, 24 es trimórfico ya que 24^3 = 13824 termina en 24.

Para cada entero positivo n, la densidad de trimórficos hasta n es el cociente entre la cantidad de números trimórficos menores o iguales que n y el número n. Por ejemplo, hasta 10 hay 6 números trimórficos (0, 1, 4, 5, 6 y 9); por tanto, la densidad hasta 10 es 6/10 = 0.6.

Definir las funciones

trimorficos         :: [Integer]
densidadTrimorficos :: Integer -> Double

tal que

• trimorficos es la lista de los números trimórficos. Por ejemplo,

λ> take 20 trimorficos
[0,1,4,5,6,9,24,25,49,51,75,76,99,125,249,251,375,376,499,501]

• (densidadTrimorficos n) es la densidad de trimórficos hasta n. Por ejemplo,

densidadTrimorficos 10      ==  0.6
densidadTrimorficos 100     ==  0.13
densidadTrimorficos 1000    ==  2.6e-2
densidadTrimorficos 10000   ==  3.7e-3
densidadTrimorficos 100000  ==  4.8e-4

Leer más…

Los primeros términos de la sucesión de Fibonacci son

0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610

Al calcular sus restos módulo 3 se obtiene

0,1,1,2,0,2,2,1, 0,1,1,2,0,2,2,1

Se observa que es periódica y su período es

0,1,1,2,0,2,2,1

Definir las funciones

fibsMod                   :: Integer -> [Integer]
periodoFibMod             :: Integer -> [Integer]
longPeriodosFibMod        :: [Int]
graficaLongPeriodosFibMod :: Int -> IO ()

tales que

• (fibsMod n) es la lista de los términos de la sucesión de Fibonacci módulo n. Por ejemplo,

λ> take 24 (fibsMod 3)
[0,1,1,2,0,2,2,1, 0,1,1,2,0,2,2,1, 0,1,1,2,0,2,2,1]
λ> take 24 (fibsMod 4)
[0,1,1,2,3,1, 0,1,1,2,3,1, 0,1,1,2,3,1, 0,1,1,2,3,1]

• (periodoFibMod n) es la parte perioica de la sucesión de Fibonacci módulo n. Por ejemplo,

periodoFibMod 3  ==  [0,1,1,2,0,2,2,1]
periodoFibMod 4  ==  [0,1,1,2,3,1]
periodoFibMod 7  ==  [0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1]

• longPeriodosFibMod es la sucesión de las longitudes de los períodos de las sucesiones de Fibonacci módulo n, para n > 0. Por ejemplo,

λ> take 20 longPeriodosFibMod
[1,3,8,6,20,24,16,12,24,60,10,24,28,48,40,24,36,24,18,60]

• (graficaLongPeriodosFibMod n) dibuja la gráfica de los n primeros términos de la sucesión longPeriodosFibMod. Por ejemplo, (graficaLongPeriodosFibMod n) dibuja

Leer más…