La sucesión de Lichtenberg esta formada por la representación decimal de los números binarios de la sucesión de dígitos 0 y 1 alternados. Los primeros términos de ambas sucesiones son

Alternada ..... Lichtenberg
0 ....................... 0
1 ....................... 1
10 ...................... 2
101 ..................... 5
1010 ................... 10
10101 .................. 21
101010 ................. 42
1010101 ................ 85
10101010 .............. 170
101010101 ............. 341
1010101010 ............ 682
10101010101 .......... 1365
101010101010 ......... 2730

Definir las funciones

lichtenberg        :: [Integer]
graficaLichtenberg :: Int -> IO ()

tales que

• lichtenberg es la lista cuyos elementos son los términos de la sucesión de Lichtenberg. Por ejemplo,

λ> take 17 lichtenberg
[0,1,2,5,10,21,42,85,170,341,682,1365,2730,5461,10922,21845,43690]

• (graficaLichtenberg n) dibuja la gráfica del número de dígitos de los n primeros términos de la sucesión de Lichtenberg. Por ejemlo, (graficaLichtenberg 100) dibuja

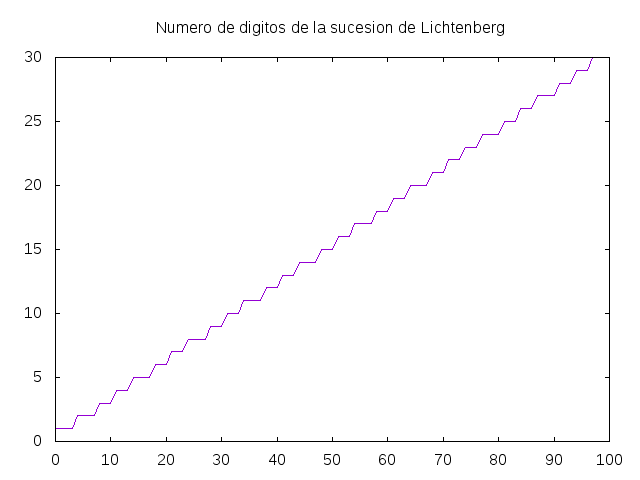
Comprobar con QuickCheck que todos los términos de la sucesión de Lichtenberg, a partir del 4º, son números compuestos.

Leer más…

Los primeros términos de la sucesión de los dígitos 0 y 1 alternados son

0
1
10
101
1010
10101
101010
1010101
10101010
101010101

Definir la lista

sucAlternada :: [Integer]

tal que sus elementos son los términos de la sucesión de los dígitos 0 y 1 alternados. Por ejemplo,

λ> take 10 sucAlternada
[0,1,10,101,1010,10101,101010,1010101,10101010,101010101]

Leer más…

En 1939 Dov Juzuk extendió el método de Nicómaco del cálculo de los cubos. La extensión se basaba en los siguientes pasos:

• se comienza con la lista de todos los enteros positivos

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ...

• se agrupan tomando el primer elemento, los dos siguientes, los tres siguientes, etc.

[[1], [2, 3], [4, 5, 6], [7, 8, 9, 10], [11, 12, 13, 14, 15], ...

• se seleccionan los elementos en posiciones pares

[[1],         [4, 5, 6],                [11, 12, 13, 14, 15], ...

• se suman los elementos de cada grupo

[1,           15,                       65,                   ...

• se calculan las sumas acumuladas

[1,           16,                       81,                   ...

Las sumas obtenidas son las cuantas potencias de los números enteros positivos.

Definir las funciones

listasParcialesJuzuk :: [a] -> [[a]]
sumasParcialesJuzuk  :: [Integer] -> [Integer]

tal que

• (listasParcialesJuzuk xs) es lalista de ls listas parciales de Juzuk; es decir, la selección de los elementos en posiciones pares de la agrupación de los elementos de xs tomando el primer elemento, los dos siguientes, los tres siguientes, etc. Por ejemplo,

λ> take 4 (listasParcialesJuzuk [1..])
[[1],[4,5,6],[11,12,13,14,15],[22,23,24,25,26,27,28]]
λ> take 4 (listasParcialesJuzuk [1,3..])
[[1],[7,9,11],[21,23,25,27,29],[43,45,47,49,51,53,55]]

• (sumasParcialesJuzuk xs) es la lista de las sumas acumuladas de los elementos de las listas de Juzuk generadas por xs. Por ejemplo,

take 4 (sumasParcialesJuzuk [1..])  ==  [1,16,81,256]
take 4 (sumasParcialesJuzuk [1,3..])  ==  [1,28,153,496]

Comprobar con QuickChek que, para todo entero positivo n,

• el elemento de (sumasParcialesJuzuk [1..]) en la posición (n-1) es n^4.
• el elemento de (sumasParcialesJuzuk [1,3..]) en la posición (n-1) es n^2*(2*n^2 - 1).
• el elemento de (sumasParcialesJuzuk [1,5..]) en la posición (n-1) es 4*n^4-3*n^2.
• el elemento de (sumasParcialesJuzuk [2,3..]) en la posición (n-1) es n^2*(n^2+1).

Leer más…

El complemento potencial de un número entero positivo x es el menor número y tal que el producto de x por y es un una potencia perfecta. Por ejemplo,

• el complemento potencial de 12 es 3 ya que 12 y 24 no son potencias perfectas pero 36 sí lo es;
• el complemento potencial de 54 es 4 ya que 54, 108 y 162 no son potencias perfectas pero 216 = 6^3 sí lo es.

Definir las funciones

complemento                 :: Integer -> Integer
graficaComplementoPotencial :: Integer -> IO ()

tales que

• (complemento x) es el complemento potencial de x; por ejemplo,

complemento 12     ==  3
complemento 54     ==  4
complemento 720    ==  5
complemento 24000  ==  9
complemento 2018   ==  2018

• (graficaComplementoPotencial n) dibuja la gráfica de los complementos potenciales de los n primeros números enteros positivos. Por ejemplo, (graficaComplementoPotencial 100) dibuja

y (graficaComplementoPotencial 500) dibuja

Comprobar con QuickCheck que (complemento x) es menor o igual que x.

Leer más…

Una terna pitagórica con primer lado x es una terna (x,y,z) tal que x^2 + y^2 = z^2. Por ejemplo, las ternas pitagóricas con primer lado 16 son (16,12,20), (16,30,34) y (16,63,65).

Definir las funciones

ternasPitagoricas      :: Integer -> [(Integer,Integer,Integer)]
mayorTernaPitagorica   :: Integer -> (Integer,Integer,Integer)
graficaMayorHipotenusa :: Integer -> IO ()

tales que

• (ternasPitgoricas x) es la lista de las ternas pitagóricas con primer lado x. Por ejemplo,

ternasPitagoricas 16 == [(16,12,20),(16,30,34),(16,63,65)]
ternasPitagoricas 20 == [(20,15,25),(20,21,29),(20,48,52),(20,99,101)]
ternasPitagoricas 25 == [(25,60,65),(25,312,313)]
ternasPitagoricas 26 == [(26,168,170)]

• (mayorTernaPitagorica x) es la mayor de las ternas pitagóricas con primer lado x. Por ejemplo,

mayorTernaPitagorica 16     ==  (16,63,65)
mayorTernaPitagorica 20     ==  (20,99,101)
mayorTernaPitagorica 25     ==  (25,312,313)
mayorTernaPitagorica 26     ==  (26,168,170)
mayorTernaPitagorica3 2018  ==  (2018,1018080,1018082)
mayorTernaPitagorica3 2019  ==  (2019,2038180,2038181)

• (graficaMayorHipotenusa n) dibuja la gráfica de las sucesión de las mayores hipotenusas de las ternas pitagóricas con primer lado x, para x entre 3 y n. Por ejemplo, (graficaMayorHipotenusa 100) dibuja

Leer más…

Este ejercicio está basado en el artículo La conjetura de la "escalada hasta un primo" publicado esta semana por Miguel Ángel Morales en su blog Gaussianos.

La conjetura de escalada hasta un primo, propuesta por John Horton Conway, es sencilla de plantear, pero primero vamos a ver qué es eso de escalar hasta un primo. Tomamos un número cualquiera y lo descomponemos en factores primos (colocados en orden ascendente). Si el número era primo, ya hemos acabado; si no era primo, construimos el número formado por los factores primos y los exponentes de los mismos colocados tal cual salen en la factorización. Con el número obtenido hacemos lo mismo que antes. La escalada finaliza cuando obtengamos un número primo. Por ejemplo, para obtener la escalada prima de 1400, como no es primo, se factoriza (obteniéndose 2^3 * 5^2 * 7) y se unen bases y exponentes (obteniéndose 23527). Con el 23527 se repite el proceso obteniéndose la factorización (7 * 3361) y su unión (73361). Como el 73361 es primo, termina la escalada. Por tanto, la escalada de 1400 es [1400,23527,73361].

La conjetura de Conway sobre "escalada hasta un primo" dice que todo número natural mayor o igual que 2 termina su escalada en un número primo.

Definir las funciones

escaladaPrima                :: Integer -> [Integer]
longitudEscaladaPrima        :: Integer -> Integer
longitudEscaladaPrimaAcotada :: Integer -> Integer -> Integer
graficaEscalada              :: Integer -> Integer -> IO ()

tales que

• (escaladaPrima n) es la escalada prima de n. Por ejemplo,

λ> escaladaPrima 1400
[1400,23527,73361]
λ> escaladaPrima 333
[333,3237,31383,3211317,3217139151,39722974813]
λ> take 10 (escaladaPrima 20)
[20,225,3252,223271,297699,399233,715623,3263907,32347303,160720129]
λ> take 3 (escaladaPrima 13532385396179)
[13532385396179,13532385396179,13532385396179]
λ> take 2 (escaladaPrima 45214884853168941713016664887087462487)
[45214884853168941713016664887087462487,13532385396179]

• (longitudEscaladaPrima n) es la longitud de la escalada prima de n. Por ejemplo,

longitudEscaladaPrima 1400  ==  3
longitudEscaladaPrima 333   ==  6

• (longitudEscaladaPrimaAcotada n k) es el mínimo entre la longitud de la escalada prima de n y k. Por ejemplo,

longitudEscaladaPrimaAcotada 333 10  ==  6
longitudEscaladaPrimaAcotada 333 4   ==  4
longitudEscaladaPrimaAcotada 20 4    ==  4

• (graficaEscalada n k) dibuja la gráfica de (longitudEscaladaPrimaAcotada x k) para x entre 2 y n. Por ejemplo, (graficaEscalada 120 15) dibuja

Leer más…

El número 45 se puede escribir de tres formas como diferencia de los cuadrados de dos números naturales:

45 =  7^2 -  2^2
   =  9^2 -  6^2
   = 23^2 - 22^2

Definir la función

   diferencias :: Integer -> Integer -> [(Integer,Integer)]

tal que (diferencias x n) es la lista de pares tales que la diferencia de sus potencias n-ésima es x. Por ejemplo,

   diferencias 45 2    ==  [(7,2),(9,6),(23,22)]
   diferencias 50 2    ==  []
   diferencias 19 3    ==  [(3,2)]
   diferencias 8 3     ==  [(2,0)]
   diferencias 15 4    ==  [(2,1)]
   diferencias 4035 2  ==  [(142,127),(406,401),(674,671),(2018,2017)]
   head (diferencias 1161480105172255454401 5)  ==  (123456,123455)

Leer más…

Escribir, usando CodeWorld, un programa para dibujar el fractal hexagonal que se muestra en la siguiente animación

Las 5 fases de la animación son

• Fase 0:
• Fase 1:
• Fase 2:
• Fase 3:
• Fase 4:

Leer más…

Nicómaco de Gerasa vivió en Palestina entre los siglos I y II de nuestra era. Escribió Arithmetike eisagoge (Introducción a la aritmética) que es el primer trabajo en donde se trata la Aritmética de forma separada a la Geometría. En el tratado se encuentra la siguiente proposición: "si se escriben los números impares

1, 3, 5, 7, 9, 11, 13, 15, 17, ...

entonces el primero es el cubo de 1; la suma de los dos siguientes, el cubo de 2; la suma de los tres siguientes, el cubo de 3; y así sucesivamente."

Definir las siguientes funciones

listasParciales :: [a] -> [[a]]
sumasParciales  :: [Int] -> [Int]

tales que

• (listasParciales xs) es la lista obtenido agrupando los elementos de la lista infinita xs de forma que la primera tiene 0 elementos; la segunda, el primer elemento de xs; la tercera, los dos siguientes; y así sucesivamente. Por ejemplo,

λ> take 7 (listasParciales [1..])
[[],[1],[2,3],[4,5,6],[7,8,9,10],[11,12,13,14,15],[16,17,18,19,20,21]]
λ> take 7 (listasParciales [1,3..])
[[],[1],[3,5],[7,9,11],[13,15,17,19],[21,23,25,27,29],[31,33,35,37,39,41]]

• (sumasParciales xs) es la lista de las sumas parciales de la lista infinita xs. Por ejemplo,

λ> take 15 (sumasParciales [1..])
[0,1,5,15,34,65,111,175,260,369,505,671,870,1105,1379]
λ> take 15 (sumasParciales [1,3..])
[0,1,8,27,64,125,216,343,512,729,1000,1331,1728,2197,2744]

Comprobar con QuickChek la propiedad de Nicómaco; es decir, que para todo número natural n, el término n-ésimo de (sumasParciales [1,3..]) es el cubo de n.

Leer más…

Un número malvado es un número natural cuya expresión en base 2 (binaria) contiene un número par de unos.

Un número odioso es un número natural cuya expresión en base 2 (binaria) contiene un número impar de unos.

Podemos representar los números malvados y odiosos mediante el siguiente tipo de dato

data MalvadoOdioso = Malvado | Odioso deriving Show

Definir la función

malvadoOdioso :: Integer -> MalvadoOdioso

tal que (malvadoOdioso n) devuelve el tipo de número que es n. Por ejemplo,

λ> malvadoOdioso 11
Odioso
λ> malvadoOdioso 12
Malvado
λ> malvadoOdioso3 (10^20000000)
Odioso
λ> malvadoOdioso3 (1+10^20000000)
Malvado

Leer más…