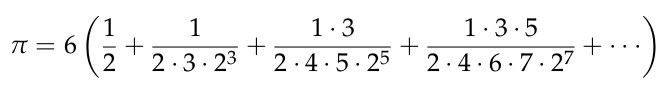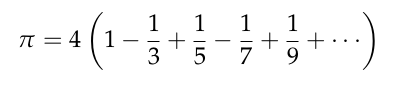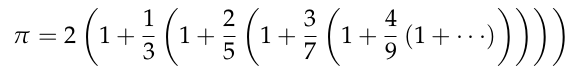Misceláneas

Al permutar los elementos de la lista [1,2,3,4] se obtienen los siguientes valores de la suma de pares de elementos consecutivos:

10, por ejemplo con [1,4,2,3] ya que 1x4+2x3 = 10
11, por ejemplo con [1,3,2,4] ya que 1x3+2x4 = 11
14, por ejemplo con [1,2,3,4] ya que 1x2+3x4 = 14

Por tanto, la mínima suma de los productos de elementos consecutivos en las permutaciones de [1,2,3,4] es 10 y una permutación con dicha suma es [1,4,2,3].

Definir las funciones

minimaSumaProductos  :: (Num a, Ord a) => [a] -> a
permutacionMinimal   :: (Num a, Ord a) => [a] -> [a]

tales que

(minimaSumaProductos xs) es la mínima suma de los productos de elementos consecutivos en las permutaciones de lista xs, suponiendo que xs tiene un número par de elementos. Por ejemplo,

minimaSumaProductos [1..4]             ==  10
minimaSumaProductos [3,2,5,7,1,6]      ==  34
minimaSumaProductos [9,2,8,4,5,7,6,0]  ==  74
minimaSumaProductos [1,2,1,4,0,5,6,0]  ==  6

(permutacionMinimal xs) es una permutación de xs cuya suma de productos de elementos consecutivos de xs es la mínima suma de los productos de elementos consecutivos en las permutaciones de lista xs, suponiendo que xs tiene un número par de elementos. Por ejemplo,

permutacionMinimal [1..4]             ==  [1,4,3,2]
permutacionMinimal [3,2,5,7,1,6]      ==  [1,7,2,6,3,5]
permutacionMinimal [9,2,8,4,5,7,6,0]  ==  [0,9,2,8,4,7,5,6]
permutacionMinimal [1,2,1,4,0,5,6,0]  ==  [0,6,0,5,1,4,1,2]

Máxima potencia que divide al factorial

José A. Alonso

26-01-2017

Misceláneas

La máxima potencia de 2 que divide al factorial de 5 es 3, ya que 5! = 120, 120 es divisible por 2^3 y no lo es por 2^4.

Definir la función

maxPotDivFact :: Integer -> Integer -> Integer

tal que (maxPotDivFact p n), para cada primo p, es el mayor k tal que p^k divide al factorial de n. Por ejemplo,

maxPotDivFact 2 5       ==  3
maxPotDivFact 3 6       ==  2
maxPotDivFact 2 10      ==  8
maxPotDivFact 3 10      ==  4
maxPotDivFact 2 (10^2)  ==  97
maxPotDivFact 2 (10^3)  ==  994
maxPotDivFact 2 (10^4)  ==  9995
maxPotDivFact 2 (10^5)  ==  99994
maxPotDivFact 2 (10^6)  ==  999993
maxPotDivFact 3 (10^5)  ==  49995
maxPotDivFact 3 (10^6)  ==  499993
maxPotDivFact 7 (10^5)  ==  16662
maxPotDivFact 7 (10^6)  ==  166664
length (show (maxPotDivFact 2 (10^20000)))  ==  20000

Árboles continuos

José A. Alonso

25-01-2017

Misceláneas

Los árboles binarios se pueden representar con el de tipo de dato algebraico

data Arbol a = H
             | N a (Arbol a) (Arbol a)
  deriving Show

Por ejemplo, los árboles

    3                7
   / \              / \
  2   4            5   8
 / \   \          / \   \
1   3   5        6   4   10

se representan por

ej1, ej2 :: Arbol Int
ej1 = N 3 (N 2 (N 1 H H) (N 3 H H)) (N 4 H (N 5 H H))
ej2 = N 7 (N 5 (N 6 H H) (N 4 H H)) (N 8 H (N 10 H H))

Un árbol binario es continuo si el valor absoluto de la diferencia de los elementos adyacentes es 1. Por ejemplo, el árbol ej1 es continuo ya que el valor absoluto de sus pares de elementos adyacentes son

|3-2| = |2-1| = |2-3| = |3-4| = |4-5| = 1

En cambio, el ej2 no lo es ya que |8-10| ≠ 1.

Definir la función

esContinuo :: (Num a, Eq a) => Arbol a -> Bool

tal que (esContinuo x) se verifica si el árbol x es continuo. Por ejemplo,

esContinuo ej1  ==  True
esContinuo ej2  ==  False

La sucesión "Mira y di"

José A. Alonso

24-01-2017

Misceláneas

La sucesión "Mira y di" (en inglés, Look-and-Say) es una sucesión de números naturales en donde cada término se obtiene agrupando las cifras iguales del anterior y recitándolas. Por ejemplo, si x(0) = 1 se lee como "un uno" y por tanto x(1) = 11. Análogamente,

x(1) = 11     (dos unos                          --> 21)
x(2) = 21     (un dos un uno                     --> 1211)
x(3) = 1211   (un uno un dos dos unos            --> 111221)
x(4) = 111221 (tres unos dos doses un uno        --> 312211)
x(5) = 312211 (un tres un uno dos doses dos unos --> 13112221)

Definir la función

sucMiraYDi :: Integer -> [Integer]

tal que (sucMiraYDi n) es la sucesión "Mira y di" cuyo primer término es n. Por ejemplo,

λ> take 9 (sucMiraYdi 1)
[1,11,21,1211,111221,312211,13112221,1113213211,31131211131221]
λ> take 5 (sucMiraYdi 2017)
[2017,12101117,111211103117,31123110132117,1321121321101113122117]
λ> take 7 (sucMiraYDi 22)
[22,22,22,22,22,22,22]
λ> (sucMiraYDi 1) !! 11
3113112221232112111312211312113211
λ> (sucMiraYDi 1) !! 12
1321132132111213122112311311222113111221131221

Independientemente del término inicial x(0) elegido (con la única salvedad del 22), la sucesión diverge y la razón entre el número de cifras de x(n) y el de x(n-1) tiende a un valor fijo que es la constante de Conway λ ≈ 1.303577269. Por ejemplo, para x(0) = 1, las razones son

2, 1, 2, 1.5, 1, 1.3333333333333333, 1.25, 1.4, 1.4285714285714286, 1.3

Definir la función

aproximacionConway :: Integer -> Double -> Int

tal que (aproximacionConway n e) es el menor k tal que la diferencia entre la constante de Conway y la razón entre el número de cifras de x(k) x(k-1) es, en valor absoluto, menor que e. Por ejemplo,

aproximacionConway 1 0.3     ==  3
aproximacionConway 1 0.1     ==  5
aproximacionConway 1 0.01    ==  9
aproximacionConway 1 0.001   ==  24
aproximacionConway 1 0.0001  ==  43
aproximacionConway 2 0.0001  ==  47

Cadena de primos

José A. Alonso

23-01-2017

Misceláneas

La lista de los primeros números primos es

[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71]

Los primeros elementos de la cadena obtenida concatenado los números primos es

"23571113171923293137414347535961677173798389971011"

Definir la función

primoEnPosicion :: Int -> Integer

tal que (primoEnPosicion n) es el número primo que tiene algún dígito en la posición n de la cadena obtenida concatenado los números primos. Por ejemplo,

primoEnPosicion 0       ==  2
primoEnPosicion 1       ==  3
primoEnPosicion 4       ==  11
primoEnPosicion 5       ==  11
primoEnPosicion 6       ==  13
primoEnPosicion 1022    ==  2011
primoEnPosicion 1023    ==  2017
primoEnPosicion 1026    ==  2017
primoEnPosicion 1027    ==  2027
primoEnPosicion (10^7)  ==  21242357

Notación polaca inversa

José A. Alonso

20-01-2017

Misceláneas

La notación polaca inversa (en inglés, Reverse Polish Notation, o RPN), es una forma alternativa de escribir expresiones matemáticas. Por ejemplo, la expresión "20 - (4 + 3) * 2" en RPN es "20 4 3 + 2 * -".

Para evaluar una expresión en RPN, usamos una lista auxiliar (inicialmente vacía) y recorremos la expresión de izquierda a derecha. Cada vez que encontramos un número, lo añadimos a la lista auxiliar. Cuando encontramos un operador, retiramos los dos números que hay al principio de la pila, utilizamos el operador con ellos y los quitamos de la lista y le añadimos el resultado. Cuando alcancemos el final de la expresión, debemos tener un solo número en la lista auxiliar si la expresión estaba bien formada, y éste representa el resultado de la expresión. Por ejemplo, la evaluación de RPN "20 4 3 + 2 * -" es la siguiente

""                 []
"20"               [20]
"20 4"             [4, 20]
"20 4 3"           [3, 4, 20]
"20 4 3 +"         [7, 20]
"20 4 3 + 2"       [2, 7, 20]
"20 4 3 + 2 *"     [14, 20]
"20 4 3 + 2 * -"   [6]

Definir la función

valor :: String -> Float

tal que (valor cs) es el valor de la expresión RPN cs. Por ejemplo,

valor "4"               ==  4.0
valor "4 3 +"           ==  7.0
valor "4 3 + 2 *"       ==  14.0
valor "20 4 3 + 2 * -"  ==  6.0
valor "3 7 + 2 /"       ==  5.0

La conjetura de Rodolfo

José A. Alonso

19-01-2017

Misceláneas

El pasado 1 de enero, Claudio Meller publicó el artículo La conjetura de Rodolfo que afirma que

Todos los números naturales se pueden números pueden expresarse como la suma de un capicúa y un capicúa especial (siendo los capicúas especiales los números que al quitarles los ceros finales son capicúas; por ejemplo, 32300, 50500 y 78987).

Definir las funciones

descomposiciones               :: Integer -> [(Integer, Integer)]
contraejemplosConjeturaRodolfo :: [Integer]

tales que

(descomposiciones x) es la lista de las descomposiciones de x como la suma de un capicúa y un capicúa especial. Por ejemplo,

descomposiciones 1980  ==  [(99,1881),(979,1001)]
descomposiciones 2016  ==  [(575,1441),(606,1410)]
descomposiciones 1971  ==  [(161,1810),(1771,200),(1881,90)]

contraejemplosConjeturaRodolfo es la lista de contraejemplos de la conjetura de Rodolfo; es decir, de los números que no pueden expresarse com la suma de un capicúa y un capicúa especial. Por ejemplo,

λ> take 12 contraejemplosConjeturaRodolfo
[1200,1220,1240,1250,1260,1270,1280,1290,1300,1330,1350,1360]
λ> take 12 (dropWhile (< 2000) contraejemplosConjeturaRodolfo)
[3020,3240,3350,3460,3570,3680,3920,4030,4250,4360,4470,4580]

Sustitución en una posición

José A. Alonso

18-01-2017

Misceláneas

Los árboles binarios se pueden representar con el de dato algebraico

data Arbol a = H
             | N a (Arbol a) (Arbol a)
             deriving Show

Por ejemplo, los árboles

     9                9
    / \              /
   /   \            /
  8     6          8
 / \   / \        / \
3   2 4   5      3   2

se pueden representar por

ej1, ej2:: Arbol Int
ej1 = N 9 (N 8 (N 3 H H) (N 2 H H)) (N 6 (N 4 H H) (N 5 H H))
ej2 = N 9 (N 8 (N 3 H H) (N 2 H H)) H

Para indicar las posiciones del árbol se define el tipo

type Posicion = [Direccion]

donde

data Direccion = D | I
  deriving Eq

representa un movimiento hacia la derecha (D) o a la izquierda. Por ejemplo, las posiciones de los elementos del ej1 son

9 []
8 [I]
3 [I,I]
2 [I,D]
6 [D]
4 [D,I]
5 [D,D]

Definir la función

sustitucion :: Posicion -> a -> Arbol a -> Arbol a

tal que (sustitucion ds z x) es el árbol obtenido sustituyendo el elemento de x en la posición ds por z. Por ejemplo,

λ> sustitucion [I,D] 7 ej1
N 9 (N 8 (N 3 H H) (N 7 H H)) (N 6 (N 4 H H) (N 5 H H))
λ> sustitucion [D,D] 7 ej1
N 9 (N 8 (N 3 H H) (N 2 H H)) (N 6 (N 4 H H) (N 7 H H))
λ> sustitucion [I] 7 ej1
N 9 (N 7 (N 3 H H) (N 2 H H)) (N 6 (N 4 H H) (N 5 H H))
λ> sustitucion [] 7 ej1
N 7 (N 8 (N 3 H H) (N 2 H H)) (N 6 (N 4 H H) (N 5 H H))

Sumas de dos capicúas

José A. Alonso

17-01-2017

Misceláneas

Definir las funciones

sumas2Capicuas  :: Integer -> [(Integer, Integer)]
noSuma2Capicuas :: [Integer]

tales que

(sumas2Capicuas x) es la lista de las descomposiciones de x como suma de dos capicúas (con el primer sumando menor o igual que el segundo). Por ejemplo,

sumas2Capicuas 17  == [(6,11),(8,9)]
sumas2Capicuas 187 == [(6,181),(66,121),(88,99)]
sumas2Capicuas 165 == [(4,161),(44,121),(66,99),(77,88)]
sumas2Capicuas 382 == [(9,373),(191,191)]
sumas2Capicuas 151 == [(0,151)]
sumas2Capicuas 201 == []

noSuma2Capicuas es la sucesión de los números que no se pueden escribir como suma de dos capicúas. Por ejemplo,

λ> take 15 noSuma2Capicuas
[21,32,43,54,65,76,87,98,201,1031,1041,1042,1051,1052,1053]
λ> noSuma2Capicuas !! 3000
19941

Inversa del factorial

José A. Alonso

16-01-2017

Misceláneas

Definir la función

inversaFactorial :: Integer -> Maybe Integer

tal que (inversaFactorial x) es (Just n) si el factorial de n es x y es Nothing si no existe ningún número n tal que el factorial de n es x. Por ejemplo,

inversaFactorial 24  ==  Just 4
inversaFactorial 25  ==  Nothing

Suma ordenada de listas infinitas ordenadas

José A. Alonso

13-01-2017

Misceláneas

Definir la función

sumaOrdenada :: [Integer] -> [Integer] -> [Integer]

tal que (sumaOrdenada xs ys) es la suma ordenada de las listas infinitas crecientes xs e ys. Por ejemplo,

λ> take 15 (sumaOrdenada [5,10..] [7,14..])
[12,17,19,22,24,26,27,29,31,32,33,34,36,37,38]
λ> take 15 (sumaOrdenada [2^n | n <- [0..]] [3^n | n <- [0..]])
[2,3,4,5,7,9,10,11,13,17,19,25,28,29,31]

Sumas de tres capicúas

José A. Alonso

12-01-2017

Misceláneas

Definir la función

sumas3Capicuas  :: Integer -> [(Integer, Integer, Integer)]

tales que (sumas3Capicuas x) es la lista de las descomposiciones de x como suma de tres capicúas (con los sumandos no decrecientes). Por ejemplo,

sumas3Capicuas 0  ==  [(0,0,0)]
sumas3Capicuas 1  ==  [(0,0,1)]
sumas3Capicuas 2  ==  [(0,0,2),(0,1,1)]
sumas3Capicuas 3  ==  [(0,0,3),(0,1,2),(1,1,1)]
sumas3Capicuas 4  ==  [(0,0,4),(0,1,3),(0,2,2),(1,1,2)]
length (sumas3Capicuas 17)      ==  17
length (sumas3Capicuas 2017)    ==  47
length (sumas3Capicuas 999999)  ==  15266

Comprobar con QuickCheck que todo número natural se puede escribir como suma de tres capicúas.

Sucesión de capicúas

José A. Alonso

11-01-2017

Misceláneas

Definir las funciones

capicuas        :: [Integer]
posicionCapicua :: Integer -> Integer

tales que

capicuas es la sucesión de los números capicúas. Por ejemplo,

λ> take 45 capicuas
[0,1,2,3,4,5,6,7,8,9,11,22,33,44,55,66,77,88,99,101,111,121,131,
 141,151,161,171,181,191,202,212,222,232,242,252,262,272,282,292,
 303,313,323,333,343,353]
λ> capicuas !! (10^5)
900010009

(posicionCapicua x) es la posición del número capicúa x en la sucesión de los capicúas. Por ejemplo,

λ> posicionCapicua 353
44
λ> posicionCapicua 900010009
100000
λ> let xs = show (123^30)
λ> posicionCapicua (read (xs ++ reverse xs))
1497912859868342793044999075260564303046944727069807798026337448
λ> posicionCapicua (read (xs ++ "7" ++ reverse xs))
5979128598683427930449990752605643030469447270698077980263374496

Nodos con k sucesores

José A. Alonso

10-01-2017

Misceláneas

Sumas y restas alternativas

José A. Alonso

09-01-2017

Misceláneas

Definir la función

sumasYrestas :: Num a => [a] -> a

tal que (sumasYrestas xs) es el resultado de alternativamente los elementos de xs. Por ejemplo,

sumasYrestas [3,2,4,1,7] = 3 - 2 + 4 - 1 + 7
                         = 11

Otros ejemplos,

sumasYrestas [3,2,4]              ==  5
sumasYrestas [3,2,4,1]            ==  4
sumasYrestas [3,2,4,1,7]          ==  11
sumasYrestas (replicate (10^6) 1) ==  0

Números dorados

José A. Alonso

06-01-2017

Misceláneas

Los dígitos del número 2375 se pueden separar en dos grupos de igual tamaño ([7,2] y [5,3]) tales que para los correspondientes números (72 y 53) se verifique que la diferencia de sus cuadrados sea el número original (es decir, 72^2 - 53^2 = 2375).

Un número x es dorado si sus dígitos se pueden separar en dos grupos de igual tamaño tales que para los correspondientes números (a y b) se verifique que la diferencia de sus cuadrados sea el número original (es decir, b^2 - a^2 = x).

Definir la función

esDorado :: Integer -> Bool

tales que (esDorado x) se verifica si x es un número dorado. Por ejemplo,

λ> esDorado 2375
True
λ> take 5 [x | x <- [1..], esDorado x]
[48,1023,1404,2325,2375]

Sucesión de cuadrados reducidos

José A. Alonso

05-01-2017

Misceláneas

La sucesión de cuadrados de orden n definida a partir de un número x se forma iniciándola en x y, para cada término z el siguiente es el número formado por los n primeros dígitos del cuadrado de z. Por ejemplo, para n = 4 y x = 1111, el primer término de la sucesión es 1111, el segundo es 1234 (ya que 1111^2 = 1234321) y el tercero es 1522 (ya que 1234^2 = 1522756).

Definir la función

sucCuadrados :: Int -> Integer -> [Integer]

tal que (sucCuadrados n x) es la sucesión de cuadrados de orden n definida a partir de x. Por ejemplo,

λ> take 10 (sucCuadrados 4 1111)
[1111,1234,1522,2316,5363,2876,8271,6840,4678,2188]
λ> take 10 (sucCuadrados 3 457)
[457,208,432,186,345,119,141,198,392,153]
λ> take 20 (sucCuadrados 2 55)
[55,30,90,81,65,42,17,28,78,60,36,12,14,19,36,12,14,19,36,12]

Familias de números con algún dígito en común

José A. Alonso

04-01-2017

Misceláneas

Una familia de números es una lista de números tal que todos tienen la misma cantidad de dígitos y, además, dichos números tienen al menos un dígito común.

Por ejemplo, los números 72, 32, 25 y 22 pertenecen a la misma familia ya que son números de dos dígitos y todos tienen el dígito 2, mientras que los números 123, 245 y 568 no pertenecen a la misma familia, ya que no hay un dígito que aparezca en los tres números.

Definir la función

esFamilia :: [Integer] -> Bool

tal que (esFamilia ns) se verifica si ns es una familia de números. Por ejemplo,

esFamilia [72, 32, 25, 22]  ==  True
esFamilia [123,245,568]     ==  False
esFamilia [72, 32, 25, 223] ==  False

Estratificación de un árbol

José A. Alonso

03-01-2017

Misceláneas

Los árboles se pueden representar mediante el siguiente tipo de datos

data Arbol a = N a [Arbol a]
  deriving Show

Por ejemplo, los árboles

  1         1             1
 / \       / \           / \
8   3     8   3         8   3
    |        /|\       /|\  |
    4       4 5 6     4 5 6 7

se representan por

ej1, ej2, ej3 :: Arbol Int
ej1 = N 1 [N 8 [],N 3 [N 4 []]]
ej2 = N 1 [N 8 [], N 3 [N 4 [], N 5 [], N 6 []]]
ej3 = N 1 [N 8 [N 4 [], N 5 [], N 6 []], N 3 [N 7 []]]

Un estrato de un árbol es la lista de nodos que se encuentran al mismo nivel de profundidad. Por ejemplo, los estratos del árbol ej1 son [1], [8,3] y [4].

Definir la función

estratos :: Arbol a -> [[a]]

tal que (estratos x) es la lista de los estratos del árbol x. Por ejemplo,

estratos ej1 == [[1],[8,3],[4]]
estratos ej2 == [[1],[8,3],[4,5,6]]
estratos ej3 == [[1],[8,3],[4,5,6,7]]

Terminaciones de Fibonacci

José A. Alonso

02-01-2017

Misceláneas

Definir la sucesión

sucFinalesFib :: [(Integer,Integer)]

cuyos elementos son los pares (n,x), donde x es el n-ésimo término de la sucesión de Fibonacci, tales que la terminación de x es n. Por ejemplo,

λ> take 6 sucFinalesFib
[(0,0),(1,1),(5,5),(25,75025),(29,514229),(41,165580141)]
λ> head [(n,x) | (n,x) <- sucFinalesFib, n > 200]
(245,712011255569818855923257924200496343807632829750245)
λ> head [n | (n,_) <- sucFinalesFib, n > 10^4]
10945

Segmentos comunes maximales

José A. Alonso

30-12-2016

Misceláneas

Los segmentos de de "abcd" son

["","a","ab","abc","abcd","b","bc","bcd","c","cd","d"]

Los segmentos comunes de "abcd" y "axbce" son

["","a","b","bc","c"]

Los segmentos comunes maximales de "abcd" y "axbce" son

["a","bc"]

Definir la función

segmentosComunesMaximales :: Eq a => [a] -> [a] -> [[a]]

tal que (segmentosComunesMaximales xs ys) es la lista de los segmentos comunes maximales de xs e ys. Por ejemplo,

segmentosComunesMaximales "abcd" "axbce"  ==  ["a","bc"]

Números de Perrin

José A. Alonso

29-12-2016

Misceláneas

Los números de Perrin se definen por la relación de recurrencia

P(n) = P(n - 2) + P(n - 3) si n > 2,

con los valores iniciales

P(0) = 3, P(1) = 0 y P(2) = 2.

Definir la sucesión

sucPerrin :: [Integer]

cuyos elementos son los números de Perrin. Por ejemplo,

λ> take 15 sucPerrin
[3,0,2,3,2,5,5,7,10,12,17,22,29,39,51]
λ> length (show (sucPerrin !! (2*10^5)))
24425

Comprobar con QuickCheck si se verifica la siguiente propiedad: para todo entero n > 1, el n-ésimo término de la sucesión de Perrin es divisible por n si y sólo si n es primo.

Mínima suma de las ramas de un árbol

José A. Alonso

28-12-2016

Misceláneas

Los árboles se pueden representar mediante el siguiente tipo de datos

data Arbol a = N a [Arbol a]
  deriving Show

Por ejemplo, los árboles

  1         1             1
 / \       / \           / \
8   3     5   3         5   3
    |        /|\       /|\  |
    4       4 7 6     4 7 6 7

se representan por

ej1, ej2, ej3 :: Arbol Int
ej1 = N 1 [N 8 [],N 3 [N 4 []]]
ej2 = N 1 [N 5 [], N 3 [N 4 [], N 7 [], N 6 []]]
ej3 = N 1 [N 5 [N 4 [], N 7 [], N 6 []], N 3 [N 7 []]]

Definir la función

minimaSuma :: Arbol Int -> Int

tal que (minimaSuma a) es el mínimo de las sumas de las ramas del árbol a. Por ejemplo,

minimaSuma ej1  ==  8
minimaSuma ej2  ==  6
minimaSuma ej3  ==  10

Números super pandigitales

José A. Alonso

27-12-2016

Misceláneas

Un entero positivo n es pandigital en base b si su expresión en base b contiene todos los dígitos de 0 a b-1 al menos una vez. Por ejemplo,

el 2 es pandigital en base 2 porque 2 en base 2 es 10,
el 11 es pandigital en base 3 porque 11 en base 3 es 102 y
el 75 es pandigital en base 4 porque 75 en base 4 es 1023.

Un número n es super pandigital de orden m si es pandigital en todas las bases desde 2 hasta m. Por ejemplo, 978 es super pandigital de orden 5 pues

en base 2 es: 1111010010
en base 3 es: 1100020
en base 4 es: 33102
en base 5 es: 12403

Definir la función

superPandigitales :: Integer -> [Integer]

tal que (superPandigitales m) es la lista de los números super pandigitales de orden m. Por ejemplo,

take 3 (superPandigitales 3) == [11,19,21]
take 3 (superPandigitales 4) == [75,99,114]
take 3 (superPandigitales 5) == [978,1070,1138]

Ternas coprimas

José A. Alonso

26-12-2016

Misceláneas

Definir la lista

ternasCoprimas :: [(Integer,Integer,Integer)]

cuyos elementos son ternas de primos relativos (a,b,c) tales que a < b y a + b == c. Por ejemplo,

λ> take 7 ternasCoprimas
[(1,2,3),(1,3,4),(2,3,5),(1,4,5),(3,4,7),(1,5,6),(2,5,7)]
λ> ternasCoprimas !! 300000
(830,993,1823)

Listas duplicadas

José A. Alonso

23-12-2016

Misceláneas

Se observa que en la cadena "aabbccddeffgg" todos los caracteres están duplicados excepto el 'e'. Al añadirlo obtenemos la lista "aabbccddeeffgg" y se dice que esta última está duplicada.

También se observa que "aaaabbbccccdd" no está duplicada (porque hay un número impar de 'b' consecutivas). Añadiendo una 'b' se obtiene "aaaabbbbccccdd" que está duplicada.

Definir las funciones

esDuplicada :: Eq a => [a] -> Bool
duplica     :: Eq a => [a] -> [a]

tales que

(esDuplicada xs) se verifica si xs es una lista duplicada. Por ejemplo,

esDuplicada "aabbccddeffgg"   ==  False
esDuplicada "aabbccddeeffgg"  ==  True
esDuplicada "aaaabbbccccdd"   ==  False
esDuplicada "aaaabbbbccccdd"  ==  True

(duplica xs) es la lista obtenida duplicando los elementos de xs que no lo están. Por ejemplo,

duplica "b"        ==  "bb"
duplica "abba"     ==  "aabbaa"
duplica "Betis"    ==  "BBeettiiss"
duplica [1,1,1]    ==  [1,1,1,1]
duplica [1,1,1,1]  ==  [1,1,1,1]

Comprobar con QuickCheck que, para cualquier lista de enteros xs, se verifica la siguiente propiedad:

esDuplicada (duplica xs)

Ordenación por una fila

José A. Alonso

22-12-2016

Misceláneas

Las matrices se pueden representar por listas de lista. Por ejemplo, la matriz

|1 2 5|
|3 0 7|
|9 1 6|
|6 4 2|

se puede representar por

ej :: [[Int]]
ej = [[1,2,5],
      [3,0,7],
      [9,1,6],
      [6,4,2]]

Definir la función

ordenaPorFila :: Ord a => [[a]] -> Int -> [[a]]

tal que (ordenaPorFila xss k) es la matriz obtenida ordenando xs por los elementos de la fila k. Por ejemplo,

ordenaPorFila ej 1  ==  [[2,1,5],[0,3,7],[1,9,6],[4,6,2]]
ordenaPorFila ej 2  ==  [[2,5,1],[0,7,3],[1,6,9],[4,2,6]]
ordenaPorFila ej 3  ==  [[5,2,1],[7,0,3],[6,1,9],[2,4,6]]

Día de la semana

José A. Alonso

21-12-2016

Misceláneas

Definir la función

dia :: Int -> Int -> Int -> String

tal que (dia d m a) es el día de la semana correspondiente al día d del mes m del año a. Por ejemplo,

dia 21 12 2016  ==  "Miercoles"
dia 14  4 1936  ==  "Martes"

Ordenación por una columna

José A. Alonso

20-12-2016

Misceláneas

Las matrices se pueden representar por listas de lista. Por ejemplo, la matriz

|1 2 5|
|3 0 7|
|9 1 6|
|6 4 2|

se puede representar por

ej :: [[Int]]
ej = [[1,2,5],
      [3,0,7],
      [9,1,6],
      [6,4,2]]

Definir la función

ordenaPor :: Ord a => [[a]] -> Int -> [[a]]

tal que (ordenaPor xss k) es la matriz obtenida ordenando xs por los elementos de la columna k. Por ejemplo,

ordenaPor ej 0  ==  [[1,2,5],[3,0,7],[6,4,2],[9,1,6]]
ordenaPor ej 1  ==  [[3,0,7],[9,1,6],[1,2,5],[6,4,2]]
ordenaPor ej 2  ==  [[6,4,2],[1,2,5],[9,1,6],[3,0,7]]

Selección por posición

José A. Alonso

19-12-2016

Misceláneas

Definir la función

seleccion :: Ord a => [a] -> [Int] -> [a]

tal que (seleccion xs ps) es la lista ordenada de los elementos que ocupan las posiciones indicadas en la lista ps. Por ejemplo,

seleccion [6,2,4,7] [2,0]      ==  [4,6]
seleccion ['a'..'z'] [0,2..10] ==  "acegik"

Números de la suerte

José A. Alonso

16-12-2016

Misceláneas

Un número de la suerte es un número natural que se genera por una criba, similar a la criba de Eratóstenes, como se indica a continuación:

Se comienza con la lista de los números enteros a partir de 1:

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25...

Se eliminan los números de dos en dos

1,  3,  5,  7,  9,   11,   13,   15,   17,   19,   21,   23,   25...

Como el segundo número que ha quedado es 3, se eliminan los números restantes de tres en tres:

1,  3,      7,  9,         13,   15,         19,   21,         25...

Como el tercer número que ha quedado es 7, se eliminan los números restantes de siete en siete:

1,  3,      7,  9,         13,   15,               21,         25...

Este procedimiento se repite indefinidamente y los supervivientes son los números de la suerte:

1,3,7,9,13,15,21,25,31,33,37,43,49,51,63,67,69,73,75,79

Definir la sucesión

numerosDeLaSuerte :: [Int]

cuyos elementos son los números de la suerte. Por ejemplo,

λ> take 20 numerosDeLaSuerte
[1,3,7,9,13,15,21,25,31,33,37,43,49,51,63,67,69,73,75,79]
λ> numerosDeLaSuerte !! 1500
13995

Posiciones de equilibrio

José A. Alonso

15-12-2016

Misceláneas

Se dice que k es una posición de equilibrio de una lista xs si la suma de los elementos de xs en las posiciones menores que k es igual a la suma de los elementos de xs en las posiciones mayores que k. Por ejemplo, en la lista [-7,1,5,2,-4,3,0] el 3 es una posición de equilibrio ya que -7+1+5 = -4+3+0; también lo es el 6 ya que -7+1+5+2+(-4)+3 = 0.

Definir la función,

equilibrios :: (Num a, Eq a) => [a] -> [Int]

tal que (equilibrios xs) es la lista de las posiciones de equilibrio de xs. Por ejemplo,

equilibrios [-7,1,5,2,-4,3,0]  ==  [3,6]
equilibrios [1..10^6]          ==  []

Distancia a Erdős

José A. Alonso

14-12-2016

Misceláneas

Una de las razones por la que el matemático húngaro Paul Erdős es conocido es por la multitud de colaboraciones que realizó durante toda su carrera, un total de 511. Tal es así que se establece la distancia a Erdős como la distancia que has estado de coautoría con Erdős. Por ejemplo, si eres Paul Erdős tu distancia a Erdős es 0, si has escrito un artículo con Erdős tu distancia es 1, si has escrito un artículo con alguien que ha escrito un artículo con Erdős tu distancia es 2, etc. El objetivo de este problema es definir una función que a partir de una lista de pares de coautores y un número natural n calcular la lista de los matemáticos a una distancia n de Erdős.

Para el problema se considerará la siguiente lista de coautores

coautores :: [(String,String)]
coautores =
  [("Paul Erdos","Ernst Straus"),("Paul Erdos","Pascual Jordan"),
   ("Paul Erdos","D. Kleitman"),("Albert Einstein","Ernst Straus"),
   ("John von Newmann","David Hilbert"),("S. Glashow","D. Kleitman"),
   ("John von Newmann","Pascual Jordan"), ("David Pines","D. Bohm"),
   ("Albert Einstein","Otto Stern"),("S. Glashow", "M. Gell-Mann"),
   ("Richar Feynman","M. Gell-Mann"),("M. Gell-Mann","David Pines"),
   ("David Pines","A. Bohr"),("Wolfgang Pauli","Albert Einstein"),
   ("D. Bohm","L. De Broglie"), ("Paul Erdos","J. Conway"),
   ("J. Conway", "P. Doyle"),("Paul Erdos","A. J. Granville"),
   ("A. J. Granville","B. Mazur"),("B. Mazur","Andrew Wiles")]

Definir la función

numeroDeErdos :: [(String, String)] -> Int -> [String]

tal que (numeroDeErdos xs n) es la lista de lista de los matemáticos de la lista de coautores xs que se encuentran a una distancia n de Erdős. Por ejemplo,

λ> numeroDeErdos coautores 0
["Paul Erdos"]
λ> numeroDeErdos coautores 1
["Ernst Straus","Pascual Jordan","D. Kleitman","J. Conway","A. J. Granville"]
λ> numeroDeErdos coautores 2
["Albert Einstein","John von Newmann","S. Glashow","P. Doyle","B. Mazur"]

Agrupación por orden de aparición

José A. Alonso

13-12-2016

Misceláneas

Definir la función

agrupacion :: Eq a => [a] -> [a]

tal que (agrupacion xs) es la lista obtenida agrupando los elementos de xs según su primera aparición. Por ejemplo,

agrupacion [3,1,5,1,7,1,5,3]  ==  [3,3,1,1,1,5,5,7]
agrupacion "babcacb"          ==  "bbbaacc"

Mayores que la mitad

José A. Alonso

12-12-2016

Misceláneas

Definir la función

mayoresMitad :: Ord a => [a] -> [a]

tal que (mayoresMitad xs) es la lista de los elementos de xs que son mayores que la mitad de los elementos de xs, suponiendo que los elementos de xs son distintos. Por ejemplo,

sort (mayoresMitad [1,6,3,4])    ==  [4,6]
sort (mayoresMitad [1,6,3,4,7])  ==  [4,6,7]
sort (mayoresMitad [1,6,3,4,2])  ==  [3,4,6]
length (mayoresMitad3 [1..10^6]) ==  500000

Nota: Se considera que si la lista tiene 2n+1 elementos, su mitad tiene n elementos.

Caracteres en la misma posición que en el alfabeto

José A. Alonso

09-12-2016

Misceláneas

Un carácter c de una cadena cs está bien colocado si la posición de c en cs es la misma que en el abecedario (sin distinguir entre mayúsculas y minúsculas). Por ejemplo, los elementos bien colocados de la cadena "aBaCEria" son 'a', 'B' y 'E'.

Definir la función

nBienColocados :: String -> Int

tal que (nBienColocados cs) es el número de elementos bien colocados de la cadena cs. Por ejemplo,

nBienColocados "aBaCEria"                    ==  3
nBienColocados "xBxxExxxIxxxxNxxxxxTxxxXYZ"  ==  8

Suma de los máximos de los subconjuntos

José A. Alonso

08-12-2016

Misceláneas

Los subconjuntos distinto del vacío del conjunto {3, 2, 5}, junto con sus máximos elementos, son

{3}       su máximo es 3
{2}       su máximo es 2
{5}       su máximo es 5
{3, 2}    su máximo es 3
{3, 5}    su máximo es 5
{2, 5}    su máximo es 5
{3, 2, 5} su máximo es 5

Por tanto, la suma de los máximos elementos de los subconjuntos de {3, 2, 5} es 3 + 2 + 5 + 3 + 5 + 5 + 5 = 28.

Definir la función

sumaMaximos :: [Integer] -> Integer

tal que (sumaMaximos xs) es la suma de los máximos elementos de los subconjuntos de xs. Por ejemplo,

sumaMaximos [3,2,5]    ==  28
sumaMaximos [4,1,6,3]  ==  71
sumaMaximos [1..100]   ==  125497409422594710748173617332225
length (show (sumaMaximos [1..10^5]))  ==  30108
sumaMaximos [1..10^5] `mod` (10^7)     ==  4490625

Elementos que respetan la ordenación

José A. Alonso

07-12-2016

Misceláneas

Se dice que un elemento x de una lista xs respeta la ordenación si x es mayor o igual que todos lo que tiene delante en xs y es menor o igual que todos lo que tiene detrás en xs. Por ejemplo, en la lista lista [3,2,1,4,6,5,7,9,8] el número 4 respeta la ordenación pero el número 5 no la respeta (porque es mayor que el 6 que está delante).

Definir la función

respetuosos :: Ord a => [a] -> [a]

tal que (respetuosos xs) es la lista de los elementos de xs que respetan la ordenación. Por ejemplo,

respetuosos [3,2,1,4,6,4,7,9,8]  ==  [4,7]
respetuosos [2,1,3,4,6,4,7,8,9]  ==  [3,4,7,8,9]
respetuosos "abaco"              ==  "aco"
respetuosos "amor"               ==  "amor"
respetuosos "romanos"            ==  "s"
respetuosos [1..9]               ==  [1,2,3,4,5,6,7,8,9]
respetuosos [9,8..1]             ==  []

Comprobar con QuickCheck que para cualquier lista de enteros xs se verifican las siguientes propiedades:

todos los elementos de (sort xs) respetan la ordenación y
en la lista (nub (reverse (sort xs))) hay como máximo un elemento que respeta la ordenación.

Sin ceros finales

José A. Alonso

06-12-2016

Misceláneas

Definir la función

sinCerosFinales :: Int -> Int

tal que (sinCerosFinales n) es el número obtenido eliminando los ceros finales de n. Por ejemplo,

sinCerosFinales 104050     == 10405
sinCerosFinales 960000     == 96
sinCerosFinales 100050     == 10005
sinCerosFinales (-10050)   == -1005
sinCerosFinales 12         == 12
sinCerosFinales 0          == 0

Comprobar con QuickCheck que, para cualquier número entero n,

sinCerosFinales (sinCerosFinales n) == sinCerosFinales n

Listas engarzadas

José A. Alonso

03-12-2016

Misceláneas

Una lista de listas es engarzada si el último elemento de cada lista coincide con el primero de la siguiente.

Definir la función

engarzada :: Eq a => [[a]] -> Bool

tal que (engarzada xss) se verifica si xss es una lista engarzada. Por ejemplo,

engarzada [[1,2,3], [3,5], [5,9,0]] == True
engarzada [[1,4,5], [5,0], [1,0]]   == False
engarzada [[1,4,5], [], [1,0]]      == False
engarzada [[2]]                     == True

Listas alternadas

José A. Alonso

02-12-2016

Misceláneas

Una lista de números enteros se llama alternada si sus elementos son alternativamente par/impar o impar/par.

Definir la función

alternada :: [Int] -> Bool

tal que (alternada xs) se verifica si xs es una lista alternada. Por ejemplo,

alternada [1,2,3]     == True
alternada [1,4,6,5]   == False
alternada [1,4,3,5]   == False
alternada [8,1,2,3,4] == True
alternada [8,1,2,3]   == True
alternada [8]         == True
alternada [7]         == True

Sumas de posiciones pares e impares

José A. Alonso

01-12-2016

Misceláneas

Definir la función

sumasParesImpares :: [Integer] -> (Integer,Integer)

tal que (sumasParesImpares) xs es el par formado por la suma de los elementos de xs en posiciones pares y por la suma de los elementos de xs en posiciones impares. Por ejemplo,

sumasParesImpares []         ==  (0,0)
sumasParesImpares [3]        ==  (3,0)
sumasParesImpares [3,2]      ==  (3,2)
sumasParesImpares [3,2,1]    ==  (4,2)
sumasParesImpares [3,2,1,5]  ==  (4,7)
sumasParesImpares [1..10^7]  ==  (25000000000000,25000005000000)

Problema de las particiones óptimas

José A. Alonso

30-11-2016

Misceláneas

El problema de la particiones óptimas consiste en dada una lista xs dividirla en dos sublistas ys y zs tales que el valor absoluto de la diferencia de la suma de los elementos de xs y la suma de los elemento de zs sea lo menor posible.Cada una de estas divisiones (ys,zs) es una partición óptima de xs. Por ejemplo, la partición óptima de [2,3,5] es ([2,3],[5]) ya que |(2+3) - 5| = 0. Una lista puede terner distintas particiones óptimas. Por ejemplo, [1,1,2,3] tiene dos particiones óptimas ([1,2],[1,3]) y ([1,1,2],[3]) ambas con diferencia 1 (es decir, 1 = |(1+2)-(1+3)| = |(1+1+2)-3|.

Definir la función

particionesOptimas :: [Int] -> ([Int],[Int])

tal que (particionesOptimas xs) es la lista de las particiones óptimas de xs. Por ejemplo,

particionesOptimas [2,3,5]    ==  [([2,3],[5])]
particionesOptimas [1,1,2,3]  ==  [([1,2],[1,3]),([1,1,2],[3])]
particionesOptimas [5,0,5]    ==  [([0,5],[5])]
particionesOptimas [5,5]      ==  [([5],[5])]
particionesOptimas [5]        ==  [([],[5])]

Huecos de Euclides

José A. Alonso

29-11-2016

Misceláneas

El teorema de Euclides afirma que existen infinitos números primos. En palabras de Euclides,

"Hay más números primos que cualquier cantidad propuesta de números primos." (Proposición 20 del Libro IX de "Los Elementos").

Su demostración se basa en que si p₁,...,pₙ son los primeros n números primos, entonces entre 1+pₙ y 1+p₁·p₂·...·pₙ hay algún número primo. La cantidad de dichos números primos se llama el n-ésimo hueco de Euclides. Por ejemplo, para n = 3 se tiene que p₁ = 2, p₂ = 3 y p₃ = 5 entre 1+p₃ = 6 y 1+p₁·p₂·p₃ = 31 hay 8 números primos (7, 11, 13, 17, 19, 23, 29 y 31), por lo que el valor del tercer hueco de Euclides es 8.

Definir la función

hueco :: Int -> Integer

tal que (hueco n) es el n-ésimo hueco de Eulides. Por ejemplo,

hueco 3                   ==  8
[hueco n | n <- [1..8]]   ==  [1,2,8,43,339,3242,42324,646021]

Representación binaria de los números de Carol

José A. Alonso

28-11-2016

Misceláneas

Un número de Carol es un número entero de la forma \(4^n-2^{n+1}-1\) o, equivalentemente, \((2^n-1)^2-2\). Los primeros números de Carol son -1, 7, 47, 223, 959, 3967, 16127, 65023, 261119, 1046527.

Definir las funciones

carol        :: Integer -> Integer
carolBinario :: Integer -> Integer

tales que

(carol n) es el n-ésimo número de Carol. Por ejemplo,

carol  3  ==  47
carol  4  ==  223
carol 25  ==  1125899839733759

(carolBinario n) es la representación binaria del n-ésimo número de Carol. Por ejemplo,

carolBinario 3  ==  101111
carolBinario 4  ==  11011111
carolBinario 5  ==  1110111111

Comprobar con QuickCheck que, para n > 2, la representación binaria del n-ésimo número de Carol es el número formado por n-2 veces el dígito 1, seguido por un 0 y a continuación n+1 veces el dígito 1.

Mínimo número de operaciones para transformar un número en otro

José A. Alonso

25-11-2016

Misceláneas

Se considera el siguiente par de operaciones sobre los números:

multiplicar por dos
restar uno.

Dados dos números x e y se desea calcular el menor número de operaciones para transformar x en y. Por ejemplo, el menor número de operaciones para transformar el 4 en 7 es 2:

4 ------> 8 ------> 7
   (x2)      (-1)

y el menor número de operaciones para transformar 2 en 5 es 4

2 ------> 4 ------> 3 ------> 6 ------> 5
   (x2)      (-1)      (x2)      (-1)

Definir las siguientes funciones

arbolOp :: Int -> Int -> Arbol
minNOp  :: Int -> Int -> Int

tales que

(arbolOp x n) es el árbol de profundidad n obtenido aplicándole a x las dos operaciones. Por ejemplo,

    λ> arbolOp 4 1
    N 4 (H 8) (H 3)
    λ> arbolOp 4 2
    N 4 (N 8 (H 16) (H 7))
        (N 3 (H 6) (H 2))
    λ> arbolOp 2 3
    N 2 (N 4
           (N 8 (H 16) (H 7))
           (N 3 (H 6) (H 2)))
        (N 1
           (N 2 (H 4) (H 1))
           (H 0))
    λ> arbolOp 2 4
    N 2 (N 4 (N 8
                (N 16 (H 32) (H 15))
                (N 7 (H 14) (H 6)))
             (N 3
                (N 6 (H 12) (H 5))
                (N 2 (H 4) (H 1))))
        (N 1 (N 2
                (N 4 (H 8) (H 3))
                (N 1 (H 2) (H 0)))
             (H 0))

(minNOp x y) es el menor número de operaciones necesarias para transformar x en y. Por ejemplo,

minNOp 4 7  ==  2
minNOp 2 5  ==  4

Menor potencia de 2 comenzando un número dado

José A. Alonso

24-11-2016

Misceláneas

Definir las siguientes funciones

potenciasDe2  :: Integer -> [Integer]
menorPotenciaDe2 :: Integer -> Integer

tales que

(potenciasDe2 a) es la lista de las potencias de 2 que comienzan por a. Por ejemplo,

λ> take 5 (potenciasDe2 3)
[32,32768,33554432,34359738368,35184372088832]
λ> take 2 (potenciasDe2 102)
[1024,102844034832575377634685573909834406561420991602098741459288064]

(menorPotenciaDe2 a) es la menor potencia de 2 que comienza con el número a. Por ejemplo,

λ> menorPotenciaDe2 10
1024
λ> menorPotenciaDe2 25
256
λ> menorPotenciaDe2 62
6277101735386680763835789423207666416102355444464034512896
λ> menorPotenciaDe2 425
42535295865117307932921825928971026432
λ> menorPotenciaDe2 967140655691
9671406556917033397649408
λ> [menorPotenciaDe2 a | a <- [1..10]]
[1,2,32,4,512,64,70368744177664,8,9007199254740992,1024]

Comprobar con QuickCheck que, para todo entero positivo a, existe una potencia de 2 que empieza por a.

Máxima ramificación

José A. Alonso

23-11-2016

Misceláneas

Los árboles se pueden representar mediante el siguiente tipo de datos

data Arbol a = N a [Arbol a]
               deriving Show

Por ejemplo, los árboles

  1         1             1
 / \       / \           / \
2   3     2   3         2   3
    |        /|\       /|\  |
    4       4 5 6     4 5 6 7

se representan por

ej1, ej2, ej3 :: Arbol Int
ej1 = N 1 [N 2 [],N 3 [N 4 []]]
ej2 = N 1 [N 2 [], N 3 [N 4 [], N 5 [], N 6 []]
ej3 = N 1 [N 2 [N 4 [], N 5 [], N 6 []], N 3 [N 7 []]]

En el primer ejemplo la máxima ramificación es 2 (en el nodo 1 que tiene 2 hijos), la del segundo es 3 (en el nodo 3 que tiene 3 hijos) y la del tercero es 3 (en el nodo 3 que tiene 3 hijos).

Definir la función

maximaRamificacion :: Arbol a -> Int

tal que (maximaRamificacion a) es la máxima ramificación del árbol a. Por ejemplo,

maximaRamificacion ej1  ==  2
maximaRamificacion ej2  ==  3
maximaRamificacion ej3  ==  3

Números consecutivos compuestos

José A. Alonso

22-11-2016

Misceláneas

Una serie compuesta de longitud n es una lista de n números consecutivos que son todos compuestos. Por ejemplo, [8,9,10] y [24,25,26] son dos series compuestas de longitud 3.

Cada serie compuesta se puede representar por el par formado por su primer y último elemento. Por ejemplo, las dos series anteriores se pueden representar pos (8,10) y (24,26) respectivamente.

Definir la función

menorSerieCompuesta :: Integer -> (Integer,Integer)

tal que (menorSerieCompuesta n) es la menor serie compuesta (es decir, la que tiene menores elementos) de longitud 3. Por ejemplo,

menorSerieCompuesta 3    ==  (8,10)
menorSerieCompuesta 4    ==  (24,27)
menorSerieCompuesta 5    ==  (24,28)
menorSerieCompuesta 150  ==  (4652354,4652503)

Comprobar con QuickCheck que para n > 1, el primer elemento de (menorSerieCompuesta n) es igual al primero de (menorSerieCompuesta (n-1)) o al primero de (menorSerieCompuesta (n+1)).

Conmutaciones ondulantes

José A. Alonso

21-11-2016

Misceláneas

Una lista binaria es ondulante si sus elementos son alternativamente 0 y 1. Por ejemplo, las listas [0,1,0,1,0] y [1,0,1,0] son ondulantes.

Definir la función

minConmutacionesOndulante :: [Int] -> Int

tal que (minConmutacionesOndulante xs) es el mínimo número de conmutaciones (es decir, cambios de 0 a 1 o de 1 a 0) necesarias para transformar xs en una lista ondulante. Por ejemplo,

minConmutacionesOndulante [1,1,1]                ==  1
minConmutacionesOndulante [0,0,0,1,0,1,0,1,1,1]  ==  2

En el primer ejemplo basta conmutar el elemento en la posición 1 para obtener [1,0,1] y el segundo ejemplo los elementos en las posiciones 1 y 8 para obtener [0,1,0,1,0,1,0,1,0,1].

Números de Dudeney

José A. Alonso

18-11-2016

Misceláneas

La semana pasada, Pepe Muñoz Santonja publicó en su blog Algo más que números el artículo Números de Dudeney en la base OEIS.

Un número de Dudeney es un número entero n tal que el cubo de la suma de sus dígitos es igual a n. Por ejemplo, 512 es un número de Dudeney ya que (5+1+2)^3 = 8^3 = 512.

Se puede generalizar variando el exponente: Un número de Dudeney de orden k es un número entero n tal que la potencia k-ésima de la suma de sus dígitos es igual a n. Por ejemplo, 2401 es un número de Dudeney de orden 4 ya que (2+4+0+1)^4 = 7^4 = 2401.

Definir la función

numerosDudeney :: Integer -> [Integer]

tal que (numerosDudeney k) es la lista de los números de Dudeney oe orden k. Por ejemplo,

take 6 (numerosDudeney 3)  == [1,512,4913,5832,17576,19683]
take 6 (numerosDudeney 4)  == [1,2401,234256,390625,614656,1679616]
take 2 (numerosDudeney 20) == [1,1215766545905692880100000000000000000000]

Comprobar con QuickCheck que 19683 es el mayor número de Dudeney de orden 3.

Números poderosos

José A. Alonso

17-11-2016

Misceláneas

Un número es poderoso si es igual a la suma de sus dígitos elevados a sus respectivas posiciones. Por ejemplo, los números 89, 135 y 1306 son poderosos ya que

  89 = 8^1 + 9^2
 135 = 1^1 + 3^2 + 5^3.
1306 = 1^1 + 3^2 + 0^3 + 6^4

Definir la función

esPoderoso :: Integer -> Bool

tal que (esPoderoso n) se verifica si n es poderoso. Por ejemplo,

λ> esPoderoso 135
True
λ> esPoderoso 80
False
λ> esPoderoso 89
True
λ> esPoderoso 12157692622039623539
True
λ> [n | n <- [10..30000], esPoderoso n]
[89,135,175,518,598,1306,1676,2427]

Comprobar con QuickCheck que 12157692622039623539 es el mayor número poderoso.

Máximo producto en la partición de un número

José A. Alonso

16-11-2016

Misceláneas

El artículo de esta semana de Antonio Roldán en su blog Números y hoja de cálculo es Máximo producto en la partición de un número (1).

Una partición de un entero positivo n es una forma de descomponer n como suma de enteros positivos. Dos sumas se considerarán iguales si solo difieren en el orden de los sumandos. Por ejemplo, las 11 particiones de 6 (con sus correspondientes productos) son

6 = 6                      |  6                     = 6
6 = 5 + 1                  |  5 x 1                 = 5
6 = 4 + 2                  |  4 x 2                 = 8
6 = 4 + 1 + 1              |  4 x 1 x 1             = 4
6 = 3 + 3                  |  3 x 3                 = 9
6 = 3 + 2 + 1              |  3 x 2 x 1             = 6
6 = 3 + 1 + 1 + 1          |  3 x 1 x 1 x 1         = 3
6 = 2 + 2 + 2              |  2 x 2 x 2             = 8
6 = 2 + 2 + 1 + 1          |  2 x 2 x 1 x 1         = 4
6 = 2 + 1 + 1 + 1 + 1      |  2 x 1 x 1 x 1 x 1     = 2
6 = 1 + 1 + 1 + 1 + 1 + 1  |  1 x 1 x 1 x 1 x 1 x 1 = 1

Se observa que el máximo producto de las particiones de 6 es 9.

Definir la función

maximoProductoParticiones :: Int -> Int

tal que (maximoProductoParticiones n) es el máximo de los productos de las particiones de n. Por ejemplo,

maximoProductoParticiones 4     ==  4
maximoProductoParticiones 5     ==  6
maximoProductoParticiones 6     ==  9
maximoProductoParticiones 7     ==  12
maximoProductoParticiones 8     ==  18
maximoProductoParticiones 9     ==  27
maximoProductoParticiones 50    ==  86093442
maximoProductoParticiones 100   ==  7412080755407364
maximoProductoParticiones 200   ==  61806308765265224723841283607058
length (show (maximoProductoParticiones (10^7)))  ==  1590405

Comprobar con QuickChek que los únicos posibles factores de (maximoProductoParticiones n) son 2 y 3.

Cuadrados ondulantes

José A. Alonso

15-11-2016

Misceláneas

Un número se dice ondulante si sus cifras alternan entre dos valores. Por ejemplo, 272 es ondulante, así como 2727. El primer cuadrado ondulante no trivial (todos los cuadrados de dos cifras son ondulantes) es 121 = 11^2.

Definir la función

cuadradosOndulantes :: Integer -> [Integer]

tal que (cuadradosOndulantes n) es la lista de los cuadrados ondulantes menores que n^2. Por ejemplo,

λ> cuadradosOndulantes 50000
[0,1,4,9,16,25,36,49,64,81,121,484,676,69696]

Persistencia multiplicativa de un número

José A. Alonso

14-11-2016

Misceláneas

La persistencia multiplicativa de un número es la cantidad de pasos requeridos para reducirlo a una cifra multiplicando sus dígitos. Por ejemplo, la persistencia de 39 es 3 porque 3×9 = 27, 2×7 = 14 y 1×4 = 4.

Definir las funciones

persistencia     :: Integer -> Integer
menorPersistente :: Integer -> Integer

tales que

(persistencia x) es la persistencia de x. Por ejemplo,

persistencia 39                             ==   3
persistencia 2677889                        ==   8
persistencia 26888999                       ==   9
persistencia 3778888999                     ==  10
persistencia 277777788888899                ==  11
persistencia 77777733332222222222222222222  ==  11

(menorPersistente n) es el menor número con persistencia n. Por ejemplo,

menorPersistente 0  ==  1
menorPersistente 1  ==  10
menorPersistente 2  ==  25
menorPersistente 3  ==  39
menorPersistente 4  ==  77
menorPersistente 5  ==  679
menorPersistente 6  ==  6788
menorPersistente 7  ==  68889

Comprobar con QuickCheck si todos los números menores que 10^233 tienen una persistencia multiplicativa menor o igual que 11.

Números perfectos y cojonudos

José A. Alonso

11-11-2016

Misceláneas

Un número perfecto es un número entero positivo que es igual a la suma de sus divisores propios. Por ejemplo, el 28 es perfecto porque sus divisores propios son 1, 2, 4, 7 y 14 y 1+2+4+7+14 = 28.

Un entero positivo x es un número cojonudo si existe un n tal que n > 0, x = 2^n·(2^(n+1)-1) y 2^(n+1)-1 es primo. Por ejemplo, el 28 es cojonudo ya que para n = 2 se verifica que 2 > 0, 28 = 2^2·(2^3-1) y 2^3-1 = 7 es primo.

Definir la funciones

esPerfecto                      :: Integer -> Bool
esCojonudo                      :: Integer -> Bool
equivalencia_CojonudosPerfectos :: Integer -> Bool

tales que

(esPerfecto x) se verifica si x es perfecto. Por ejemplo,

esPerfecto 28  ==  True
esPerfecto 30  ==  False

(esCojonudo x) se verifica si x es cojonudo. Por ejemplo,

esCojonudo 28                   ==  True
esCojonudo 30                   ==  False
esCojonudo 2305843008139952128  ==  True

(equivalenciaCojonudosPerfectos n) se verifica si para todos los números x menores o iguales que n se tiene que x es perfecto si, y sólo si, x es cojonudo. Por ejemplo,

equivalenciaCojonudosPerfectos 3000  ==  True

Subconjuntos acotados

José A. Alonso

10-11-2016

Misceláneas

Definir la función

subconjuntosAcotados :: [a] -> Int -> [[a]]

tal que (subconjuntosAcotados xs k) es la lista de los subconjuntos de xs con k elementos como máximo. Por ejemplo,

λ> subconjuntosAcotados "abcd" 1
["a","b","c","d",""]
λ> subconjuntosAcotados "abcd" 2
["ab","ac","ad","a","bc","bd","b","cd","c","d",""]
λ> subconjuntosAcotados "abcd" 3
["abc","abd","ab","acd","ac","ad","a",
 "bcd","bc","bd","b","cd","c","d",""]
λ> length (subconjuntosAcotados [1..1000] 2)
500501
λ> length (subconjuntosAcotados2 [1..2000] 2)
2001001

Variación de la conjetura de Goldbach

José A. Alonso

09-11-2016

Misceláneas

La conjetura de Goldbach afirma que

Todo número entero mayor que 5 se puede escribir como suma de tres números primos.

En este ejercicio consideraremos la variación consistente en exigir que los tres sumandos sean distintos.

Definir las funciones

sumas3PrimosDistintos      :: Int -> [(Int,Int,Int)]
conKsumas3PrimosDistintos  :: Int -> Int -> [Int]
noSonSumas3PrimosDistintos :: Int -> [Int]

tales que

(sumas3PrimosDistintos n) es la lista de las descomposiciones decrecientes de n como tres primos distintos. Por ejemplo,

sumas3PrimosDistintos 26  ==  [(13,11,2),(17,7,2),(19,5,2)]
sumas3PrimosDistintos 18  ==  [(11,5,2),(13,3,2)]
sumas3PrimosDistintos 10  ==  [(5,3,2)]
sumas3PrimosDistintos 11  ==  []

(conKsumas3PrimosDistintos k n) es la lista de los números menores o iguales que n que se pueden escribir en k forma distintas como suma de tres primos distintos. Por ejemplo,

conKsumas3PrimosDistintos 3 99  ==  [26,27,29,32,36,42,46,48,54,58,60]
conKsumas3PrimosDistintos 2 99  ==  [18,20,21,22,23,24,25,28,30,34,64,70]
conKsumas3PrimosDistintos 1 99  ==  [10,12,14,15,16,19,40]
conKsumas3PrimosDistintos 0 99  ==  [11,13,17]

(noSonSumas3PrimosDistintos n) es la lista de los números menores o iguales que n que no se pueden escribir como suma de tres primos distintos. Por ejemplo,

noSonSumas3PrimosDistintos 99   ==  [11,13,17]
noSonSumas3PrimosDistintos 500  ==  [11,13,17]

Conjetura de Rassias

José A. Alonso

08-11-2016

Misceláneas

El artículo de esta semana del blog Números y hoja de cálculo está dedicado a la Conjetura de Rassias. Dicha conjetura afirma que

Para cada número primo p > 2 existen dos primos a y b, con a < b, tales que (p-1)a = b+1

Dado un primo p > 2, los pares de Rassia de p son los pares de primos (a,b), con a < b, tales que (p-1)a = b+1. Por ejemplo, (2,7) y (3,11) son pares de Rassia de 5 ya que

2 y 7 son primos, 2 < 7 y (5-1)·2 = 7+1
3 y 11 son primos, 3 < 11 y (5-1)·3 = 11+1

Definir las siguientes funciones

paresRassias     :: Integer -> [(Integer,Integer)]
conjeturaRassias :: Integer -> Bool

tales que

(paresRassias p) es la lista de los pares de Rassias del primo p (que se supone que es mayor que 2). Por ejemplo,

take 3 (paresRassias 5)    == [(2,7),(3,11),(5,19)]
take 3 (paresRassias 1229) == [(71,87187),(113,138763),(191,234547)]

(conjeturaRassia x) se verifica si para todos los primos menores que x (y mayores que 2) se cumple la conjetura de Rassia. Por ejemplo,

conjeturaRassias (10^5)  ==  True

Primo anterior

José A. Alonso

07-11-2016

Misceláneas

Definir la función

primoAnterior :: Integer -> Integer

tal que (primoAnterior n) es el mayor primo menor que n (donde n > 2). Por ejemplo,

primoAnterior 10     ==  7
primoAnterior 17     ==  13
primoAnterior 30     ==  29
primoAnterior 2016   ==  2011
primoAnterior 15726  ==  15683

Calcular el menor número cuya distancia a su primo anterior es mayor que 40.

Primos de Kamenetsky

José A. Alonso

04-11-2016

Misceláneas

Un número primo se dice que es un primo de Kamenetsky si al anteponerlo cualquier dígito se obtiene un número compuesto. Por ejemplo, el 5 es un primo de Kamenetsky ya que 15, 25, 35, 45, 55, 65, 75, 85 y 95 son compuestos. También lo es 149 ya que 1149, 2149, 3149, 4149, 5149, 6149, 7149, 8149 y 9149 son compuestos.

Definir la sucesión

primosKamenetsky :: [Integer]

tal que sus elementos son los números primos de Kamenetsky. Por ejemplo,

take 5 primosKamenetsky  ==  [2,5,149,401,509]

Números de Harshad hereditarios

José A. Alonso

03-11-2016

Misceláneas

Un número de Harshad es un entero divisible entre la suma de sus dígitos. Por ejemplo, 201 es un número de Harshad porque es divisible por 3 (la suma de sus dígitos). Cuando se elimina el último dígito de 201 se obtiene 20 que también es un número de Harshad. Cuando se elimina el último dígito de 20 se obtiene 2 que también es un número de Harshad. Los números como el 201 que son de Harshad y que los números obtenidos eliminando sus últimos dígitos siguen siendo de Harshad se llaman números de Harshad hereditarios por la derecha. Definir la función

numeroHHD :: Int -> Bool

tal que (numeroHHD n) se verifica si n es un número de Harshad hereditario por la derecha. Por ejemplo,

numeroHHD 201  ==  True
numeroHHD 140  ==  False
numeroHHD 1104 ==  False

Calcular el mayor número de Harshad hereditario por la derecha con tres dígitos.

Triángulos geométricos

José A. Alonso

01-11-2016

Misceláneas

Un triángulo geométrico es un triángulo de lados enteros, representados por la terna (a,b,c) tal que a ≤ b ≤ c y están en progresión geométrica, es decir, b^2 = a*c. Por ejemplo, un triángulo de lados a = 144, b = 156 y c = 169.

Definir la función

numeroTG :: Integer -> Int

tal que (numeroTG n) es el número de triángulos geométricos de perímetro menor o igual que n. Por ejemplo

numeroTG 10  == 3
numeroTG 100 == 42
numeroTG 200 == 91

Nota: Los triángulos geométricos de perímetro menor o igual que 20 son

[(1,1,1),(2,2,2),(3,3,3),(4,4,4),(5,5,5),(6,6,6),(4,6,9)]

Se observa que (1,2,4) aunque cumple que 1+2+4 <= 10 y 2^2 = 1*4 no pertenece a la lista ya que 1+2 > 4 y, por tanto, no hay ningún triángulo cuyos lados midan 1, 2 y 4.

Sucesión infinita de todas las palabras

José A. Alonso

31-05-2016

Misceláneas

Cadenas de primos complementarios

José A. Alonso

30-05-2016

Misceláneas

El complemento de un número positivo x se calcula por el siguiente procedimiento:

si x es mayor que 9, se toma cada dígito por su valor posicional y se resta del mayor los otro dígitos. Por ejemplo, el complemento de 1448 es 1000 - 400 - 40 - 8 = 552. Para
si x es menor que 10, su complemento es x.

Definir las funciones

cadena    :: Integer -> [Integer]
conCadena :: Int -> [Integer]

tales que

(cadena x) es la cadena de primos a partir de x tal que cada uno es el complemento del anterior. Por ejemplo,

cadena 8         == []
cadena 7         == [7]
cadena 13        == [13,7]
cadena 643       == [643,557,443]
cadena 18127     == [18127,1873,127,73,67,53,47]
cadena 18181213  == [18181213,1818787,181213,18787,1213,787,613,587]

(conCadena n) es la lista de números cuyas cadenas tienen n elementos. Por ejemplo,

take 6 (conCadena 3)                == [23,31,61,67,103,307]
[head (conCadena n) | n <- [4..8]]  == [37,43,157,18127,181873]

Construcción del árbol a partir de los recorridos preorden e inorden

José A. Alonso

27-05-2016

Misceláneas

Los árboles binarios con valores en las hojas y en los nodos se pueden representar con el siguiente tipo

data Arbol a = H a
             | N a (Arbol a) (Arbol a)
             deriving (Show, Eq)

Por ejemplo, el árbol

se representa por

N 9 (N 3 (H 2) (H 4)) (H 7)

Definir las siguientes funciones

preorden :: Arbol a -> [a]
inorden  :: Arbol a -> [a]
arboles  :: Eq a => [a] -> [a] -> [Arbol a]

tales que

(preorden x) es la lista correspondiente al recorrido preorden del árbol x; es decir, primero visita la raíz del árbol, a continuación recorre el subárbol izquierdo y, finalmente, recorre el subárbol derecho. Por ejemplo,

preorden (N 9 (N 3 (H 2) (H 4)) (H 7))  ==  [9,3,2,4,7]

(inorden x) es la lista correspondiente al recorrido inorden del árbol x; es decir, primero recorre el subárbol izquierdo, a continuación visita la raíz del árbol y, finalmente, recorre el subárbol derecho. Por ejemplo,

inorden (N 9 (N 3 (H 2) (H 4)) (H 7))  ==  [2,3,4,9,7]

(arboles xs ys) es la lista de los árboles con recorrido preorden xs y recorrido inorden de ys. Por ejemplo,

λ> arboles [9,3,2,4,7] [2,3,4,9,7]
[N 9 (N 3 (H 2) (H 4)) (H 7)]
λ> arboles [9,3,2,4,7] [2,4,3,9,7]
[]
λ> arboles [1,1,1,2,3] [1,1,2,1,3]
[N 1 (H 1) (N 1 (H 2) (H 3)),
N 1 (N 1 (H 1) (H 2)) (H 3)]
λ> let x = N 1 (N 1 (H 1) (H 3)) (N 1 (N 1 (H 1) (H 2)) (H 3))
λ> arboles (preorden x) (inorden x)
[N 1 (H 1) (N 1 (H 3) (N 1 (H 1) (N 1 (H 2) (H 3)))),
N 1 (H 1) (N 1 (H 3) (N 1 (N 1 (H 1) (H 2)) (H 3))),
N 1 (N 1 (H 1) (H 3)) (N 1 (H 1) (N 1 (H 2) (H 3))),
N 1 (N 1 (H 1) (H 3)) (N 1 (N 1 (H 1) (H 2)) (H 3))]

Comprobar con QuickCheck, que para todo árbol x se verifican las siguientes propiedades

prop_arboles1 :: Arbol Int -> Bool
prop_arboles1 x =
    x `elem` arboles (preorden x) (inorden x)

prop_arboles2 :: Arbol Int -> Bool
prop_arboles2 x =
    and [preorden a == xs && inorden a == ys | a <- as]
    where xs = preorden x
          ys = inorden x
          as = arboles xs ys

Nota: Para la comprobación, se usa el siguiente generador

import Control.Monad

instance Arbitrary a => Arbitrary (Arbol a) where
  arbitrary = sized arbol
    where
      arbol 0       = liftM H arbitrary
      arbol n | n>0 = oneof [liftM H arbitrary,
                             liftM3 N arbitrary subarbol subarbol]
                      where subarbol = arbol (div n 2)

Caminos en una retícula

José A. Alonso

26-05-2016

Misceláneas

El problema de los caminos en una retícula consiste en, dada una retícula rectangular con m filas y n columnas, determinar todos los caminos para ir desde el vértice inferior izquierdo hasta el vértice superior derecho donde los movimientos permitidos son mover hacia el siguiente vértice a la derecha o arriba.

Por ejemplo, en la siguiente retícula un posible camino es el indicado en rojo.

Caminos en una retícula

Para representar los caminos se definen los siguientes tipos de datos:

data Direccion = D | A deriving (Show, Eq)
type Camino = [Direccion]

Por tanto, el camino de la figura anterior se representa por la lista [D,D,A,D,A].

Definir las funciones

caminos  :: Int -> Int -> [Camino]
nCaminos :: Int -> Int -> Integer

tales que

(caminos m n) es la lista de los caminos en una retícula rectangular con m filas y n columnas. Por ejemplo,

λ> caminos 2 2
[[A,A,D,D],[A,D,A,D],[A,D,D,A],[D,A,A,D],[D,A,D,A],[D,D,A,A]]
λ> caminos 1 3
[[A,A,A,D],[A,A,D,A],[A,D,A,A],[D,A,A,A]]
λ> caminos 2 3
[[A,A,A,D,D],[A,A,D,A,D],[A,A,D,D,A],[A,D,A,A,D],[A,D,A,D,A],[A,D,D,A,A],
[D,A,A,A,D],[D,A,A,D,A],[D,A,D,A,A],[D,D,A,A,A]]

(nCaminos m n) es el número de los caminos en una retícula rectangular con m filas y n columnas. Por ejemplo,

nCaminos 2 2  ==  6
nCaminos 1 3  ==  4
nCaminos 2 3  ==  10
length (show (nCaminos 20000 30000))  ==  14612
length (show (nCaminos 30000 20000))  ==  14612

Centro de gravedad de una lista

José A. Alonso

25-05-2016

Misceláneas

Se dice que una lista de números xs es equilibrada si existe una posición k tal que la suma de los elementos de xs en las posiciones menores que k es igual a la de los elementos de xs en las posiciones mayores que k. La posición k se llama el centro de gravedad de xs. Por ejemplo, la lista [1,3,4,5,-2,1] es equilibrada, y su centro de gravedad es 2, ya que la suma de [1,3] es igual a la de [5,-2,1]. En cambio, la lista [1,6,4,5,-2,1] no tiene centro de gravedad.

Definir la función

centro :: (Num a, Eq a) => [a] -> Maybe Int

tal que (centro xs) es justo el centro e gravedad de xs, si la lista xs es equilibrada y Nothing en caso contrario. Por ejemplo,

centro [1,3,4,5,-2,1]           ==  Just 2
centro [1,6,4,5,-2,1]           ==  Nothing
centro [1,2,3,4,3,2,1]          ==  Just 3
centro [1,100,50,-51,1,1]       ==  Just 1
centro [1,2,3,4,5,6]            ==  Nothing
centro [20,10,30,10,10,15,35]   ==  Just 3
centro [20,10,-80,10,10,15,35]  ==  Just 0
centro [10,-80,10,10,15,35,20]  ==  Just 6
centro [0,0,0,0,0]              ==  Just 0
centro [-1,-2,-3,-4,-3,-2,-1]   ==  Just 3

El problema de las N torres

José A. Alonso

24-05-2016

Misceláneas

El problema de las N torres consiste en colocar N torres en un tablero con N filas y N columnas de forma que no haya dos torres en la misma fila ni en la misma columna.

Cada solución del problema de puede representar mediante una matriz con ceros y unos donde los unos representan las posiciones ocupadas por las torres y los ceros las posiciones libres. Por ejemplo,

( 0 1 0 )
( 1 0 0 )
( 0 0 1 )

representa una solución del problema de las 3 torres.

Definir las funciones

torres  :: Int -> [Matrix Int]
nTorres :: Int -> Integer

tales que + (torres n) es la lista de las soluciones del problema de las n torres. Por ejemplo,

λ> torres 3
[( 1 0 0 )
 ( 0 1 0 )
 ( 0 0 1 )
,( 1 0 0 )
 ( 0 0 1 )
 ( 0 1 0 )
,( 0 1 0 )
 ( 1 0 0 )
 ( 0 0 1 )
,( 0 1 0 )
 ( 0 0 1 )
 ( 1 0 0 )
,( 0 0 1 )
 ( 1 0 0 )
 ( 0 1 0 )
,( 0 0 1 )
 ( 0 1 0 )
 ( 1 0 0 )
]

(nTorres n) es el número de soluciones del problema de las n torres. Por ejemplo,

λ> nTorres 3
6
λ> length (show (nTorres (10^4)))
35660

La sucesión del reloj astronómico de Praga

José A. Alonso

23-05-2016

Misceláneas

La cadena infinita "1234321234321234321...", formada por la repetición de los dígitos 123432, tiene una propiedad (en la que se basa el funcionamiento del reloj astronómico de Praga: la cadena se puede partir en una sucesión de números, de forma que la suma de los dígitos de dichos números es la serie de los números naturales, como se observa a continuación:

1, 2, 3, 4, 32, 123, 43, 2123, 432, 1234, 32123, ...
1, 2, 3, 4,  5,   6,  7,    8,   9,   10,    11, ...

Definir la lista

reloj :: [Integer]

cuyos elementos son los términos de la sucesión anterior. Por ejemplo,

λ> take 11 reloj
[1,2,3,4,32,123,43,2123,432,1234,32123]

Nota: La relación entre la sucesión y el funcionamiento del reloj se puede ver en The Mathematics Behind Prague's Horloge Introduction.

Sucesiones de listas de números

José A. Alonso

20-05-2016

Misceláneas

Particiones de longitud fija

José A. Alonso

19-05-2016

Misceláneas

Definir la función

particionesFijas :: Int -> Int -> [[Int]]

tal que (particionesFijas n k) es la lista de listas de k números naturales no crecientes cuya suma es n. Por ejemplo,

λ> particionesFijas 8 2
[[4,4],[5,3],[6,2],[7,1]]
λ> particionesFijas 8 3
[[3,3,2],[4,2,2],[4,3,1],[5,2,1],[6,1,1]]
λ> particionesFijas 9 3
[[3,3,3],[4,3,2],[4,4,1],[5,2,2],[5,3,1],[6,2,1],[7,1,1]]
λ> length (particionesFijas 67 5)
8056

Problema de las jarras

José A. Alonso

18-05-2016

Misceláneas

En el problema de las jarras (A,B,C) se tienen dos jarras sin marcas de medición, una de A litros de capacidad y otra de B. También se dispone de una bomba que permite llenar las jarras de agua.

El problema de las jarras (A,B,C) consiste en determinar cómo se puede lograr tener exactamente C litros de agua en la jarra de A litros de capacidad.

Definir, mediante búsqueda en espacio de estados, la función

jarras :: (Int,Int,Int) -> [[(Int,Int)]]

tal (jarras (a,b,c)) es la lista de las soluciones del problema de las jarras (a,b,c). Por ejemplo,

λ> take 2 (map snd (sort [(length xs,xs) | xs <- jarras (4,3,2)]))
[[(0,0),(0,3),(3,0),(3,3),(4,2),(0,2),(2,0)],
 [(0,0),(4,0),(1,3),(1,0),(0,1),(4,1),(2,3)]]

La interpretación [(0,0),(4,0),(1,3),(1,0),(0,1),(4,1),(2,3)] es:

(0,0) se inicia con las dos jarras vacías,
(4,0) se llena la jarra de 4 con el grifo,
(1,3) se llena la de 3 con la de 4,
(1,0) se vacía la de 3,
(0,1) se pasa el contenido de la primera a la segunda,
(4,1) se llena la primera con el grifo,
(2,3) se llena la segunda con la primera.

Otros ejemplos

λ> (snd . head . sort) [(length xs,xs) | xs <- jarras (15,10,5)]
[(0,0),(15,0),(5,10)]
λ> jarras (15,10,4)
[]

Nota: Las librerías necesarias se encuentran en la página de códigos.

Problema del dominó

José A. Alonso

17-05-2016

Misceláneas

Las fichas del dominó se pueden representar por pares de números enteros. El problema del dominó consiste en colocar todas las fichas de una lista dada de forma que el segundo número de cada ficha coincida con el primero de la siguiente.

Definir, mediante búsqueda en espacio de estados, la función

domino :: [(Int,Int)] -> [[(Int,Int)]]

tal que (domino fs) es la lista de las soluciones del problema del dominó correspondiente a las fichas fs. Por ejemplo,

λ> domino [(1,2),(2,3),(1,4)]
[[(4,1),(1,2),(2,3)],[(3,2),(2,1),(1,4)]]
λ> domino [(1,2),(1,1),(1,4)]
[[(4,1),(1,1),(1,2)],[(2,1),(1,1),(1,4)]]
λ> domino [(1,2),(3,4),(2,3)]
[[(1,2),(2,3),(3,4)]]
λ> domino [(1,2),(2,3),(5,4)]
[]
λ> domino [(x,y) | x <- [1..2], y <- [x..2]]
[[(2,2),(2,1),(1,1)],[(1,1),(1,2),(2,2)]]
λ> [(x,y) | x <- [1..3], y <- [x..3]]
[(1,1),(1,2),(1,3),(2,2),(2,3),(3,3)]
λ> mapM_ print (domino [(x,y) | x <- [1..3], y <- [x..3]])
[(1,3),(3,3),(3,2),(2,2),(2,1),(1,1)]
[(1,2),(2,2),(2,3),(3,3),(3,1),(1,1)]
[(2,2),(2,3),(3,3),(3,1),(1,1),(1,2)]
[(3,3),(3,2),(2,2),(2,1),(1,1),(1,3)]
[(2,3),(3,3),(3,1),(1,1),(1,2),(2,2)]
[(2,1),(1,1),(1,3),(3,3),(3,2),(2,2)]
[(3,3),(3,1),(1,1),(1,2),(2,2),(2,3)]
[(3,2),(2,2),(2,1),(1,1),(1,3),(3,3)]
[(3,1),(1,1),(1,2),(2,2),(2,3),(3,3)]
λ> length (domino [(x,y) | x <- [1..4], y <- [x..4]])
0

Nota: Las librerías necesarias se encuentran en la página de códigos.

Sucesión duplicadora

José A. Alonso

16-05-2016

Misceláneas

Para cada entero positivo n, existe una única sucesión que empieza en 1, termina en n y en la que cada uno de sus elementos es el doble de su anterior o el doble más uno. Dicha sucesión se llama la sucesión duplicadora de n. Por ejemplo, la sucesión duplicadora de 13 es [1, 3, 6, 13], ya que

 3 = 2*1 +1
 6 = 2*3
13 = 2*6 +1

Definir la función

duplicadora :: Integer -> [Integer]

tal que (duplicadora n) es la sucesión duplicadora de n. Por ejemplo,

duplicadora 13                   ==  [1,3,6,13]
duplicadora 17                   ==  [1,2,4,8,17]
length (duplicadora (10^40000))  ==  132878

Problema de las puertas

José A. Alonso

13-05-2016

Misceláneas

Un hotel dispone de n habitaciones y n camareros. Los camareros tienen la costumbre de cambiar de estado las puestas (es decir, abrir las cerradas y cerrar las abiertas). El proceso es el siguiente:

Inicialmente todas las puertas están cerradas.
El primer camarero cambia de estado las puertas de todas las habitaciones.
El segundo cambia de estado de las puertas de las habitaciones pares.
El tercero cambia de estado todas las puertas que son múltiplos de 3.
El cuarto cambia de estado todas las puertas que son múltiplos de 4
Así, hasta que ha pasado el último camarero.

Por ejemplo, para n = 5

Pase    | Puerta 1 | Puerta 2 | Puerta 3 | Puerta 4 | Puerta 5
Inicial | Cerrada  | Cerrada  | Cerrada  | Cerrada  | Cerrada
Pase 1  | Abierta  | Abierta  | Abierta  | Abierta  | Abierta
Pase 2  | Abierta  | Cerrada  | Abierta  | Cerrada  | Abierta
Pase 3  | Abierta  | Cerrada  | Cerrada  | Cerrada  | Abierta
Pase 4  | Abierta  | Cerrada  | Cerrada  | Abierta  | Abierta
Pase 5  | Abierta  | Cerrada  | Cerrada  | Abierta  | Cerrada

Los estados de las puertas se representan por el siguiente tipo de datos

data Estado = Abierta | Cerrada
              deriving (Eq, Show)

Definir la función

final :: Int -> [Estado]

tal que (final n) es la lista de los estados de las n puertas después de que hayan pasado los n camareros. Por ejemplo,

λ> final 5
[Abierta,Cerrada,Cerrada,Abierta,Cerrada]
λ> final 7
[Abierta,Cerrada,Cerrada,Abierta,Cerrada,Cerrada,Cerrada]

Juego de bloques con letras

José A. Alonso

12-05-2016

Misceláneas

Para el juego de los bloques se dispone de un conjunto de bloques con una letra en cada una de sus dos caras. El objetivo del juego consiste en formar palabras sin que se pueda usar un bloque más de una vez y sin diferenciar mayúsculas de minúsculas. Por ejemplo, si se tiene tres bloques de forma que el 1º tiene las letras A y B, el 2ª la N y la O y el 3º la O y la A entonces se puede obtener la palabra ANA de dos formas: una con los bloques 1, 2 y 3 y otra con los 3, 2 y 1.

Definir la función

soluciones :: [String] -> String -> [[String]]

tal que (soluciones bs cs) es la lista de las soluciones del juego de los bloque usando los bloques bs (cada bloque es una cadena de dos letras mayúsculas) para formar la palabra cs. Por ejemplo,

λ> soluciones ["AB","NO","OA"] "ANA"
[["AB","NO","OA"],["OA","NO","AB"]]
λ> soluciones ["AB","NE","OA"] "Bea"
[["AB","NE","OA"]]
λ> soluciones ["AB","NE","OA"] "EvA"
[]
λ> soluciones ["AB","NO","OA","NC"] "ANA"
[["AB","NO","OA"],["AB","NC","OA"],["OA","NO","AB"],["OA","NC","AB"]]
λ> soluciones ["AB","NO","OA","NC"] "Anca"
[["AB","NO","NC","OA"],["OA","NO","NC","AB"]]
λ> soluciones (["AB","NO","OA"] ++ replicate (10^6) "PQ") "ANA"
[["AB","NO","OA"],["OA","NO","AB"]]

Densidad de números no monótonos

José A. Alonso

11-05-2016

Misceláneas

Un número entero positivo se dice que es

creciente si cada uno de sus dígitos es menor o igual que el que está a su derecha; por ejemplo, 134479.
decreciente si cada uno de sus dígitos es menor o igual que el que está a su derecha; por ejemplo, 664210.
no monótono si no es creciente ni decreciente; por ejemplo, 155369.

Para cada entero positivo n, la densidad números no monótonos hasta n es el cociente entre la cantidad de n números no monótonos entre menores o iguales que n y el número n. Por ejemplo, hasta 150 hay 19 números no monótonos (101, 102, 103, 104, 105, 106, 107, 108, 109, 120, 121, 130, 131, 132, 140, 141, 142, 143 y 150); por tanto, la densidad hasta 150 es 19/150 = 0.12666667

Definir las siguientes funciones

densidad              :: Integer -> Float
menorConDensidadMayor :: Float -> Integer

tales que

(densidad n) es la densidad de números no monótonos hasta n. Por ejemplo,

densidad 100  ==  0.0
densidad 200  ==  0.265
densidad 400  ==  0.4375
densidad 800  ==  0.53375

(menorConDensidadMayor x) es el menor número n tal que la densidad de números no monótonos hasta n es mayor o igual que x. Por ejemplo,

menorConDensidadMayor 0.5   ==  538
densidad 537                ==  0.49906892
densidad 538                ==  0.5
menorConDensidadMayor 0.9   ==  21780
densidad 21779              ==  0.8999954
densidad 21780              ==  0.9
menorConDensidadMayor 0.99  ==  1586996

Sucesión fractal

José A. Alonso

10-05-2016

Misceláneas

La sucesión fractal

0, 0, 1, 0, 2, 1, 3, 0, 4, 2, 5, 1, 6, 3, 7, 0, 8, 4, 9, 2,
10, 5, 11, 1, 12, 6, 13, 3, 14, 7, 15, ...

está construida de la siguiente forma:

los términos pares forman la sucesión de los números naturales

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ...

los términos impares forman la misma sucesión original

0, 0, 1, 0, 2, 1, 3, 0, 4, 2, 5, 1, 6, 3, 7, ...

Definir las funciones

sucFractal     :: [Integer]
sumaSucFractal :: Integer -> Integer

tales que

sucFractal es la lista de los términos de la sucesión fractal. Por ejemplo,

take 20 sucFractal   == [0,0,1,0,2,1,3,0,4,2,5,1,6,3,7,0,8,4,9,2]
sucFractal !! 30     == 15
sucFractal !! (10^7) == 5000000

(sumaSucFractal n) es la suma de los n primeros términos de la sucesión fractal. Por ejemplo,

sumaSucFractal 10      == 13
sumaSucFractal (10^5)  == 1666617368
sumaSucFractal (10^10) == 16666666661668691669
sumaSucFractal (10^15) == 166666666666666166673722792954
sumaSucFractal (10^20) == 1666666666666666666616666684103392376198
length (show (sumaSucFractal (10^15000))) == 30000
sumaSucFractal (10^15000) `mod` (10^9)    == 455972157

Conjuntos de primos emparejables

José A. Alonso

09-05-2016

Misceláneas

Un conjunto de primos emparejables es un conjunto S de números primos tales que al concatenar cualquier par de elementos de S se obtiene un número primo. Por ejemplo, {3, 7, 109, 673} es un conjunto de primos emparejables ya que sus elementos son primos y las concatenaciones de sus parejas son 37, 3109, 3673, 73, 7109, 7673, 1093, 1097, 109673, 6733, 6737 y 673109 son primos.

Definir la función

emparejables :: Integer -> Integer -> [[Integer]]

tal que (emparejables n m) es el conjunto de los conjuntos emparejables de n elementos menores que n. Por ejemplo,

take 5 (emparejables 2   10)  ==  [[3,7]]
take 5 (emparejables 3   10)  ==  []
take 5 (emparejables 2  100)  ==  [[3,7],[3,11],[3,17],[3,31],[3,37]]
take 5 (emparejables 3  100)  ==  [[3,37,67],[7,19,97]]
take 5 (emparejables 4  100)  ==  []
take 5 (emparejables 4 1000)  ==  [[3,7,109,673],[23,311,677,827]]

Cadenas de divisores

José A. Alonso

06-05-2016

Misceláneas

Una cadena de divisores de un número n es una lista donde cada elemento es un divisor de su siguiente elemento en la lista. Por ejemplo, las cadenas de divisores de 12 son [2,4,12], [2,6,12], [2,12], [3,6,12], [3,12], [4,12], [6,12] y [12].

Definir la función

cadenasDivisores :: Int -> [[Int]]

tal que (cadenasDivisores n) es la lista de las cadenas de divisores de n. Por ejemplo,

λ> cadenasDivisores 12
[[2,4,12],[2,6,12],[2,12],[3,6,12],[3,12],[4,12],[6,12],[12]]
λ> length (cadenaDivisores 48)
48
λ> length (cadenaDivisores 120)
132

Número de divisiones en el algoritmo de Euclides

José A. Alonso

05-05-2016

Misceláneas

Dados dos números naturales, a y b, es posible calcular su máximo común divisor mediante el Algoritmo de Euclides. Este algoritmo se puede resumir en la siguiente fórmula:

mcd(a,b) = a,                   si b = 0
         = b,                   si a = 0
         = mcd (a módulo b, b), si a > b
         = mcd (a, b módulo a), si b >= a

Definir la función

mcdYdivisiones :: Int -> Int -> (Int,Int)

tal que (mcdYdivisiones a b) es el número de divisiones usadas en el cálculo del máximo común divisor de a y b mediante el algoritmo de Euclides. Por ejemplo,

mcdYdivisiones 252 198 == (18,4)

ya que los 4 divisiones del cálculo son

  mcd 252 198
= mcd  54 198
= mcd  54  36
= mcd  18  36
= mcd  18   0

Comprobar con QuickCheck que el número de divisiones requeridas por el algoritmo de Euclides para calcular el MCD de a y b es igual o menor que cinco veces el número de dígitos de menor de los números a y b.

Período de una lista

José A. Alonso

04-05-2016

Misceláneas

El período de una lista xs es la lista más corta ys tal que xs se puede obtener concatenando varias veces la lista ys. Por ejemplo, el período "abababab" es "ab" ya que "abababab" se obtiene repitiendo tres veces la lista "ab".

Definir la función

periodo :: Eq a => [a] -> [a]

tal que (periodo xs) es el período de xs. Por ejemplo,

periodo "ababab"      ==  "ab"
periodo "buenobueno"  ==  "bueno"
periodo "oooooo"      ==  "o"
periodo "sevilla"     ==  "sevilla"

Mezcla de infinitas listas infinitas

José A. Alonso

03-05-2016

Misceláneas

Definir la función

mezclaTodas :: Ord a => [[a]] -> [a]

tal que (mezclaTodas xss) es la mezcla ordenada de xss, donde tanto xss como sus elementos son listas infinitas ordenadas. Por ejemplo,

λ> take 10 (mezclaTodas [[n,2*n..] | n <- [2..]])
[2,3,4,5,6,7,8,9,10,11]
λ> take 10 (mezclaTodas [[n,2*n..] | n <- [2,9..]])
[2,4,6,8,9,10,12,14,16,18]

Expresiones aritmética normalizadas

José A. Alonso

02-05-2016

Misceláneas

El siguiente tipo de dato representa expresiones construidas con variables, sumas y productos

data Expr = Var String
          | S Expr Expr
          | P Expr Expre

Por ejemplo, x.(y+z) se representa por (P (V "x") (S (V "y") (V "z")))

Una expresión es un término si es un producto de variables. Por ejemplo, x.(y.z) es un término pero x+(y.z) ni x.(y+z) lo son.

Una expresión está en forma normal si es una suma de términos. Por ejemplo, x.(y,z) y x+(y.z) está en forma normal; pero x.(y+z) y (x+y).(x+z) no lo están.

Definir las funciones

esTermino, esNormal :: Expr -> Bool

tales que

(esTermino a) se verifica si a es un término. Por ejemplo,

esTermino (V "x")                                    == True
esTermino (P (V "x") (P (V "y") (V "z")))            == True
esTermino (P (V "x") (S (V "y") (V "z")))            == False
esTermino (S (V "x") (P (V "y") (V "z")))            == False

(esNormal a) se verifica si a está en forma normal. Por ejemplo,

esNormal (V "x")                                     == True
esNormal (P (V "x") (P (V "y") (V "z")))             == True
esNormal (S (V "x") (P (V "y") (V "z")))             == True
esNormal (P (V "x") (S (V "y") (V "z")))             == False
esNormal (P (S (V "x") (V "y")) (S (V "y") (V "z"))) == False

Operaciones con series de potencias

José A. Alonso

29-04-2016

Misceláneas

Una serie de potencias es una serie de la forma

a₀ + a₁x + a₂x² + a₃x³ + ...

Las series de potencias se pueden representar mediante listas infinitas. Por ejemplo, la serie de la función exponencial es

e^x = 1 + x + x²/2! + x³/3! + ...

y se puede representar por [1, 1, 1/2, 1/6, 1/24, 1/120, ...]

Las operaciones con series se pueden ver como una generalización de las de los polinomios.

En lo que sigue, usaremos el tipo (Serie a) para representar las series de potencias con coeficientes en a y su definición es

type Serie a = [a]

Definir las siguientes funciones

opuesta      :: Num a => Serie a -> Serie a
suma         :: Num a => Serie a -> Serie a -> Serie a
resta        :: Num a => Serie a -> Serie a -> Serie a
producto     :: Num a => Serie a -> Serie a -> Serie a
cociente     :: Fractional a => Serie a -> Serie a -> Serie a
derivada     :: (Num a, Enum a) => Serie a -> Serie a
integral     :: (Fractional a, Enum a) => Serie a -> Serie a
expx         :: Serie Rational

tales que

(opuesta xs) es la opuesta de la serie xs. Por ejemplo,

λ> take 7 (opuesta [-6,-4..])
[6,4,2,0,-2,-4,-6]

(suma xs ys) es la suma de las series xs e ys. Por ejemplo,

λ> take 7 (suma [1,3..] [2,4..])
[3,7,11,15,19,23,27]

(resta xs ys) es la resta de las series xs es ys. Por ejemplo,

λ> take 7 (resta [3,5..] [2,4..])
[1,1,1,1,1,1,1]
λ> take 7 (resta ([3,7,11,15,19,23,27] ++ repeat 0) [1,3..])
[2,4,6,8,10,12,14]

(producto xs ys) es el producto de las series xs e ys. Por ejemplo,

λ> take 7 (producto [3,5..] [2,4..])
[6,22,52,100,170,266,392]

(cociente xs ys) es el cociente de las series xs e ys. Por ejemplo,

λ> take 7 (cociente ([6,22,52,100,170,266,392] ++ repeat 0) [3,5..])
[2.0,4.0,6.0,8.0,10.0,12.0,14.0]

(derivada xs) es la derivada de la serie xs. Por ejemplo,

λ> take 7 (derivada [2,4..])
[4,12,24,40,60,84,112]

(integral xs) es la integral de la serie xs. Por ejemplo,

λ> take 7 (integral ([4,12,24,40,60,84,112] ++ repeat 0))
[0.0,4.0,6.0,8.0,10.0,12.0,14.0]

expx es la serie de la función exponencial. Por ejemplo,

λ> take 8 expx
[1 % 1,1 % 1,1 % 2,1 % 6,1 % 24,1 % 120,1 % 720,1 % 5040]
λ> take 8 (derivada expx)
[1 % 1,1 % 1,1 % 2,1 % 6,1 % 24,1 % 120,1 % 720,1 % 5040]
λ> take 8 (integral expx)
[0 % 1,1 % 1,1 % 2,1 % 6,1 % 24,1 % 120,1 % 720,1 % 5040]

Pandigitales primos

José A. Alonso

28-04-2016

Misceláneas

Un número con n dígitos es pandigital si contiene todos los dígitos del 1 a n exactamente una vez. Por ejemplo, 2143 es un pandigital con 4 dígitos y, además, es primo.

Definir la constante

pandigitalesPrimos :: [Int]

tal que sus elementos son los números pandigitales, ordenados de mayor a menor. Por ejemplo,

take 3 pandigitalesPrimos       ==  [7652413,7642513,7641253]
2143 `elem` pandigitalesPrimos  ==  True
length pandigitalesPrimos       ==  538

Mínimo número de cambios para igualar una lista

José A. Alonso

27-04-2016

Misceláneas

Definir la función

nMinimoCambios :: Ord a => [a] -> Int

tal que (nMinimoCambios xs) es el menor número de elementos de xs que hay que cambiar para que todos sean iguales. Por ejemplo,

nMinimoCambios [3,5,3,7,9,6]      ==  4
nMinimoCambios [3,5,3,7,3,3]      ==  2
nMinimoCambios "Salamanca"        ==  5
nMinimoCambios (4 : [1..500000])  ==  499999

En el primer ejemplo, los elementos que hay que cambiar son 5, 7, 9 y 6.

Numeración con múltiples bases

José A. Alonso

26-04-2016

Misceláneas

Sea \(\{b_i \mid i \geq 1\}\) una sucesión infinita de números enteros mayores que 1. Entonces, todo entero \(x\) mayor que cero se puede escribir de forma única como \[ x = x_0 + x_1 b_1 + x_2 b_1 b_2 + \dots + x_n b_1 b_2 \dotsm b_n, \] donde cada \(x_i\) satisface la condición \(0 \leq x_i < b_{i+1}\). Se dice que \([x_n, x_{n-1}, \dots, x_2, x_1, x_0]\) es la representación de \(x\) en la base \((b_i).

Por ejemplo, la representación de 377 en la base \((2i)_{i \geq 1}\) es \([7,5,0,1]\), ya que \[ 377 = 1 + 0 \times 2 + 5 \times 2 \times 4 + 7 \times 2 \times 4 \times 6, \] y además: \[ 0 \leq 1 < 2, \quad 0 \leq 0 < 4, \quad 0 \leq 5 < 6, \quad 0 \leq 7 < 8. \]

Definir las funciones

decimalAmultiple :: [Int] -> Int -> [Int]
multipleAdecimal :: [Int] -> [Int] -> Int

tales que (decimalAmultiple bs x) es la representación del número x en la base bs y (multipleAdecimal bs cs) es el número decimal cuya representación en la base bs es cs. Por ejemplo,

decimalAmultiple [2,4..] 377                      ==  [7,5,0,1]
multipleAdecimal [2,4..] [7,5,0,1]                ==  377
decimalAmultiple [2,5..] 377                      ==  [4,5,3,1]
multipleAdecimal [2,5..] [4,5,3,1]                ==  377
decimalAmultiple [2^n | n <- [1..]] 2015          ==  [1,15,3,3,1]
multipleAdecimal [2^n | n <- [1..]] [1,15,3,3,1]  ==  2015
decimalAmultiple (repeat 10) 2015                 ==  [2,0,1,5]
multipleAdecimal (repeat 10) [2,0,1,5]            ==  2015

Comprobar con QuickCheck que se verifican las siguientes propiedades

prop_inversas :: [Int] -> Int -> Property
prop_inversas bs x =
    x > 0 ==> multipleAdecimal bs (decimalAmultiple bs x) == x

prop_coeficientes :: [Int] -> Int -> Property
prop_coeficientes bs x =
    x > 0 ==> and [0 <= c && c < b | (c,b) <- zip cs bs]
    where cs = reverse (decimalAmultiple bs x)

para distintas bases dadas. Por ejemplo,

λ> quickCheck (prop_inversas [2,4..])
+++ OK, passed 100 tests.
λ> quickCheck (prop_inversas [3,5..])
+++ OK, passed 100 tests.
λ> quickCheck (prop_coeficientes [2,4..])
+++ OK, passed 100 tests.
λ> quickCheck (prop_coeficientes [3,5..])
+++ OK, passed 100 tests.

Productos simultáneos de dos y tres números consecutivos

José A. Alonso

25-04-2016

Misceláneas

Definir la función

productos :: Integer -> Integer -> [[Integer]]

tal que (productos n x) es las listas de n elementos consecutivos cuyo producto es x. Por ejemplo,

productos 2 6     ==  [[2,3]]
productos 3 6     ==  [[1,2,3]]
productos 4 1680  ==  [[5,6,7,8]]
productos 2 5     ==  []

Comprobar con QuickCheck que si n > 0 y x > 0, entonces

productos n (product [x..x+n-1]) == [[x..x+n-1]]

Usando productos, definir la función

productosDe2y3consecutivos :: [Integer]

cuyos elementos son los números naturales (no nulos) que pueden expresarse simultáneamente como producto de dos y tres números consecutivos. Por ejemplo,

head productosDe2y3consecutivos  ==  6

Nota. Según demostró Mordell en 1962, productosDe2y3consecutivos sólo tiene dos elementos.

Conflictos de horarios

José A. Alonso

22-04-2016

Misceláneas

Los horarios de los cursos se pueden representar mediante matrices donde las filas indican los curso, las columnas las horas de clase y el valor correspondiente al curso i y la hora j es verdadero indica que i tiene clase a la hora j.

En Haskell, podemos usar la matrices de la librería Data.Matrix y definir el tipo de los horarios por

type Horario = Matrix Bool

Un ejemplo de horario es

ejHorarios1 :: Horario
ejHorarios1 = fromLists [[True,  True,  False, False],
                         [False, True,  True,  False],
                         [False, False, True,  True]]

en el que el 1º curso tiene clase a la 1ª y 2ª hora, el 2º a la 2ª y a la 3ª y el 3º a la 3ª y a la 4ª.

Definir la función

cursosConflictivos :: Horario -> [Int] -> Bool

tal que (cursosConflictivos h is) se verifica para si los cursos de la lista is hay alguna hora en la que más de uno tiene clase a dicha hora. Por ejemplo,

cursosConflictivos ejHorarios1 [1,2]  ==  True
cursosConflictivos ejHorarios1 [1,3]  ==  False

Polinomios cuadráticos generadores de primos

José A. Alonso

21-04-2016

Misceláneas

En 1772, Euler publicó que el polinomio n² + n + 41 genera 40 números primos para todos los valores de n entre 0 y 39. Sin embargo, cuando n=40, 40²+40+41 = 40(40+1)+41 es divisible por 41.

Usando ordenadores, se descubrió el polinomio n² - 79n + 1601 que genera 80 números primos para todos los valores de n entre 0 y 79.

Definir la función

generadoresMaximales :: Integer -> (Int,[(Integer,Integer)])

tal que (generadoresMaximales n) es el par (m,xs) donde

xs es la lista de pares (x,y) tales que n²+xn+y es uno de los polinomios que genera un número máximo de números primos consecutivos a partir de cero entre todos los polinomios de la forma n²+an+b, con |a| ≤ n y |b| ≤ n y
m es dicho número máximo.

Por ejemplo,

generadoresMaximales    4  ==  ( 3,[(-2,3),(-1,3),(3,3)])
generadoresMaximales    6  ==  ( 5,[(-1,5),(5,5)])
generadoresMaximales   50  ==  (43,[(-5,47)])
generadoresMaximales  100  ==  (48,[(-15,97)])
generadoresMaximales  200  ==  (53,[(-25,197)])
generadoresMaximales 1650  ==  (80,[(-79,1601)])

Término ausente en una progresión aritmética

José A. Alonso

20-04-2016

Misceláneas

Una progresión aritmética es una sucesión de números tales que la diferencia de dos términos sucesivos cualesquiera de la sucesión es constante.

Definir la función

ausente :: Integral a => [a] -> a

tal que (ausente xs) es el único término ausente de la progresión aritmética xs. Por ejemplo,

ausente [3,7,9,11]                ==  5
ausente [3,5,9,11]                ==  7
ausente [3,5,7,11]                ==  9
ausente ([1..9]++[11..])          ==  10
ausente2 ([1..10^6] ++ [2+10^6])  ==  1000001

Nota. Se supone que la lista tiene al menos 3 elementos, que puede ser infinita y que sólo hay exactamente un término de la progresión aritmética que no está en la lista.

Matriz zigzagueante

José A. Alonso

19-04-2016

Misceláneas

La matriz zizagueante de orden n es la matriz cuadrada con n filas y n columnas y cuyos elementos son los n² primeros números naturales colocados de manera creciente a lo largo de las diagonales secundarias. Por ejemplo, La matriz zigzagueante de orden 5 es

 0  1  5  6 14
 2  4  7 13 15
 3  8 12 16 21
 9 11 17 20 22
10 18 19 23 24

La colocación de los elementos se puede ver gráficamente en Matriz zigzagueante

Definir la función

zigZag :: Int -> Array (Int,Int) Int

tal que (zigZag n) es la matriz zigzagueante de orden n. Por ejemplo,

λ> elems (zigZag 3)
[0,1,5, 2,4,6, 3,7,8]
λ> elems (zigZag 4)
[0,1,5,6, 2,4,7,12, 3,8,11,13, 9,10,14,15]
λ> elems (zigZag 5)
[0,1,5,6,14, 2,4,7,13,15, 3,8,12,16,21, 9,11,17,20,22, 10,18,19,23,24]
λ> take 15 (elems (zigZag 1000))
[0,1,5,6,14,15,27,28,44,45,65,66,90,91,119]

Mínima diferencia entre elementos de una lista

José A. Alonso

18-04-2016

Misceláneas

Definir la función

minimaDiferencia :: (Num a, Ord a) => [a] -> a

tal que (minimaDiferencia xs) es el menor valor absoluto de las diferencias entre todos los pares de elementos de xs (que se supone que tiene al menos 2 elementos). Por ejemplo,

minimaDiferencia [1,5,3,19,18,25]  ==  1
minimaDiferencia [30,5,20,9]       ==  4
minimaDiferencia [30,5,20,9,5]     ==  0
minimaDiferencia [1..10^6]         ==  1

En el primer ejemplo la menor diferencia es 1 y se da entre los elementos 19 y 18; en el 2ª es 4 entre los elementos 5 y 9 y en la 3ª es 0 porque el elemento 5 está repetido.

Números como sumas de primos consecutivos

José A. Alonso

15-04-2016

Misceláneas

En el artículo Integers as a sum of consecutive primes in 2,3,4,.. ways se presentan números que se pueden escribir como sumas de primos consecutivos de varias formas. Por ejemplo, el 41 se puede escribir de dos formas distintas

41 =  2 +  3 +  5 + 7 + 11 + 13
41 = 11 + 13 + 17

el 240 se puede escribir de tres formas

240 =  17 +  19 + 23 + 29 + 31 + 37 + 41 + 43
240 =  53 +  59 + 61 + 67
240 = 113 + 127

y el 311 se puede escribir de 4 formas

311 =  11 +  13 +  17 + 19 + 23 + 29 + 31 + 37 + 41 + 43 + 47
311 =  31 +  37 +  41 + 43 + 47 + 53 + 59
311 =  53 +  59 +  61 + 67 + 71
311 = 101 + 103 + 107

Definir la función

sumas :: Integer -> [[Integer]]

tal que (sumas x) es la lista de las formas de escribir x como suma de dos o más números primos consecutivos. Por ejemplo,

λ> sumas 41
[[2,3,5,7,11,13],[11,13,17]]
λ> sumas 240
[[17,19,23,29,31,37,41,43],[53,59,61,67],[113,127]]
λ> sumas 311
[[11,13,17,19,23,29,31,37,41,43,47],[31,37,41,43,47,53,59],[53,59,61,67,71],[101,103,107]]
λ> maximum [length (sumas n) | n <- [1..600]]
4

Suma de los elementos de las diagonales matrices espirales

José A. Alonso

14-04-2016

Misceláneas

Empezando con el número 1 y moviéndose en el sentido de las agujas del reloj se obtienen las matrices espirales

|1 2|   |7 8 9|   | 7  8  9 10|   |21 22 23 24 25|
|4 3|   |6 1 2|   | 6  1  2 11|   |20  7  8  9 10|
        |5 4 3|   | 5  4  3 12|   |19  6  1  2 11|
                  |16 15 14 13|   |18  5  4  3 12|
                                  |17 16 15 14 13|

La suma los elementos de sus diagonales es

en la 2x2: 1+3+2+4 = 10
en la 3x3: 1+3+5+7+9 = 25
en la 4x4: 1+2+3+4+7+10+13+16 = 56
en la 5x5: 1+3+5+7+9+13+17+21+25 = 101

Definir la función

sumaDiagonales :: Integer -> Integer

tal que (sumaDiagonales n) es la suma de los elementos en las diagonales de la matriz espiral de orden nxn. Por ejemplo.

sumaDiagonales 1         ==  1
sumaDiagonales 2         ==  10
sumaDiagonales 3         ==  25
sumaDiagonales 4         ==  56
sumaDiagonales 5         ==  101
sumaDiagonales (1+10^6)  ==  666669166671000001
sumaDiagonales (10^2)    ==         671800
sumaDiagonales (10^3)    ==        667168000
sumaDiagonales (10^4)    ==       666716680000
sumaDiagonales (10^5)    ==      666671666800000
sumaDiagonales (10^6)    ==     666667166668000000
sumaDiagonales (10^7)    ==    666666716666680000000
sumaDiagonales (10^8)    ==   666666671666666800000000
sumaDiagonales (10^9)    ==  666666667166666668000000000

Comprobar con QuickCheck que el último dígito de (sumaDiagonales n) es 0, 4 ó 6 si n es par y es 1, 5 ó 7 en caso contrario.

Descomposiciones con sumandos 1 ó 2

José A. Alonso

13-04-2016

Misceláneas

Definir la funciones

sumas  :: Int -> [[Int]]
nSumas :: Int -> Integer

tales que

(sumas n) es la lista de las descomposiciones de n como sumas cuyos sumandos son 1 ó 2. Por ejemplo,

sumas 1            ==  [[1]]
sumas 2            ==  [[1,1],[2]]
sumas 3            ==  [[1,1,1],[1,2],[2,1]]
sumas 4            ==  [[1,1,1,1],[1,1,2],[1,2,1],[2,1,1],[2,2]]
length (sumas 26)  ==  196418
length (sumas 33)  ==  5702887

(nSumas n) es el número de descomposiciones de n como sumas cuyos sumandos son 1 ó 2. Por ejemplo,

nSumas 4                      ==  5
nSumas 123                    ==  36726740705505779255899443
length (show (nSumas 123456)) ==  25801

Caminos reducidos

José A. Alonso

12-04-2016

Misceláneas

Un camino es una sucesión de pasos en una de las cuatros direcciones Norte, Sur, Este, Oeste. Ir en una dirección y a continuación en la opuesta es un esfuerzo que se puede reducir, Por ejemplo, el camino [Norte,Sur,Este,Sur] se puede reducir a [Este,Sur].

Un camino se dice que es reducido si no tiene dos pasos consecutivos en direcciones opuesta. Por ejemplo, [Este,Sur] es reducido y [Norte,Sur,Este,Sur] no lo es.

En Haskell, las direcciones y los caminos se pueden definir por

data Direccion = N | S | E | O deriving (Show, Eq)
type Camino = [Direccion]

Definir la función

reducido :: Camino -> Camino

tal que (reducido ds) es el camino reducido equivalente al camino ds. Por ejemplo,

reducido []                              ==  []
reducido [N]                             ==  [N]
reducido [N,O]                           ==  [N,O]
reducido [N,O,E]                         ==  [N]
reducido [N,O,E,S]                       ==  []
reducido [N,O,S,E]                       ==  [N,O,S,E]
reducido [S,S,S,N,N,N]                   ==  []
reducido [N,S,S,E,O,N]                   ==  []
reducido [N,S,S,E,O,N,O]                 ==  [O]
reducido (take (10^7) (cycle [N,E,O,S])) ==  []

Nótese que en el penúltimo ejemplo las reducciones son

    [N,S,S,E,O,N,O]
--> [S,E,O,N,O]
--> [S,N,O]
--> [O]

Primos permutables

José A. Alonso

11-04-2016

Misceláneas

Un primo permutable es un número primo tal que todos los números obtenidos permutando sus cifras son primos. Por ejemplo, 337 es un primo permutable ya que 337, 373 y 733 son primos.

Definir las funciones

esPrimoPermutable :: Integer -> Bool
primosPermutables :: [Integer]

tales que

(esPrimoPermutable x) se verifica si x es un primo permutable. Por ejemplo,

esPrimoPermutable 97  ==  True
esPrimoPermutable 337 ==  True
esPrimoPermutable 23  ==  False

primosPermutables es la lista de los primos permutables. Por ejemplo,

λ> take 20 primosPermutables
[2,3,5,7,11,13,17,31,37,71,73,79,97,113,131,199,311,337,373,733]