La codificación de Fibonacci de un número n es una cadena d = d(0)d(1)...d(k-1)d(k) de ceros y unos tal que

n = d(0)·F(2) + d(1)·F(3) +...+ d(k-1)·F(k+1)
d(k-1) = d(k) = 1

donde F(i) es el i-ésimo término de la sucesión de Fibonacci

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Por ejemplo, la codificación de Fibonacci de 4 es "1011" ya que los dos últimos elementos son iguales a 1 y

1·F(2) + 0·F(3) + 1·F(4) = 1·1 + 0·2 + 1·3 = 4

La codificación de Fibonacci de los primeros números se muestra en la siguiente tabla

 1  = 1     = F(2)           ≡       11
 2  = 2     = F(3)           ≡      011
 3  = 3     = F(4)           ≡     0011
 4  = 1+3   = F(2)+F(4)      ≡     1011
 5  = 5     = F(5)           ≡    00011
 6  = 1+5   = F(2)+F(5)      ≡    10011
 7  = 2+5   = F(3)+F(5)      ≡    01011
 8  = 8     = F(6)           ≡   000011
 9  = 1+8   = F(2)+F(6)      ≡   100011
10  = 2+8   = F(3)+F(6)      ≡   010011
11  = 3+8   = F(4)+F(6)      ≡   001011
12  = 1+3+8 = F(2)+F(4)+F(6) ≡   101011
13  = 13    = F(7)           ≡  0000011
14  = 1+13  = F(2)+F(7)      ≡  1000011

Definir la función

codigoFib :: Integer -> String

tal que (codigoFib n) es la codificación de Fibonacci del número n. Por ejemplo,

λ> codigoFib 65
"0100100011"
λ> [codigoFib n | n <- [1..7]]
["11","011","0011","1011","00011","10011","01011"]

Comprobar con QuickCheck las siguientes propiedades:

• Todo entero positivo se puede descomponer en suma de números de la sucesión de Fibonacci.
• Las codificaciones de Fibonacci tienen como mínimo 2 elementos.
• En las codificaciones de Fibonacci, la cadena "11" sólo aparece una vez y la única vez que aparece es al final.

Leer más…

La cadena infinita "1234321234321234321...", formada por la repetición de los dígitos 123432, tiene una propiedad (en la que se basa el funcionamiento del reloj astronómico de Praga: la cadena se puede partir en una sucesión de números, de forma que la suma de los dígitos de dichos números es la sucesión de los números naturales, como se observa a continuación:

1, 2, 3, 4, 32, 123, 43, 2123, 432, 1234, 32123, ...
1, 2, 3, 4,  5,   6,  7,    8,   9,   10,    11, ...

Definir la lista

reloj :: [Integer]

cuyos elementos son los términos de la sucesión anterior. Por ejemplo,

λ> take 11 reloj
[1,2,3,4,32,123,43,2123,432,1234,32123]
λ> (reloj !! 1000) `mod` (10^50)
23432123432123432123432123432123432123432123432123

Nota: La relación entre la sucesión y el funcionamiento del reloj se puede ver en The Mathematics Behind Prague's Horloge Introduction.

Leer más…

El método de bisección para calcular un cero de una función en el intervalo [a,b] se basa en el teorema de Bolzano:

"Si f(x) es una función continua en el intervalo [a, b], y si, además, en los extremos del intervalo la función f(x) toma valores de signo opuesto (f(a) * f(b) < 0), entonces existe al menos un valor c en (a, b) para el que f(c) = 0".

El método para calcular un cero de la función f en el intervalo [a,b] con un error menor que e consiste en tomar el punto medio del intervalo c = (a+b)/2 y considerar los siguientes casos:

• Si |f(c)| < e, hemos encontrado una aproximación del punto que anula f en el intervalo con un error aceptable.
• Si f(c) tiene signo distinto de f(a), repetir el proceso en el intervalo [a,c].
• Si no, repetir el proceso en el intervalo [c,b].

Definir la función

biseccion :: (Double -> Double) -> Double -> Double -> Double -> Double

tal que (biseccion f a b e) es una aproximación del punto del intervalo [a,b] en el que se anula la función f, con un error menor que e, calculada mediante el método de la bisección. Por ejemplo,

biseccion (\x -> x^2 - 3) 0 5 0.01             ==  1.7333984375
biseccion (\x -> x^3 - x - 2) 0 4 0.01         ==  1.521484375
biseccion cos 0 2 0.01                         ==  1.5625
biseccion (\x -> log (50-x) - 4) (-10) 3 0.01  ==  -5.125

Leer más…

Un número n es especial si mcm(1,2,...,n-1) = mcm(1,2,...,n). Por ejemplo, el 6 es especial ya que

mcm(1,2,3,4,5) = 60 = mcm(1,2,3,4,5,6)

Definir la sucesión

especiales :: [Integer]

cuyos términos son los números especiales. Por ejemplo,

take 10 especiales     ==  [1,6,10,12,14,15,18,20,21,22]
especiales !! 50       ==  84
especiales !! 500      ==  638
especiales !! 5000     ==  5806
especiales !! 50000    ==  55746

Leer más…

Definir la función

suma :: Integer -> Integer

tal que (suma n) es la suma 1·1! + 2·2! + 3·3! + ... + n·n!. Por ejemplo,

suma 1  ==  1
suma 2  ==  5
suma 3  ==  23
suma 4  ==  119
suma 5  ==  719
take 9 (show (suma 70000))  ==  "823780458"

Leer más…

La integral definida de una función f entre los límites a y b puede calcularse mediante la regla del rectángulo usando la fórmula \[ h \cdot \left( f\left(a + \frac{h}{2}\right) + f\left(a + h + \frac{h}{2}\right) + f\left(a + 2h + \frac{h}{2}\right) + \dots + f\left(a + nh + \frac{h}{2}\right) \right) \] con \[ a + n h + \frac{h}{2} \leq b < a + (n+1) h + \frac{h}{2} \] y usando valores pequeños para \(h\).

Definir la función

integral :: (Fractional a, Ord a) => a -> a -> (a -> a) -> a -> a

tal que (integral a b f h) es el valor de dicha expresión. Por ejemplo, el cálculo de la integral de f(x) = x^3 entre 0 y 1, con paso 0.01, es

integral 0 1 (^3) 0.01  ==  0.24998750000000042

Otros ejemplos son

integral 0 1 (^4) 0.01                   ==  0.19998333362500048
integral 0 1 (\x -> 3*x^2 + 4*x^3) 0.01  ==  1.9999250000000026
log 2 - integral 1 2 (\x -> 1/x) 0.01         ==  3.124931644782336e-6
pi - 4 * integral 0 1 (\x -> 1/(x^2+1)) 0.01  ==  -8.333333331389525e-6

Leer más…

El menor número con 2 divisores es el 2, ya que tiene 2 divisores (el 1 y el 2) y el anterior al 2 (el 1) sólo tiene 1 divisor (el 1).

El menor número con 4 divisores es el 6, ya que tiene 4 divisores (el 1, 2, 3 y 6) y sus anteriores (el 1, 2, 3, 4 y 5) tienen menos de 4 divisores (tienen 1, 1, 1, 3 y 1, respectivamente).

El menor número con 8 divisores es el 24, ya que tiene 8 divisores (el 1, 2, 3, 4, 6, 8, 12 y 24) y sus anteriores (del 1 al 23) tienen menos de 8 divisores.

El menor número con 16 divisores es el 120, ya que tiene 16 divisores (el 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 y 120) y sus anteriores (del 1 al 119) tienen menos de 16 divisores.

Definir la función

menor :: Integer -> Integer

tal que (menor n) es el menor número con 2^n divisores. Por ejemplo,

menor 1  ==  2
menor 2  ==  6
menor 3  ==  24
menor 4  ==  120
length (show (menor (4*10^4)))  ==  207945

Comprobar con QuickCheck que, para todo k >=0, (menor (2^k)) es un divisor de (menor (2^(k+1))).

Nota: Este ejercicio está basado en el problema N1 de la Olimpíada Internacional de Matemáticas (IMO) del 2011.

Leer más…

Definir, por simulación, la función

distanciaEsperada :: Int -> IO Double

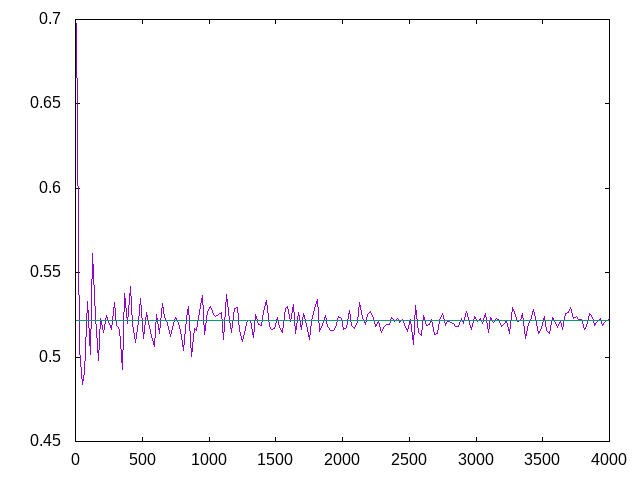
tal que (distanciaEsperada n) es la distancia esperada entre n puntos del cuadrado unitario de vértices opuestos (0,0) y (1,1), elegidos aleatoriamente. Por ejemplo,

distanciaEsperada 10     ==  0.43903617921423593
distanciaEsperada 10     ==  0.6342350621260004
distanciaEsperada 100    ==  0.5180418995364429
distanciaEsperada 100    ==  0.5288261085653962
distanciaEsperada 1000   ==  0.5143804432569616
distanciaEsperada 10000  ==  0.5208360147922616

El valor exacto de la distancia esperada es \[ ve = \frac{\sqrt{2} + 2 + 5 \log(1 + \sqrt{2})}{15} \approx 0.5214054331647207 \]

Definir la función

graficaDistanciaEsperada :: [Int] -> IO ()

tal que (graficaDistanciaEsperada ns) dibuja las gráficas de los pares (n, distanciaEsperada n) para n en la lista creciente ns junto con la recta y = ve, donde ve es el valor exacto. Por ejemplo, (graficaDistanciaEsperada [10,30..4000]) dibuja

Leer más…

Dada una relación r sobre un conjunto de números enteros, la matriz asociada a r es una matriz booleana p (cuyos elementos son True o False), tal que p(i,j) = True si y sólo si i está relacionado con j mediante la relación r.

Las relaciones binarias homogéneas y las matrices booleanas se pueden representar por

type Relacion = ([Int],[(Int,Int)])
type Matriz = Array (Int,Int) Bool

Definir la función

matrizRB:: Relacion -> Matriz

tal que (matrizRB r) es la matriz booleana asociada a r. Por ejemplo,

λ> matrizRB ([1..3],[(1,1), (1,3), (3,1), (3,3)])
array ((1,1),(3,3)) [((1,1),True) ,((1,2),False),((1,3),True),
((2,1),False),((2,2),False),((2,3),False),
((3,1),True) ,((3,2),False),((3,3),True)]
λ> matrizRB ([1..3],[(1,3), (3,1)])
array ((1,1),(3,3)) [((1,1),False),((1,2),False),((1,3),True),
((2,1),False),((2,2),False),((2,3),False),
((3,1),True) ,((3,2),False),((3,3),False)]
λ> let n = 10^4 in matrizRB3 ([1..n],[(1,n),(n,1)]) ! (n,n)
False

Leer más…

Dada una lista de números naturales xs, codificación de Gödel de xs se obtiene multiplicando las potencias de los primos sucesivos, siendo los exponentes los sucesores de los elementos de xs. Por ejemplo, si xs = [6,0,4], la codificación de xs es \[2^7 \times 3^1 \times 5^5 = 1200000 \]

Definir las funciones

codificaG   :: [Integer] -> Integer
decodificaG :: Integer -> [Integer]

tales que

• (codificaG xs) es la codificación de Gödel de xs. Por ejemplo,

codificaG [6,0,4]            ==  1200000
codificaG [3,1,1]            ==  3600
codificaG [3,1,0,0,0,0,0,1]  ==  4423058640
codificaG [1..6]             ==  126111168580452537982500

• (decodificaG n) es la lista xs cuya codificación es n. Por ejemplo,

decodificaG 1200000                   ==  [6,0,4]
decodificaG 3600                      ==  [3,1,1]
decodificaG 4423058640                ==  [3,1,0,0,0,0,0,1]
decodificaG 126111168580452537982500  ==  [1,2,3,4,5,6]

Comprobar con QuickCheck que ambas funciones son inversas; es decir,

decodificaG (codificaG xs) = xs
codificaG (decodificaG n) = n

Leer más…

Un primo circular es un número tal que todas las rotaciones de dígitos producen números primos. Por ejemplo, 195 es un primo circular ya que las rotaciones de sus dígitos son 197, 971 y 719 y los tres números son primos.

Definir la lista

circulares :: [Integer]

cuyo valor es la lista de los números primos circulares. Por ejemplo,

take 16 circulares == [2,3,5,7,11,13,17,31,37,71,73,79,97,113,131,197]
circulares !! 50   == 933199

Leer más…

Definir la función

frecuencias :: Ord a => [a] -> Map a Int

tal que (frecuencias xs) es el diccionario formado por los elementos de xs junto con el número de veces que aparecen en xs. Por ejemplo,

λ> frecuencias "sosos"
fromList [('o',2),('s',3)]
λ> frecuencias (show (10^100))
fromList [('0',100),('1',1)]
λ> frecuencias (take (10^6) (cycle "abc"))
fromList [('a',333334),('b',333333),('c',333333)]
λ> size (frecuencias (take (10^6) (cycle [1..10^6])))
1000000

Leer más…

Definir la funciones

sumas  :: Int -> [[Int]]
nSumas :: Int -> Integer

tales que

• (sumas n) es la lista de las descomposiciones de n como sumas cuyos sumandos son 1 ó 2. Por ejemplo,

sumas 1            ==  [[1]]
sumas 2            ==  [[1,1],[2]]
sumas 3            ==  [[1,1,1],[1,2],[2,1]]
sumas 4            ==  [[1,1,1,1],[1,1,2],[1,2,1],[2,1,1],[2,2]]
length (sumas 26)  ==  196418
length (sumas 33)  ==  5702887

• (nSumas n) es el número de descomposiciones de n como sumas cuyos sumandos son 1 ó 2. Por ejemplo,

nSumas 4                      ==  5
nSumas 123                    ==  36726740705505779255899443
length (show (nSumas 123456)) ==  25801

Leer más…

Empezando con el número 1 y moviéndose en el sentido de las agujas del reloj se obtienen las matrices espirales

|1 2|   |7 8 9|   | 7  8  9 10|   |21 22 23 24 25|
|4 3|   |6 1 2|   | 6  1  2 11|   |20  7  8  9 10|
        |5 4 3|   | 5  4  3 12|   |19  6  1  2 11|
                  |16 15 14 13|   |18  5  4  3 12|
                                  |17 16 15 14 13|

La suma los elementos de sus diagonales es

+ en la 2x2: 1+3+2+4               =  10
+ en la 3x3: 1+3+5+7+9             =  25
+ en la 4x4: 1+2+3+4+7+10+13+16    =  56
+ en la 5x5: 1+3+5+7+9+13+17+21+25 = 101

Definir la función

sumaDiagonales :: Integer -> Integer

tal que (sumaDiagonales n) es la suma de los elementos en las diagonales de la matriz espiral de orden nxn. Por ejemplo.

sumaDiagonales 1         ==  1
sumaDiagonales 2         ==  10
sumaDiagonales 3         ==  25
sumaDiagonales 4         ==  56
sumaDiagonales 5         ==  101
sumaDiagonales (10^6)    ==  666667166668000000
sumaDiagonales (1+10^6)  ==  666669166671000001

sumaDiagonales (10^2)  ==         671800
sumaDiagonales (10^3)  ==        667168000
sumaDiagonales (10^4)  ==       666716680000
sumaDiagonales (10^5)  ==      666671666800000
sumaDiagonales (10^6)  ==     666667166668000000
sumaDiagonales (10^7)  ==    666666716666680000000
sumaDiagonales (10^8)  ==   666666671666666800000000
sumaDiagonales (10^9)  ==  666666667166666668000000000

Comprobar con QuickCheck que el último dígito de (sumaDiagonales n) es 0, 4 ó 6 si n es par y es 1, 5 ó 7 en caso contrario.

Leer más…

Una progresión aritmética es una sucesión de números tales que la diferencia de dos términos sucesivos cualesquiera de la sucesión es constante.

Definir la función

ausente :: Integral a => [a] -> a

tal que (ausente xs) es el único término ausente de la progresión aritmética xs. Por ejemplo,

ausente [3,7,9,11]               ==  5
ausente [3,5,9,11]               ==  7
ausente [3,5,7,11]               ==  9
ausente ([1..9]++[11..])         ==  10
ausente ([1..10^6] ++ [2+10^6])  ==  1000001

Nota. Se supone que la lista tiene al menos 3 elementos, que puede ser infinita y que sólo hay un término de la progresión aritmética que no está en la lista.

Leer más…

Los polinomios de Bell forman una sucesión de polinomios, definida como sigue:

• B₀(x) = 1 (polinomio unidad)
• Bₙ(x) = x·[Bₙ(x) + Bₙ'(x)] (donde Bₙ'(x) es la derivada de Bₙ(x))

Por ejemplo,

B₀(x) = 1                     = 1
B₁(x) = x·(1+0)               = x
B₂(x) = x·(x+1)               = x²+x
B₃(x) = x·(x²+x+2x+1)         = x³+3x²+x
B₄(x) = x·(x³+3x²+x+3x²+6x+1) = x⁴+6x³+7x²+x

Definir la función

polBell :: Integer -> Polinomio Integer

tal que (polBell n) es el polinomio de Bell de grado n. Por ejemplo,

polBell 4                    ==  x^4 + 6*x^3 + 7*x^2 + 1*x
coeficiente 2 (polBell 4)    ==  7
coeficiente 2 (polBell 30)   ==  536870911
coeficiente 1 (polBell 1000) == 1
length (show (coeficiente 9 (polBell 2000)))  ==  1903

Notas: Se usa la librería I1M.PolOperaciones. Además, en el último ejemplo se usa la función coeficiente tal que (coeficiente k p) es el coeficiente del término de grado k en el polinomio p definida por

coeficiente :: Num a => Int -> Polinomio a -> a
coeficiente k p | k == n                 = coefLider p
                | k > grado (restoPol p) = 0
                | otherwise              = coeficiente k (restoPol p)
                where n = grado p

Leer más…

En este ejercicio, representamos las fracciones mediante pares de números de enteros.

Definir la función

fraccionesOrd :: Integer -> [(Integer,Integer)]

tal que (fraccionesOrd n) es la lista con las fracciones propias positivas ordenadas, con denominador menor o igual que n. Por ejemplo,

λ> fraccionesOrd 4
[(1,4),(1,3),(1,2),(2,3),(3,4)]
λ> fraccionesOrd 5
[(1,5),(1,4),(1,3),(2,5),(1,2),(3,5),(2,3),(3,4),(4,5)]

Leer más…

En 1772, Euler publicó que el polinomio n² + n + 41 genera 40 números primos para todos los valores de n entre 0 y 39. Sin embargo, cuando n = 40, 40²+40+41 = 40(40+1)+41 es divisible por 41.

Usando ordenadores, se descubrió que el polinomio n² - 79n + 1601 genera 80 números primos para todos los valores de n entre 0 y 79.

Definir la función

generadoresMaximales :: Integer -> (Int,[(Integer,Integer)])

tal que (generadoresMaximales n) es el par (m,xs) donde

• xs es la lista de pares (x,y) tales que n²+xn+y es uno de polinomios que genera un número máximo de números primos consecutivos a partir de cero entre todos los polinomios de la forma n²+an+b, con |a| ≤ n y |b| ≤ n y
• m es dicho número máximo.

Por ejemplo,

generadoresMaximales    4  ==  ( 3,[(-2,3),(-1,3),(3,3)])
generadoresMaximales    6  ==  ( 5,[(-1,5),(5,5)])
generadoresMaximales   41  ==  (41,[(-1,41)])
generadoresMaximales   50  ==  (43,[(-5,47)])
generadoresMaximales  100  ==  (48,[(-15,97)])
generadoresMaximales  200  ==  (53,[(-25,197)])
generadoresMaximales 1650  ==  (80,[(-79,1601)])

Leer más…

El triángulo de Floyd, llamado así en honor a Robert Floyd, es un triángulo rectángulo formado con números naturales. Para crear un triángulo de Floyd, se comienza con un 1 en la esquina superior izquierda, y se continúa escribiendo la secuencia de los números naturales de manera que cada línea contenga un número más que la anterior. Las 5 primeras líneas del triángulo de Floyd son

 1
 2   3
 4   5   6
 7   8   9  10
11  12  13  14  15

Definir la función

trianguloFloyd :: [[Integer]]

tal que trianguloFloyd es el triángulo de Floyd. Por ejemplo,

λ> take 4 trianguloFloyd
[[1],
 [2,3],
 [4,5,6],
 [7,8,9,10]]

(trianguloFloyd !! (10^5)) !! 0  ==  5000050001
(trianguloFloyd !! (10^6)) !! 0  ==  500000500001
(trianguloFloyd !! (10^7)) !! 0  ==  50000005000001

Leer más…

Leer más…

La matriz zizagueante de orden n es la matriz cuadrada con n filas y n columnas y cuyos elementos son los n² primeros números naturales colocados de manera creciente a lo largo de las diagonales secundarias. Por ejemplo, La matriz zigzagueante de orden 5 es

 0  1  5  6 14
 2  4  7 13 15
 3  8 12 16 21
 9 11 17 20 22
10 18 19 23 24

La colocación de los elementos se puede ver gráficamente en este enlace.

Definir la función

zigZag :: Int -> Matrix Int

tal que (zigZag n) es la matriz zigzagueante de orden n. Por ejemplo,

λ> zigZag 5
┌                ┐
│  0  1  5  6 14 │
│  2  4  7 13 15 │
│  3  8 12 16 21 │
│  9 11 17 20 22 │
│ 10 18 19 23 24 │
└                ┘
λ> zigZag 4
┌             ┐
│  0  1  5  6 │
│  2  4  7 12 │
│  3  8 11 13 │
│  9 10 14 15 │
└             ┘
λ> maximum (zigZag 1500)
2249999

Leer más…

La n-ésima densidad de un tipo de número es el cociente entre la cantidad de los números entre 1 y n que son del tipo considerado y n. Por ejemplo, la 7-ésima densidad de los múltiplos de 3 es 2/7 ya que entre los 7 primeros números sólo 2 son múltiplos de 3.

Definir las funciones

densidades :: Int -> (Double,Double,Double)
graficas   :: Int -> IO ()

tales que

• (densidades n) es la terna formada por la n-ésima densidad de los números abundantes (es decir, para que la suma de sus divisores propios es mayor que el número), de los números perfectos (es decir, para los que la suma de sus divisores propios es mayor que el número) y de los números deficientes (es decir, para los que la suma de sus divisores propios es menor que el número). Por ejemplo,

densidades 100     ==  (0.22,    2.0e-2, 0.76)
densidades 1000    ==  (0.246,   3.0e-3, 0.751)
densidades 10000   ==  (0.2488,  4.0e-4, 0.7508)
densidades 100000  ==  (0.24795, 4.0e-5, 0.75201)
densidades 1000000 ==  (0.247545,4.0e-6, 0.752451)

• (graficas n) dibuja las gráficas de las k-ésimas densidades (para k entre 1 y n) de los números abundantes, de los números perfectos y de los números deficientes. Por ejemplo, (graficas 100) dibuja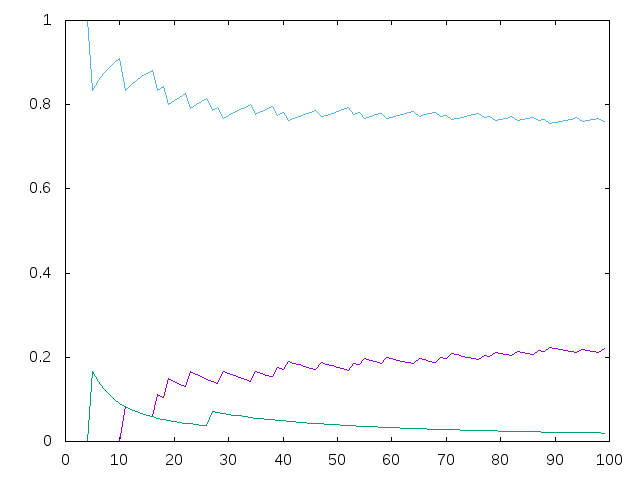

y (graficas 400) dibuja

Leer más…

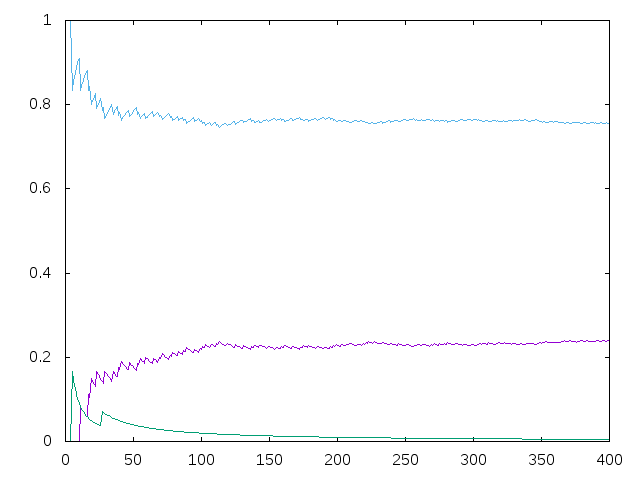
Definir la función

sumaDivisoresHasta :: Integer -> [(Integer,Integer)]

tal que (sumaDivisoresHasta n) es la lista de los pares (a,b) tales que a es un número entre 1 y n y b es la suma de los divisores propios de a. Por ejemplo,

λ> sumaDivisoresHasta 12
[(1,0),(2,1),(3,1),(4,3),(5,1),(6,6),(7,1),(8,7),(9,4),(10,8),(11,1),(12,16)]
λ> last (sumaDivisoresHasta2 (10^7))
(10000000,14902280)

Leer más…

Definir la función

divisoresHasta :: Int -> [(Int,Int)]

tal que (divisoresHasta n) es la lista de los pares (a,b) tales que a es un número entre 2 y n y b es un divisor propio de a. Por ejemplo,

λ> divisoresHasta 6
[(2,1),(3,1),(4,1),(5,1),(6,1),(4,2),(6,2),(6,3)]
λ> divisoresHasta 8
[(2,1),(3,1),(4,1),(5,1),(6,1),(7,1),(8,1),(4,2),(6,2),(8,2),(6,3),(8,4)]
λ> length (divisoresHasta 1234567)
16272448

Leer más…

La conjetura de Waring sobre los números primos establece que todo número impar es primo o la suma de tres primos. La conjetura de Goldbach afirma que todo par mayor que 2 es la suma de dos números primos. Ambos ha estado abiertos durante más de 200 años. En este problema no se propone su solución, sino una tarea más simple: buscar una manera de expresar los enteros mayores que 7 como suma de exactamente cuatro números primos; es decir, definir la función

suma4primos :: Integer -> [(Integer,Integer,Integer,Integer)]

tal que (suma4primos n) es la lista de las cuádruplas crecientes (a,b,c,d) de números primos cuya suma es n (que se supone mayor que 7). Por ejemplo,

suma4primos 18             == [(2,2,3,11),(2,2,7,7),(3,3,5,7),(3,5,5,5)]
head (suma4primos (10^14)) == (2,2,23,99999999999973)

Comprobar con QuickCheck que todo entero mayor que 7 se puede escribir como suma de exactamente cuatro números primos.

Leer más…

Un número n es abundante si la suma de los divisores propios de n es mayor que n. El primer número abundante es el 12 (cuyos divisores propios son 1, 2, 3, 4 y 6 cuya suma es 16). Por tanto, el menor número que es la suma de dos números abundantes es el 24.

Definir la sucesión

sumasDeDosAbundantes :: [Integer]

cuyos elementos son los números que se pueden escribir como suma de dos números abundantes. Por ejemplo,

take 10 sumasDeDosAbundantes  ==  [24,30,32,36,38,40,42,44,48,50]

Leer más…

Definir la función

sumaDivisores :: Integer -> Integer

tal que (sumaDivisores x) es la suma de los divisores de x. Por ejemplo,

sumaDivisores 12  ==  28
sumaDivisores 25  ==  31
sumaDivisores (product [1..25])  ==  93383273455325195473152000
length (show (sumaDivisores (product [1..30000])))  ==  121289
maximum (map sumaDivisores [1..10^5])  ==  403200

Leer más…

Definir la función

numeroDivisores :: Integer -> Integer

tal que (numeroDivisores x) es el número de divisores de x. Por ejemplo,

numeroDivisores 12  ==  6
numeroDivisores 25  ==  3
length (show (numeroDivisores (product [1..3*10^4])))  ==  1948

Leer más…

Definir la función

divisores :: Integer -> [Integer]

tal que (divisores x) es el conjunto de divisores de x. Por ejemplo,

divisores 30  ==  [1,2,3,5,6,10,15,30]
length (divisores (product [1..10]))  ==  270
length (divisores (product [1..25]))  ==  340032

Leer más…

Definir la función

esPotenciaDeDos :: Integer -> Bool

tal que (esPotenciaDeDos n) se verifica si n es una potencia de dos (suponiendo que n es mayor que 0). Por ejemplo.

esPotenciaDeDos    1        == True
esPotenciaDeDos    2        == True
esPotenciaDeDos    6        == False
esPotenciaDeDos    8        == True
esPotenciaDeDos 1024        == True
esPotenciaDeDos 1026        == False
esPotenciaDeDos (2^(10^8))  == True

Leer más…

Una [partición)(https://en.wikipedia.org/wiki/Integer_partition) de un entero positivo n es una manera de escribir n como una suma de enteros positivos. Dos sumas que sólo difieren en el orden de sus sumandos se consideran la misma partición. Por ejemplo, 4 tiene cinco particiones: 4, 3+1, 2+2, 2+1+1 y 1+1+1+1.

Definir la función

particiones :: Int -> [[Int]]

tal que (particiones n) es la lista de las particiones del número n. Por ejemplo,

particiones 4  ==  [[4],[3,1],[2,2],[2,1,1],[1,1,1,1]]
particiones 5  ==  [[5],[4,1],[3,2],[3,1,1],[2,2,1],[2,1,1,1],[1,1,1,1,1]]
length (particiones 50)  ==  204226

Leer más…

El producto escalar de los vectores [a1,a2,...,an] y [b1,b2,..., bn] es

a1 * b1 + a2 * b2 + ··· + an * bn.

Definir la función

menorProductoEscalar :: (Ord a, Num a) => [a] -> [a] -> a

tal que (menorProductoEscalar xs ys) es el mínimo de los productos escalares de las permutaciones de xs y de las permutaciones de ys. Por ejemplo,

menorProductoEscalar [3,2,5]  [1,4,6]    == 29
menorProductoEscalar [3,2,5]  [1,4,-6]   == -19
menorProductoEscalar [1..10^2] [1..10^2] == 171700
menorProductoEscalar [1..10^3] [1..10^3] == 167167000
menorProductoEscalar [1..10^4] [1..10^4] == 166716670000
menorProductoEscalar [1..10^5] [1..10^5] == 166671666700000
menorProductoEscalar [1..10^6] [1..10^6] == 166667166667000000

Leer más…

Los puntos se puede representar mediante pares de números

type Punto = (Int,Int)

y las regiones rectangulares mediante el siguiente tipo de dato

data Region = Rectangulo Punto  Punto
| Union      Region Region
| Diferencia Region Region
deriving (Eq, Show)

donde

• (Rectangulo p1 p2) es la región formada por un rectángulo cuyo vértice superior izquierdo es p1 y su vértice inferior derecho es p2.
• (Union r1 r2) es la región cuyos puntos pertenecen a alguna de las regiones r1 y r2.
• (Diferencia r1 r2) es la región cuyos puntos pertenecen a la región r1 pero no pertenecen a la r2.

Definir la función

enRegion :: Punto -> Region -> Bool

tal que (enRegion p r) se verifica si el punto p pertenece a la región r. Por ejemplo, usando las regiones definidas por

r0021, r3051, r4162 :: Region
r0021 = Rectangulo (0,0) (2,1)
r3051 = Rectangulo (3,0) (5,1)
r4162 = Rectangulo (4,1) (6,2)

se tiene

enRegion (1,0) r0021                                   ==  True
enRegion (3,0) r0021                                   ==  False
enRegion (1,1) (Union r0021 r3051)                     ==  True
enRegion (4,0) (Union r0021 r3051)                     ==  True
enRegion (4,2) (Union r0021 r3051)                     ==  False
enRegion (3,1) (Diferencia r3051 r4162)                ==  True
enRegion (4,1) (Diferencia r3051 r4162)                ==  False
enRegion (4,2) (Diferencia r3051 r4162)                ==  False
enRegion (4,2) (Union (Diferencia r3051 r4162) r4162)  ==  True

Comprobar con QuickCheck que si el punto p está en la región r1, entonces, para cualquier región r2, p está en (Union r1 r2) y en (Union r2 r1), pero no está en (Diferencia r2 r1).

Leer más…

Un conjunto A está cerrado respecto de una función f si para elemento x de A se tiene que f(x) pertenece a A. La clausura de un conjunto B respecto de una función f es el menor conjunto A que contiene a B y es cerrado respecto de f. Por ejemplo, la clausura de {0,1,2] respecto del opuesto es {-2,-1,0,1,2}.

Definir la función

clausura :: Ord a => (a -> a) -> [a] -> [a]

tal que (clausura f xs) es la clausura de xs respecto de f. Por ejemplo,

clausura (\x -> -x) [0,1,2]         ==  [-2,-1,0,1,2]
clausura (\x -> (x+1) `mod` 5) [0]  ==  [0,1,2,3,4]
length (clausura (\x -> (x+1) `mod` (10^6)) [0]) == 1000000

Leer más…

Definir la lista

numerosConDigitosPrimos :: [Integer]

cuyos elementos son los números con todos sus dígitos primos. Por ejemplo,

λ> take 22 numerosConDigitosPrimos
[2,3,5,7,22,23,25,27,32,33,35,37,52,53,55,57,72,73,75,77,222,223]
λ> numerosConDigitosPrimos4 !! (10^7)
322732232572

Leer más…

Definir la función

producto :: [[a]] -> [[a]]

tal que (producto xss) es el producto cartesiano de los conjuntos xss. Por ejemplo,

λ> producto [[1,3],[2,5]]
[[1,2],[1,5],[3,2],[3,5]]
λ> producto [[1,3],[2,5],[6,4]]
[[1,2,6],[1,2,4],[1,5,6],[1,5,4],[3,2,6],[3,2,4],[3,5,6],[3,5,4]]
λ> producto [[1,3,5],[2,4]]
[[1,2],[1,4],[3,2],[3,4],[5,2],[5,4]]
λ> producto []
[[]]

Comprobar con QuickCheck que para toda lista de listas de números enteros, xss, se verifica que el número de elementos de (producto xss) es igual al producto de los números de elementos de cada una de las listas de xss.

Leer más…

Los primeros números de Fibonacci son

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

tales que los dos primeros son iguales a 1 y los siguientes se obtienen sumando los dos anteriores.

El teorema de Zeckendorf establece que todo entero positivo n se puede representar, de manera única, como la suma de números de Fibonacci no consecutivos decrecientes. Dicha suma se llama la representación de Zeckendorf de n. Por ejemplo, la representación de Zeckendorf de 100 es

100 = 89 + 8 + 3

Hay otras formas de representar 100 como sumas de números de Fibonacci; por ejemplo,

100 = 89 +  8 + 2 + 1
100 = 55 + 34 + 8 + 3

pero no son representaciones de Zeckendorf porque 1 y 2 son números de Fibonacci consecutivos, al igual que 34 y 55.

Definir la función

zeckendorf :: Integer -> [Integer]

tal que (zeckendorf n) es la representación de Zeckendorf de n. Por ejemplo,

zeckendorf 100 == [89,8,3]
zeckendorf 200 == [144,55,1]
zeckendorf 300 == [233,55,8,3,1]
length (zeckendorf (10^50000)) == 66097

Leer más…

Se dice que una sucesión x(1), ..., x(n) está ordenada cíclicamente si existe un índice i tal que la sucesión

x(i), x(i+1), ..., x(n), x(1), ..., x(i-1)

está ordenada crecientemente de forma estricta.

Definir la función

ordenadaCiclicamente :: Ord a => [a] -> Maybe Int

tal que (ordenadaCiclicamente xs) es el índice a partir del cual está ordenada, si la lista está ordenado cíclicamente y Nothing en caso contrario. Por ejemplo,

ordenadaCiclicamente [1,2,3,4]      ==  Just 0
ordenadaCiclicamente [5,8,1,3]      ==  Just 2
ordenadaCiclicamente [4,6,7,5,1,3]  ==  Nothing
ordenadaCiclicamente [1,0,3,2]      ==  Nothing
ordenadaCiclicamente [1,2,0]        ==  Just 2
ordenadaCiclicamente "cdeab"        ==  Just 3

Nota: Se supone que el argumento es una lista no vacía sin elementos repetidos.

Leer más…

Definir la función

eliminaAisladas :: Eq a => a -> [a] -> [a]

tal que (eliminaAisladas x ys) es la lista obtenida eliminando ys las ocurrencias aisladas de x (es decir, aquellas ocurrencias de x tales que su elemento anterior y posterior son distintos de x). Por ejemplo,

eliminaAisladas 'X' ""                  == ""
eliminaAisladas 'X' "X"                 == ""
eliminaAisladas 'X' "XX"                == "XX"
eliminaAisladas 'X' "XXX"               == "XXX"
eliminaAisladas 'X' "abcd"              == "abcd"
eliminaAisladas 'X' "Xabcd"             == "abcd"
eliminaAisladas 'X' "XXabcd"            == "XXabcd"
eliminaAisladas 'X' "XXXabcd"           == "XXXabcd"
eliminaAisladas 'X' "abcdX"             == "abcd"
eliminaAisladas 'X' "abcdXX"            == "abcdXX"
eliminaAisladas 'X' "abcdXXX"           == "abcdXXX"
eliminaAisladas 'X' "abXcd"             == "abcd"
eliminaAisladas 'X' "abXXcd"            == "abXXcd"
eliminaAisladas 'X' "abXXXcd"           == "abXXXcd"
eliminaAisladas 'X' "XabXcdX"           == "abcd"
eliminaAisladas 'X' "XXabXXcdXX"        == "XXabXXcdXX"
eliminaAisladas 'X' "XXXabXXXcdXXX"     == "XXXabXXXcdXXX"
eliminaAisladas 'X' "XabXXcdXeXXXfXx"   == "abXXcdeXXXfx"

Leer más…

Los árboles se pueden representar mediante el siguiente tipo de datos

data Arbol a = N a [Arbol a]
  deriving (Show, Eq)

Por ejemplo, los árboles

  1               3
 / \             /|\
6   3           / | \
    |          5  4  7
    5          |     /\
               6    2  1

se representan por

ej1, ej2 :: Arbol Int
ej1 = N 1 [N 6 [],N 3 [N 5 []]]
ej2 = N 3 [N 5 [N 6 []], N 4 [], N 7 [N 2 [], N 1 []]]

Definir la función

emparejaArboles :: (a -> b -> c) -> Arbol a -> Arbol b -> Arbol c

tal que (emparejaArboles f a1 a2) es el árbol obtenido aplicando la función f a los elementos de los árboles a1 y a2 que se encuentran en la misma posición. Por ejemplo,

λ> emparejaArboles (+) (N 1 [N 2 [], N 3[]]) (N 1 [N 6 []])
N 2 [N 8 []]
λ> emparejaArboles (+) ej1 ej2
N 4 [N 11 [],N 7 []]
λ> emparejaArboles (+) ej1 ej1
N 2 [N 12 [],N 6 [N 10 []]]

Leer más…

Definir la función

particion :: [a] -> ([a],[a])

tal que (particion xs) es el par cuya primera componente son los elementos de xs en posiciones pares y su segunda componente son los restantes elementos. Por ejemplo,

particion [3,5,6,2]    ==  ([3,6],[5,2])
particion [3,5,6,2,7]  ==  ([3,6,7],[5,2])
particion "particion"  ==  ("priin","atco")

Leer más…

Se dice que en una sucesión de números x(1), x(2), ..., x(n) hay una inversión cuando existe un par de números x(i) > x(j), siendo i < j. Por ejemplo, en la permutación 2, 1, 4, 3 hay dos inversiones (2 antes que 1 y 4 antes que 3) y en la permutación 4, 3, 1, 2 hay cinco inversiones (4 antes 3, 4 antes 1, 4 antes 2, 3 antes 1, 3 antes 2).

Definir la función

numeroInversiones :: Ord a => [a] -> Int

tal que (numeroInversiones xs) es el número de inversiones de xs. Por ejemplo,

numeroInversiones [2,1,4,3]  ==  2
numeroInversiones [4,3,1,2]  ==  5

Leer más…

Los números triangulares se forman como sigue

*     *      *
     * *    * *
           * * *
1     3      6

La sucesión de los números triangulares se obtiene sumando los números naturales. Así, los 5 primeros números triangulares son

 1 = 1
 3 = 1 + 2
 6 = 1 + 2 + 3
10 = 1 + 2 + 3 + 4
15 = 1 + 2 + 3 + 4 + 5

Definir la función

descomposicionesTriangulares :: Int -> [(Int, Int, Int)]

tal que (descomposicionesTriangulares n) es la lista de las ternas correspondientes a las descomposiciones de n en tres sumandos formados por números triangulares. Por ejemplo,

descomposicionesTriangulares  4 == []
descomposicionesTriangulares  5 == [(1,1,3)]
descomposicionesTriangulares 12 == [(1,1,10),(3,3,6)]
descomposicionesTriangulares 30 == [(1,1,28),(3,6,21),(10,10,10)]
descomposicionesTriangulares 61 == [(1,15,45),(3,3,55),(6,10,45),(10,15,36)]
descomposicionesTriangulares 52 == [(1,6,45),(1,15,36),(3,21,28),(6,10,36),(10,21,21)]
descomposicionesTriangulares 82 == [(1,3,78),(1,15,66),(1,36,45),(6,10,66),(6,21,55),(10,36,36)]

Leer más…

Definir la función

indicesVerdaderos :: [Int] -> [Bool]

tal que (indicesVerdaderos xs) es la lista infinita de booleanos tal que sólo son verdaderos los elementos cuyos índices pertenecen a la lista estrictamente creciente xs. Por ejemplo,

λ> take 6 (indicesVerdaderos [1,4])
[False,True,False,False,True,False]
λ> take 6 (indicesVerdaderos [0,2..])
[True,False,True,False,True,False]
λ> take 3 (indicesVerdaderos [])
[False,False,False]
λ> take 6 (indicesVerdaderos [1..])
[False,True,True,True,True,True]
λ> last (take (8*10^7) (indicesVerdaderos [0,5..]))
False

Leer más…

Para la determinación de las alergia se utiliza los siguientes códigos para los alérgenos:

Huevos ........   1
Cacahuetes ....   2
Mariscos ......   4
Fresas ........   8
Tomates .......  16
Chocolate .....  32
Polen .........  64
Gatos ......... 128

Así, si Juan es alérgico a los cacahuetes y al chocolate, su puntuación es 34 (es decir, 2+32).

Los alérgenos se representan mediante el siguiente tipo de dato

data Alergeno = Huevos
              | Cacahuetes
              | Mariscos
              | Fresas
              | Tomates
              | Chocolate
              | Polen
              | Gatos
  deriving (Enum, Eq, Show, Bounded)

Definir la función

alergias :: Int -> [Alergeno]

tal que (alergias n) es la lista de alergias correspondiente a una puntuación n. Por ejemplo,

λ> alergias 1
[Huevos]
λ> alergias 2
[Cacahuetes]
λ> alergias 3
[Huevos,Cacahuetes]
λ> alergias 5
[Huevos,Mariscos]
λ> alergias 255
[Huevos,Cacahuetes,Mariscos,Fresas,Tomates,Chocolate,Polen,Gatos]

Leer más…

Definir la función

reiteracion :: (a -> a) -> Int -> a -> a

tal que (reiteracion f n x) es el resultado de aplicar n veces la función f a x. Por ejemplo,

reiteracion (+1) 10 5  ==  15
reiteracion (+5) 10 0  ==  50
reiteracion (*2)  4 1  ==  16
reiteracion (5:)  4 [] ==  [5,5,5,5]

Leer más…

Las matrices pueden representarse mediante tablas cuyos índices son pares de números naturales. Su tipo se define por

type Matriz = Array (Int,Int) Int

Por ejemplo, la matriz

|9 4 6 5|
|8 1 7 3|
|4 2 5 4|

se define por

ej :: Matriz
ej = listArray ((1,1),(3,4)) [9,4,6,5,8,1,7,3,4,2,5,4]

Los vecinos de un elemento son los que están a un paso en la misma fila, columna o diagonal. Por ejemplo, en la matriz anterior, el 1 tiene 8 vecinos (el 9, 4, 6, 8, 7, 4, 2 y 5) pero el 9 sólo tiene 3 vecinos (el 4, 8 y 1).

Definir la función

algunoMenor :: Matriz -> [Int]

tal que (algunoMenor p) es la lista de los elementos de p que tienen algún vecino menor que él. Por ejemplo,

algunoMenor ej == [9,4,6,5,8,7,4,2,5,4]

pues sólo el 1 y el 3 no tienen ningún vecino menor en la matriz.

Leer más…

Los árboles binarios se pueden representar mediante el tipo Arbol definido por

data Arbol a = H a
             | N (Arbol a) a (Arbol a)
   deriving Show

Por ejemplo, el árbol

      "B"
      / \
     /   \
    /     \
  "B"     "A"
  / \     / \
"A" "B" "C" "C"

se puede definir por

ej1 :: Arbol String
ej1 = N (N (H "A") "B" (H "B")) "B" (N (H "C") "A" (H "C"))

Definir la función

enumeraArbol :: Arbol t -> Arbol Int

tal que (enumeraArbol a) es el árbol obtenido numerando las hojas y los nodos de a desde la hoja izquierda hasta la raíz. Por ejemplo,

λ> enumeraArbol ej1
N (N (H 0) 1 (H 2)) 3 (N (H 4) 5 (H 6))

Gráficamente,

      3
     / \
    /   \
   /     \
  1       5
 / \     / \
0   2   4   6

Leer más…

Los números triangulares se forman como sigue

*     *      *
     * *    * *
           * * *
1     3      6

La sucesión de los números triangulares se obtiene sumando los números naturales. Así, los 5 primeros números triangulares son

 1 = 1
 3 = 1 + 2
 6 = 1 + 2 + 3
10 = 1 + 2 + 3 + 4
15 = 1 + 2 + 3 + 4 + 5

Definir la función

triangularesConCifras :: Int -> [Integer]

tal que (triangulares n) es la lista de los números triangulares con n cifras distintas. Por ejemplo,

take 6 (triangularesConCifras 1)   ==  [1,3,6,55,66,666]
take 6 (triangularesConCifras 2)   ==  [10,15,21,28,36,45]
take 6 (triangularesConCifras 3)   ==  [105,120,136,153,190,210]
take 5 (triangularesConCifras 4)   ==  [1035,1275,1326,1378,1485]
take 2 (triangularesConCifras 10)  ==  [1062489753,1239845706]

Leer más…

Definir la función

trenza :: [a] -> [a] -> [a]

tal que (trenza xs ys) es la lista obtenida intercalando los elementos de xs e ys. Por ejemplo,

trenza [5,1] [2,7,4]             ==  [5,2,1,7]
trenza [5,1,7] [2..]             ==  [5,2,1,3,7,4]
trenza [2..] [5,1,7]             ==  [2,5,3,1,4,7]
take 8 (trenza [2,4..] [1,5..])  ==  [2,1,4,5,6,9,8,13]

Leer más…

Definir la función

biparticiones :: [a] -> [([a],[a])]

tal que (biparticiones xs) es la lista de pares formados por un prefijo de xs y el resto de xs. Por ejemplo,

λ> biparticiones [3,2,5]
[([],[3,2,5]),([3],[2,5]),([3,2],[5]),([3,2,5],[])]
λ> biparticiones "Roma"
[("","Roma"),("R","oma"),("Ro","ma"),("Rom","a"),("Roma","")]

Leer más…

Definir la función

listaCuadrada :: Int -> a -> [a] -> [[a]]

tal que (listaCuadrada n x xs) es una lista de n listas de longitud n formadas con los elementos de xs completada con x, si no xs no tiene suficientes elementos. Por ejemplo,

listaCuadrada 3 7 [0,3,5,2,4]  ==  [[0,3,5],[2,4,7],[7,7,7]]
listaCuadrada 3 7 [0..]        ==  [[0,1,2],[3,4,5],[6,7,8]]
listaCuadrada 2 'p' "eva"      ==  ["ev","ap"]
listaCuadrada 2 'p' ['a'..]    ==  ["ab","cd"]