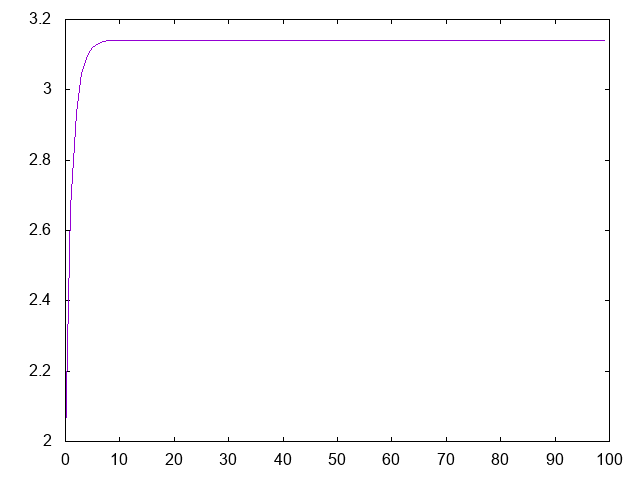
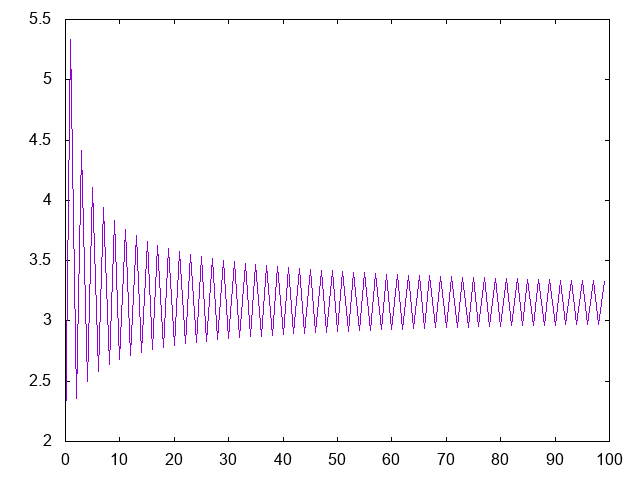
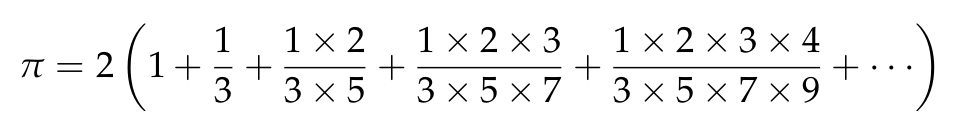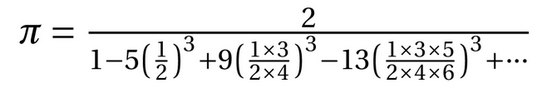Mayor órbita de la sucesión de Collatz
Se considera la siguiente operación, aplicable a cualquier número entero positivo:
- Si el número es par, se divide entre 2.
- Si el número es impar, se multiplica por 3 y se suma 1.
Dado un número cualquiera, podemos calcular su órbita; es decir, las imágenes sucesivas al iterar la función. Por ejemplo, la órbita de 13 es
13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1,...
Si observamos este ejemplo, la órbita de 13 es periódica, es decir, se repite indefinidamente a partir de un momento dado). La conjetura de Collatz dice que siempre alcanzaremos el 1 para cualquier número con el que comencemos. Ejemplos:
- Empezando en n = 6 se obtiene 6, 3, 10, 5, 16, 8, 4, 2, 1.
- Empezando en n = 11 se obtiene: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
- Empezando en n = 27, la sucesión tiene 112 pasos, llegando hasta 9232 antes de descender a 1: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1.
Definir la función
mayoresGeneradores :: Integer -> [Integer]
tal que (mayoresGeneradores n) es la lista de los números menores o iguales que n cuyas órbitas de Collatz son las de mayor longitud. Por ejemplo,
mayoresGeneradores 20 == [18,19] mayoresGeneradores (10^6) == [837799]