Definir las funciones

multiplosDeLaLongitud :: [Int] -> [Int]
multiplosDeLaLongitudDeConsecutivos :: Int -> Int -> [Int]

tales que

• (multiplosDeLaLongitud xs) es la lista de los elementos de xs que son múltiplos de la longitud de xs. Por ejemplo,

multiplosDeLaLongitud [2,4,6,8] == [4,8]

• (multiplosDeLaLongitudDeConsecutivos n m) es la lista de elementos de [n..n+m-1] que son múltiplos de n. Por ejemplo,

multiplosDeLaLongitudDeConsecutivos 9 2  ==  [10]
multiplosDeLaLongitudDeConsecutivos 9 12 ==  [12]

Comprobar con QuickCheck si se verifican las siguientes propiedades

• En cualquier conjunto de m elementos consecutivos, m divide exactamente a uno de dichos elementos. En otras palabras, si n y m son enteros positivos, entonces (multiplosDeLaLongitudDeConsecutivos n m) tiene exactamente un elemento.
• Si n es un entero positivo y m >= n, entonces (multiplosDeLaLongitudDeConsecutivos n m) es igual a [m]
• Si n y n son enteros positivos y m < n, entonces (multiplosDeLaLongitudDeConsecutivos n m) es igual a [m * ceiling (n' / m')] donde n' y m' son las formas decimales de n y m respectivamente.

Leer más…

La conjetura de Catalan, enunciada en 1844 por Eugène Charles Catalan y demostrada 2002 por Preda Mihăilescu1, afirma que

Las únicas dos potencias de números enteros consecutivos son 8 y 9 (que son respectivamente 2³ y 3²).

En otras palabras, la única solución entera de la ecuación

x^a - y^b = 1

para x, a, y, b > 1 es x = 3, a = 2, y = 2, b = 3.

La conjetura de Pillai, propuesta por S.S. Pillai en 1942, generaliza este resultado y es un problema abierto. Afirma que cada entero se puede escribir sólo un número finito de veces como una diferencia de dos potencias perfectas. En otras palabras, para todo entero positivo n, el conjunto de soluciones de

x^a - y^b = n

para x, a, y, b > 1 es finito.

Por ejemplo, para n = 4, hay 3 soluciones

(2,3, 2,2) ya que 2³ -  2² =   8 -   4 = 4
(6,2, 2,5) ya que 6² -  2⁵ =  36 -  32 = 4
(5,3,11,2) ya que 5³ - 11² = 125 - 121 = 4

Las soluciones se pueden representar por la menor potencia (en el caso anterior, por 4, 32 y 121) ya que dado n (en el caso anterior es 4), la potencia mayor es la menor más n.

Definir las funciones

potenciasPerfectas :: [Integer]
solucionesPillati :: Integer -> [Integer]
solucionesPillatiAcotadas :: Integer -> Integer -> [Integer]

tales que

• potenciasPerfectas es la lista de las potencias perfectas (es decir, de los números de la forma x^a con x y a mayores que 1). Por ejemplo,

take 10 potenciasPerfectas  ==  [4,8,9,16,25,27,32,36,49,64]
potenciasPerfectas !! 200   ==  28224

• (solucionesPillati n) es la lista de las menores potencias de las soluciones de la ecuación de Pillati x^a - y^b = n; es decir, es la lista de los u tales que u y u+n son potencias perfectas. Por ejemplo,

take 3 (solucionesPillati 4)  ==  [4,32,121]
take 2 (solucionesPillati 5)  ==  [4,27]
take 4 (solucionesPillati 7)  ==  [9,25,121,32761]

• (solucionesPillatiAcotadas c n) es la lista de elementos de (solucionesPillati n) menores que n. Por ejemplo,

solucionesPillatiAcotadas (10^3) 1  ==  [8]
solucionesPillatiAcotadas (10^3) 2  ==  [25]
solucionesPillatiAcotadas (10^3) 3  ==  [125]
solucionesPillatiAcotadas (10^3) 4  ==  [4,32,121]
solucionesPillatiAcotadas (10^3) 5  ==  [4,27]
solucionesPillatiAcotadas (10^3) 6  ==  []
solucionesPillatiAcotadas (10^3) 7  ==  [9,25,121]
solucionesPillatiAcotadas (10^5) 7  ==  [9,25,121,32761]

Leer más…

La 40ª Conferencia General de la UNESCO ha proclamado el de enero el Día mundial de la Lógica. La fecha del 14 de enero se ha eligido para rendir homenaje a dos grandes lógicos del siglo XX: Kurt Gödel (que falleció el 14 de enero de 1978) y Alfred Tarski (que nació el 14 de enero de 1901).

Gödel demostró en 1931 los teoremas de incompletitud y para su demostración introdujo la actualmente conocida como codificación de Gödel que asigna a cada fórmula de un lenguaje formal un número único.

En este ejercicio aplicaremos la codificación de Gödel a las listas de números enteros.

Dada una lista de números naturales xs, la codificación de Gödel de xs se obtiene multiplicando las potencias de los primos sucesivos, siendo los exponentes los sucesores de los elementos de xs. Por ejemplo, si xs es [6,0,4], la codificación de xs es

2^(6+1) * 3^(0+1) * 5^(4+1) = 1200000

Definir las funciones

codificaG   :: [Integer] -> Integer
decodificaG :: Integer -> [Integer]

tales que

• (codificaG xs) es la codificación de Gödel de xs. Por ejemplo,

codificaG [6,0,4]            ==  1200000
codificaG [3,1,1]            ==  3600
codificaG [3,1,0,0,0,0,0,1]  ==  4423058640
codificaG [1..6]             ==  126111168580452537982500

• (decodificaG n) es la lista xs cuya codificación es n. Por ejemplo,

decodificaG 1200000                   ==  [6,0,4]
decodificaG 3600                      ==  [3,1,1]
decodificaG 4423058640                ==  [3,1,0,0,0,0,0,1]
decodificaG 126111168580452537982500  ==  [1,2,3,4,5,6]

Comprobar con QuickCheck que decodificaG es la inversa por la izquierda de codificaG; es decir, para toda lista xs de números enteros, se verifica que

decodificaG (codificaG ys) == ys

donde ys es la lista de los valores absolutos de los elementos de xs.

Leer más…

Un número de Munchausen es un número entero positivo tal que es igual a la suma de sus dígitos elevados a sí mismo. Por ejemplo, 3435 es un número de Munchausen ya que

3³ + 4⁴ + 3³ + 5⁵ = 27 + 256 + 27 + 3125 = 3435

Definir la función

esMunchausen :: Integer -> Bool

tal que (esMunchausen n) se verifica si n es un número de Munchausen. Por ejemplo,

esMunchausen 3435  ==  True
esMunchausen 2020  ==  False

Comprobar con QuickCheck que que los únicos números de Munchausen son 1 y 3435.

Nota 1: No usar la propiedad en la definición.

Nota 2: El ejercicio está basado en el artículo ¿Por qué 3435 es uno de mis números favoritos? de Miguel Ángel Morales en El Aleph.

Leer más…

El teorema de existencia de divisores afirma que

En cualquier subconjunto de {1, 2, ..., 2m} con al menos m+1 elementos existen números distintos a, b tales que a divide a b.

Un conjunto de números naturales xs es mayoritario si existe un m tal que la lista de xs es un subconjunto de {1,2,...,2m} con al menos m+1 elementos. Por ejemplo, {2,3,5,6} porque es un subconjunto de {1,2,...,6} con más de 3 elementos.

Definir las funciones

divisoresMultiplos :: [Integer] -> [(Integer,Integer)]
esMayoritario :: [Integer] -> Bool

tales que

• (divisores xs) es la lista de pares de elementos distintos de (a,b) tales que a divide a b. Por ejemplo,

divisoresMultiplos [2,3,5,6]  ==  [(2,6),(3,6)]
divisoresMultiplos [2,3,5]    ==  []
divisoresMultiplos [4..8]     ==  [(4,8)]

• (esMayoritario xs) se verifica xs es mayoritario. Por ejemplo,

esMayoritario [2,3,5,6]  ==  True
esMayoritario [2,3,5]    ==  False

Comprobar con QuickCheck el teorema de existencia de divisores; es decir, en cualquier conjunto mayoritario existen números distintos a, b tales que a divide a b. Para la comprobación se puede usar el siguiente generador de conjuntos mayoritarios

mayoritario :: Gen [Integer]
mayoritario = do
  m' <- arbitrary
  let m = 1 + abs m'
  xs' <- sublistOf [1..2*m] `suchThat` (\ys -> genericLength ys > m)
  return xs'

con lo que la propiedad que hay que comprobar con QuickCheck es

teorema_de_existencia_de_divisores :: Property
teorema_de_existencia_de_divisores =
  forAll mayoritario (not . null . divisoresMultiplos)

Leer más…

El problema de Waring, propuesto por Edward Waring consiste en determinar si, para cada número entero k mayor que 1, existe un número n tal que todo entero positivo se puede escribir como una suma de k-potencias de números positivos con n sumandos como máximo.

La respuesta afirmativa al problema, aportada por David Hilbert, se conoce como el teorema de Hilbert-Waring. Su enunciado es

Para cada número entero k, con k ≥ 2, existe un entero positivo g(k) tal que todo entero positivo se puede expresar como una suma de a lo más g(k) k-ésimas potencias.

Definir las funciones

descomposiciones :: Integer -> Integer -> Integer -> [[Integer]]
orden :: Integer -> Integer -> Integer

tales que

• (descomposiciones x k n) es la lista de descomposiciones de x como suma de n potencias con exponente k de números enteros positivos.

descomposiciones 9   2 1  ==  [[9]]
descomposiciones 9   3 1  ==  []
descomposiciones 9   3 2  ==  [[1,8]]
descomposiciones 9   4 9  ==  [[1,1,1,1,1,1,1,1,1]]
descomposiciones 25  2 2  ==  [[9,16]]
descomposiciones 133 2 3  ==  [[8,125]]
descomposiciones 38  3 2  ==  [[1,1,36],[4,9,25]]

• (orden x k) es el menor número de sumandos necesario para expresar x como suma de k-ésimas potencias. Por ejemplo,

orden 9  2  ==  1
orden 9  3  ==  2
orden 9  4  ==  9
orden 10 2  ==  2
orden 10 3  ==  3
orden 10 4  ==  10
[maximum [orden x k | x <- [1..1000]] | k <- [1..6]] == [1,4,9,19,37,73]

Comprobar el teorema de Hilbert-Waring para k hasta 7; es decir, para todo número x positivo se verifica que

orden x 2 <= 4
orden x 3 <= 9
orden x 4 <= 19
orden x 5 <= 37
orden x 6 <= 73
orden x 7 <= 143

y, en general,

orden x k <= 2^k + floor ((3/2)^k) - 2

Leer más…

Dos números enteros son coprimos (o primos entre sí) si no tienen ningún factor primo en común. Por ejemplo, 4 y 15 son coprimos.

Una terna coprima es una terna (a,b,c) tal que

• a y b son coprimos,
• a y c son coprimos y
• b y c son coprimos.

Por ejemplo, (3,4,5) es una terna coprima.

Definir la función

sumas3coprimos :: Integer -> [(Integer,Integer,Integer)]

tal que (sumas3coprimos n) es la lista de las ternas coprimas cuya suma es n. Por ejemplo,

sumas3coprimos 10  ==  [(2,3,5)]
sumas3coprimos 11  ==  []
sumas3coprimos 12  ==  [(2,3,7),(3,4,5)]
length (sumas3coprimos 4000)  ==  546146

Comprobar con QuickCheck que todo número entero mayor que 15 se puede escribir como suma de alguna terna coprima; es decir, para todo entero n, (sumas3coprimos2 (18 + abs n)) tiene algún elemento.

Leer más…

Para cada número entero positivo n, se define el conjunto

S(n) = {1, 2, 3, ..., n}

de los números desde el 1 hasta n.

Definir la función

mayorPotenciaDeDosEnS :: Integer -> Integer

tal que (mayorPotenciaDeDosEnS n) es la mayor potencia de 2 en S(n). Por ejemplo,

mayorPotenciaDeDosEnS 3  ==  2
mayorPotenciaDeDosEnS 4  ==  4

Comprobar con QuickCheck que la mayor potencia de 2 en S(n) no divide a ningún otro elemento de S(n).

Leer más…

Sea S el conjunto

S = {1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, ...}

de los enteros positivos congruentes con 1 módulo 4; es decir,

S = {4n+1 | n ∈ N}

Un elemento n de S es irreducible si sólo es divisible por dos elementos de S: 1 y n. Por ejemplo, 9 es irreducible; pero 45 no lo es (ya que es el proctos de 5 y 9 que son elementos de S).

Definir las funciones

esIrreducible :: Integer -> Bool
factorizaciones :: Integer -> [[Integer]]
conFactorizacionNoUnica :: [Integer]

tales que

• (esIrreducible n) se verifica si n es irreducible. Por ejemplo,

esIrreducible 9   ==  True
esIrreducible 45  ==  False

• (factorizaciones n) es la lista de conjuntos de elementos irreducibles de S cuyo producto es n. Por ejemplo,

factorizaciones 9     ==  [[9]]
factorizaciones 693   ==  [[9,77],[21,33]]
factorizaciones 4389  ==  [[21,209],[33,133],[57,77]]

• conFactorizacionNoUnica es la lista de elementos de S cuya factorización no es única. Por ejemplo,

λ> take 10 conFactorizacionNoUnica
[441,693,1089,1197,1449,1617,1881,1953,2205,2277]

Leer más…

Una lista CuCu es una lista de números enteros positivos tales que la suma de sus Cubos es igual al Cuadrado de su suma. Por ejemplo, [1, 2, 3, 2, 4, 6] es una lista CuCu ya que

1³ + 2³ + 3³ + 2³ + 4³ + 6³ = (1 + 2 + 3 + 2 + 4 + 6)²

La lista de Liouville correspondiente al número entero positivo n es la lista formada por el número de divisores de cada divisor de n. Por ejemplo, para el número 20 se tiene que sus divisores son

1, 2, 4, 5, 10, 20

puesto que el número de sus divisores es

• El 1 tiene 1 divisor (el 1 solamente).
• El 2 tiene 2 divisores (el 1 y el 2).
• El 4 tiene 3 divisores (el 1, el 2 y el 4).
• El 5 tiene 2 divisores (el 1 y el 5).
• El 10 tiene 4 divisores (el 1, el 2, el 5 y el 10).
• El 20 tiene 6 divisores (el 1, el 2, el 4, el 5, el 10 y el 20).

la lista de Liouville de 20 es [1, 2, 3, 2, 4, 6] que, como se comentó anteriormente, es una lista CuCu.

El teorema de Lioville afirma que todas las lista de Lioville son CuCu.

Definir las funciones

esCuCu :: [Integer] -> Bool
liouville :: Integer -> [Integer]

tales que

• (esCuCu xs) se verifica si la lista xs es CuCu; es decir, la suma de los cubos de sus elementos es igual al cuadrado de su suma. Por ejemplo,

esCuCu [1,2,3]        ==  True
esCuCu [1,2,3,2]      ==  False
esCuCu [1,2,3,2,4,6]  ==  True

• (liouville n) es la lista de Lioville correspondiente al número n. Por ejemplo,

liouville 20  ==  [1,2,3,2,4,6]
liouville 60  ==  [1,2,2,3,2,4,4,6,4,6,8,12]
length (liouville (product [1..25]))  ==  340032

Comprobar con QuickCheck

• que para todo entero positivo n, (liouville (2^n)) es la lista [1,2,3,...,n+1] y
• el teorema de Lioville; es decir, para todo entero positivo n, (liouville n) es una lista CuCu.

Nota: Este ejercicio está basado en Cómo generar conjuntos CuCu de Gaussianos.

Leer más…

La conjetura de Grimm establece que a cada elemento de un conjunto de números compuestos se puede asignar número primo que lo divide, de forma que cada uno de los números primos elegidos es distinto de todos los demás. Más formalmente, si n+1, n+2, ..., n+k son números compuestos, entonces existen números primos p(i), distintos entre sí, tales que p(i) divide a n+i para 1 ≤ i ≤ k.

Diremos que la lista ps = [p(1),...,p(k)] es una sucesión de Grim para la lista xs = [x(1),...,x(k)] si p(i) son números primos distintos y p(i) divide a x(i), para 1 ≤ i ≤ k. Por ejemplo, 2, 5, 13, 3, 7 es una sucesión de Grim de 24, 25, 26, 27, 28.

Definir las funciones

compuestos :: Integer -> [Integer]
sucesionesDeGrim :: [Integer] -> [[Integer]]

tales que

• (compuestos n) es la mayor lista de números enteros consecutivos empezando en n. Por ejemplo,

compuestos 24  ==  [24,25,26,27,28]
compuestos  8  ==  [8,9,10]
compuestos 15  ==  [15,16]
compuestos 16  ==  [16]
compuestos 17  ==  []

• (sucesionesDeGrim xs) es la lista de las sucesiones de Grim de xs. Por ejemplo,

sucesionesDeGrim [15,16]          == [[3,2],[5,2]]
sucesionesDeGrim [8,9,10]         == [[2,3,5]]
sucesionesDeGrim [9,10]           == [[3,2],[3,5]]
sucesionesDeGrim [24,25,26,27,28] == [[2,5,13,3,7]]
sucesionesDeGrim [25,26,27,28]    == [[5,2,3,7],[5,13,3,2],[5,13,3,7]]

Comprobar con QuickCheck la conjetura de Grim; es decir, para todo número n > 1, (sucesionesDeGrim (compuestos n)) es una lista no vacía.

Leer más…

La sucesión de Fibonacci, F(n), es la siguiente sucesión infinita de números naturales:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...

La sucesión comieanza con los números 0 y 1. A partir de estos, cada término es la suma de los dos anteriores.

El teorema de Carmichael establece que para todo n mayor que 12, el n-ésimo número de Fibonacci F(n) tiene al menos un factor primo que no es factor de ninguno de los términos anteriores de la sucesión.

Si un número primo p es un factor de F(n) y no es factor de ningún F(m) con m < n, entonces se dice que p es un factor característico o un divisor primitivo de F(n).

Definir la función

factoresCaracteristicos :: Int -> [Integer]

tal que (factoresCaracteristicos n) es la lista de los factores característicos de F(n). Por ejemplo,

factoresCaracteristicos  4  ==  [3]
factoresCaracteristicos  6  ==  []
factoresCaracteristicos 19  ==  [37,113]
factoresCaracteristicos 37  ==  [73,149,2221]

Comprobar con QuickCheck el teorema de Carmichael; es decir, para todo número entero (factoresCaracteristicos (13 + abs n)) es una lista no vacía.

Leer más…

La derivada aritmética es una función definida sobre los números naturales por analogía con la regla del producto para el cálculo de las derivadas usada en análisis.

Para un número natural n su derivada D(n) se define por

D(0)  = 0
D(1)  = 0
D(p)  = 1, si p es primo
D(ab) = D(a)b + aD(b) (regla de Leibniz para derivar productos)

Por ejemplo,

D(6)  = D(2*3) = D(2)*3 + 2*D(3) = 1*3 + 2*1 =  5
D(12) = D(2*6) = D(2)*6 + 2*D(6) = 1*6 + 2*5 = 16

Definir la función

derivada :: Integer -> Integer

tal que (derivada n) es la derivada aritmérica de n. Por ejemplo,

derivada  6  ==  5
derivada 12  ==  16
maximum [derivada n | n <- [1..60000]]  ==  380928

Comprobar con QuickCheck que si x es un número entero positivo y su descomposición en factores primos es

x = p(1)^e(1) + p(2)^e(2) +...+ p(n)^e(n)

entonces la derivada de x es

x * [e(1)/p(1) + e(2)/p(2) +...+ e(n)/p(n)]

Nota: No usar en la definición la propiedad que hay que comprobar.

Leer más…

El postulado de Bertrand afirma que para cualquier número entero n > 1, existe al menos un número primo p con n < p < 2n.

Definir la función

siguientePrimo :: Integer -> Integer

tal que (siguientePrimo n) es el menor primo mayor que n. Por ejemplo,

siguientePrimo 8   ==  11
siguientePrimo 11  ==  13

Comprobar con QuickCheck el postulado de Bertrand; es decir, para todo entero n > 1, se verifica que n < p < 2n, donde p es (siguientePrimo n).

Leer más…

En un ejercicio anterior se mostró que los conjuntos finitos de números naturales se pueden enumerar como sigue

 0: []
 1: [0]
 2: [1]
 3: [1,0]
 4: [2]
 5: [2,0]
 6: [2,1]
 7: [2,1,0]
 8: [3]
 9: [3,0]
10: [3,1]
11: [3,1,0]
12: [3,2]
13: [3,2,0]
14: [3,2,1]
15: [3,2,1,0]
16: [4]
17: [4,0]
18: [4,1]
19: [4,1,0]

en la que los elementos están ordenados de manera decreciente.

Además, se definió la constante

enumeracionCFN :: [[Integer]]

tal que sus elementos son los conjuntos de los números naturales con la ordenación descrita anteriormente. Por ejemplo,

λ> take 20 enumeracionCFN
[[],
 [0],
 [1],[1,0],
 [2],[2,0],[2,1],[2,1,0],
 [3],[3,0],[3,1],[3,1,0],[3,2],[3,2,0],[3,2,1],[3,2,1,0],
 [4],[4,0],[4,1],[4,1,0]]

Definir la función

posicion :: [Integer] -> Integer

tal que (posicion xs) es la posición del conjunto finito de números naturales xs, representado por una lista decreciente, en enumeracionCFN. Por ejemplo,

posicion [2,0]          ==  5
posicion [2,1]          ==  6
posicion [2,1,0]        ==  7
posicion [0]            ==  1
posicion [1,0]          ==  3
posicion [2,1,0]        ==  7
posicion [3,2,1,0]      ==  15
posicion [4,3,2,1,0]    ==  31
posicion [5,4,3,2,1,0]  ==  63

Comprobar con QuickCheck que para todo número natural n,

posicion [n,n-1..0] == 2^(n+1) - 1.

Leer más…

Dado un conjunto de números naturales, por ejemplo A = {0, 2, 3, 4}, calculamos las sumas de todos los pares de elementos de A. Como A tiene 4 elementos hay 16 pares, pero no todas sus sumas son distintas. En este caso solo hay 8 sumas distintas: {0, 2, 3, 4, 5, 6, 7, 8}. Procediendo análogamente hay 9 diferencias distinatas entre los pares de A: {-4, -3, -2, -1, 0, 1, 2, 3, 4}.

Experimentando con más conjuntos, se puede conjeturar que el número de restas es mayor que el de sumas y argumentar que que mientras que con dos números distintos sólo se produce una suma distints sin embargo se producen dos restas distintas. Por ejemplo, con 5 y 7 sólo se produce una suma (ya que 5+7 y 7+5 ambos dan 12) pero dos restas (ya que 5-7 y 7-5 dan -2 y 2, respectivamente).

Sin embargo, la conjetura es falsa. Un contraejemplo en el conjunto {0, 2, 3, 4, 7, 11, 12, 14}, que tiene 26 sumas distintas con sus pares de elementos pero sólo 25 restas.

Los conjuntos con más sumas distintas con sus pares de elementos que restas se llaman conjuntos MSQR (por "más sumas que restas").

El objetivo de este ejercicio es calcular los conjuntos MSQR.

Definir las funciones

tieneMSQR :: [Integer] -> Bool
conjuntosMSQR :: [[Integer]]

tales que

• (tieneMSQR xs) se verifica si el conjunto xs tiene más sumas que restas. Por ejemplo,

tieneMSQR [0, 2, 3, 4]                 ==  False
tieneMSQR [0, 2, 3, 4, 7, 11, 12, 14]  ==  True

• conjuntosMSQR es la lista de los conjuntos MSQR. Por ejemplo,

λ> take 5 conjuntosMSQR
[[14,12,11,7,4,3,2,0],
 [14,12,11,10,7,3,2,0],
 [14,13,12,9,5,4,2,1,0],
 [14,13,12,10,9,5,2,1,0],
 [15,13,12,8,5,4,3,1]]

 length (takeWhile (< [14]) conjuntosMSQR)   ==  0
 length (takeWhile (< [15]) conjuntosMSQR)   ==  4
 length (takeWhile (< [16]) conjuntosMSQR)   ==  10
 length (takeWhile (< [17]) conjuntosMSQR)   ==  30

Leer más…

Los conjuntos finitos de números naturales se pueden enumerar como sigue

 0: []
 1: [0]
 2: [1]
 3: [1,0]
 4: [2]
 5: [2,0]
 6: [2,1]
 7: [2,1,0]
 8: [3]
 9: [3,0]
10: [3,1]
11: [3,1,0]
12: [3,2]
13: [3,2,0]
14: [3,2,1]
15: [3,2,1,0]
16: [4]
17: [4,0]
18: [4,1]
19: [4,1,0]

en la que los elementos están ordenados de manera decreciente.

Definir la constante

enumeracionCFN :: [[Integer]]

tal que sus elementos son los conjuntos de los números naturales con la ordenación descrita anteriormente. Por ejemplo,

λ> take 20 enumeracionCFN
[[],
 [0],
 [1],[1,0],
 [2],[2,0],[2,1],[2,1,0],
 [3],[3,0],[3,1],[3,1,0],[3,2],[3,2,0],[3,2,1],[3,2,1,0],
 [4],[4,0],[4,1],[4,1,0]]

Comprobar con QuickCheck que

• si (xs,ys) es un par de elementos consecutivos de enumeracionCFN, entonces xs < ys;
• todo conjunto finito de números naturales, representado por una lista decreciente, está en enumeracionCFN.

Leer más…

Un par de números primos (p,q) es un par de números primos gemelos si su distancia de 2; es decir, si q = p+2. Por ejemplo, (17,19) es una par de números primos gemelos.

La conjetura de los primos gemelos postula la existencia de infinitos pares de primos gemelos.

Definir la constante

primosGemelos :: [(Integer,Integer)]

tal que sus elementos son los pares de primos gemelos. Por ejemplo,

λ> take 7 primosGemelos
[(3,5),(5,7),(11,13),(17,19),(29,31),(41,43),(59,61)]
λ> primosGemelos !! (4*10^4)
(6381911,6381913)

Comprobar con QuickCheck la conjetura de los primos gemelos.

Leer más…

La sucesión de Fibonacci, F(n), es la siguiente sucesión infinita de números naturales:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...

La sucesión comienza con los números 0 y 1. A partir de estos, cada término es la suma de los dos anteriores.

Definir la función

sumaFibsIndiceImpar :: Int -> Integer

tal que (sumaFibsIndiceImpar n) es la suma de los n primeros términos de la sucesión de Fibonacci no índice impar; es decir,

sumaFibsIndiceImpar n = F(1) + F(3) + ... + F(2*n-1)

Por ejemplo,

sumaFibsIndiceImpar 1  ==  1
sumaFibsIndiceImpar 2  ==  3
sumaFibsIndiceImpar 3  ==  8
sumaFibsIndiceImpar 4  ==  21
sumaFibsIndiceImpar 5  ==  55
sumaFibsIndiceImpar (10^4) `rem` (10^9)  ==  213093125

En los ejemplos anteriores se observa que

sumaFibsIndiceImpar 1  ==  F(2)
sumaFibsIndiceImpar 2  ==  F(4)
sumaFibsIndiceImpar 3  ==  F(6)
sumaFibsIndiceImpar 4  ==  F(8)
sumaFibsIndiceImpar 5  ==  F(10)

Comprobar con QuickCheck que (sumaFibsIndiceImpar n) es F(2n); es decir, el 2n-ésimo número de Fibonacci

Leer más…

El 25 de diciembre de 1640, en una carta a Mersenne, Fermat demostró la conjetura de Girard: todo primo de la forma 4n+1 puede expresarse de manera única como suma de dos cuadrados. Por eso es conocido como el Teorema de Navidad de Fermat.

Definir las funciones

representaciones :: Integer -> [(Integer,Integer)]
primosImparesConRepresentacionUnica :: [Integer]
primos4nM1 :: [Integer]

tales que

• (representaciones n) es la lista de pares de números naturales (x,y) tales que n = x^2 + y^2 con x <= y. Por ejemplo,

representaciones  20           ==  [(2,4)]
representaciones  25           ==  [(0,5),(3,4)]
representaciones 325           ==  [(1,18),(6,17),(10,15)]
representaciones 100000147984  ==  [(0,316228)]
length (representaciones (10^10))    ==  6
length (representaciones (4*10^12))  ==  7

• primosImparesConRepresentacionUnica es la lista de los números primos impares que se pueden escribir exactamente de una manera como suma de cuadrados de pares de números naturales (x,y) con x <= y. Por ejemplo,

λ> take 20 primosImparesConRepresentacionUnica
[5,13,17,29,37,41,53,61,73,89,97,101,109,113,137,149,157,173,181,193]

• primos4nM1 es la lista de los números primos que se pueden escribir como uno más un múltiplo de 4 (es decir, que son congruentes con 1 módulo 4). Por ejemplo,

λ> take 20 primos4nM1
[5,13,17,29,37,41,53,61,73,89,97,101,109,113,137,149,157,173,181,193]

El teorema de Navidad de Fermat afirma que un número primo impar p se puede escribir exactamente de una manera como suma de dos cuadrados de números naturales p = x² + y^2 (con x <= y) si, y sólo si, p se puede escribir como uno más un múltiplo de 4 (es decir, que es congruente con 1 módulo 4).

Comprobar con QuickCheck el teorema de Navidad de Fermat; es decir, que para todo número n, los n-ésimos elementos de primosImparesConRepresentacionUnica y de primos4nM1 son iguales.

Leer más…

Las primeras sumas alternas de los factoriales son números primos; en efecto,

3! - 2! + 1! = 5
4! - 3! + 2! - 1! = 19
5! - 4! + 3! - 2! + 1! = 101
6! - 5! + 4! - 3! + 2! - 1! = 619
7! - 6! + 5! - 4! + 3! - 2! + 1! = 4421
8! - 7! + 6! - 5! + 4! - 3! + 2! - 1! = 35899

son primos, pero

9! - 8! + 7! - 6! + 5! - 4! + 3! - 2! + 1! = 326981

no es primo.

Definir las funciones

sumaAlterna         :: Integer -> Integer
sumasAlternas       :: [Integer]
conSumaAlternaPrima :: [Integer]

tales que

• (sumaAlterna n) es la suma alterna de los factoriales desde n hasta 1. Por ejemplo,

sumaAlterna 3  ==  5
sumaAlterna 4  ==  19
sumaAlterna 5  ==  101
sumaAlterna 6  ==  619
sumaAlterna 7  ==  4421
sumaAlterna 8  ==  35899
sumaAlterna 9  ==  326981

• sumasAlternas es la sucesión de las sumas alternas de factoriales. Por ejemplo,

λ> take 10 sumasAlternas
[0,1,1,5,19,101,619,4421,35899,326981]

• conSumaAlternaPrima es la sucesión de los números cuya suma alterna de factoriales es prima. Por ejemplo,

λ> take 8 conSumaAlternaPrima
[3,4,5,6,7,8,10,15]

Leer más…

El árbol binario de los divisores de 24 es

 90
 /\
2  45
   /\
  3  15
     /\
    3  5

Se puede representar por

N 90 (H 2) (N 45 (H 3) (N 15 (H 3) (H 5)))

usando el tipo de dato definido por

data Arbol = H Int
           | N Int Arbol Arbol
  deriving (Eq, Show)

Análogamente se obtiene el árbol binario de cualquier número x: se comienza en x y en cada paso se tiene dos hijos (su menor divisor y su cociente) hasta obtener números primos en las hojas.

Definir las funciones

arbolDivisores      :: Int -> Arbol
hojasArbolDivisores :: Int -> [Int]

tales que

• (arbolDivisores x) es el árbol binario de los divisores de x. Por ejemplo,

λ> arbolDivisores 90
N 90 (H 2) (N 45 (H 3) (N 15 (H 3) (H 5)))
λ> arbolDivisores 24
N 24 (H 2) (N 12 (H 2) (N 6 (H 2) (H 3)))
λ> arbolDivisores 300
N 300 (H 2) (N 150 (H 2) (N 75 (H 3) (N 25 (H 5) (H 5))))

• (hojasArbolDivisores x) es la lista de las hohas del árbol binario de los divisores de x. Por ejemplo

hojasArbolDivisores 90   ==  [2,3,3,5]
hojasArbolDivisores 24   ==  [2,2,2,3]
hojasArbolDivisores 300  ==  [2,2,3,5,5]

Leer más…

Definir la función

interseccion :: Ord a => [[a]] -> [a]

tal que (interseccion xss) es la intersección de la lista no vacía de listas infinitas crecientes xss; es decir, la lista de los elementos que pertenecen a todas las listas de xss. Por ejemplo,

λ> take 10 (interseccion [[2,4..],[3,6..],[5,10..]])
[30,60,90,120,150,180,210,240,270,300]
λ> take 10 (interseccion [[2,5..],[3,5..],[5,7..]])
[5,11,17,23,29,35,41,47,53,59]

Leer más…

La fórmula de Vieta para el cálculo de pi es la siguiente

Definir las funciones

aproximacionPi :: Int -> Double
errorPi :: Double -> Int

tales que

• (aproximacionPi n) es la aproximación de pi usando n factores de la fórmula de Vieta. Por ejemplo,

aproximacionPi  5  ==  3.140331156954753
aproximacionPi 10  ==  3.1415914215112
aproximacionPi 15  ==  3.141592652386592
aproximacionPi 20  ==  3.1415926535886207
aproximacionPi 25  ==  3.141592653589795

• (errorPi x) es el menor número de factores de la fórmula de Vieta necesarios para obtener pi con un error menor que x. Por ejemplo,

errorPi 0.1        ==  2
errorPi 0.01       ==  4
errorPi 0.001      ==  6
errorPi 0.0001     ==  7
errorPi 1e-4       ==  7
errorPi 1e-14      ==  24
pi                 ==  3.141592653589793
aproximacionPi 24  ==  3.1415926535897913

Leer más…

Definir las siguientes funciones

pares  :: Integer -> Integer -> [(Integer,Integer)]
nPares :: Integer -> Integer -> Integer

tales que

• (pares a b) es la lista de los pares de números enteros positivos tales que su máximo común divisor es a y su mínimo común múltiplo es b. Por ejemplo,

pares 3 3  == [(3,3)]
pares 4 12 == [(4,12),(12,4)]
pares 2 12 == [(2,12),(4,6),(6,4),(12,2)]
pares 2 60 == [(2,60),(4,30),(6,20),(10,12),(12,10),(20,6),(30,4),(60,2)]
pares 2 7  == []
pares 12 3  ==  []
length (pares 3 (product [3,5..91]))  ==  8388608

• (nPares a b) es el número de pares de enteros positivos tales que su máximo común divisor es a y su mínimo común múltiplo es b. Por ejemplo,

nPares 3 3   ==  1
nPares 4 12  ==  2
nPares 2 12  ==  4
nPares 2 60  ==  8
nPares 2 7   ==  0
nPares 12 3  ==  0
nPares 3 (product [3..3*10^4]) `mod` (10^12)  ==  477999992832
length (show (nPares 3 (product [3..3*10^4])))  ==  977

Leer más…

Las expresiones aritméticas se pueden representar como árboles con números en las hojas y operaciones en los nodos. Por ejemplo, la expresión "9-2*4" se puede representar por el árbol

  -
 / \
9   *
   / \
  2   4

Definiendo el tipo de dato Arbol por

data Arbol = H Int | N (Int -> Int -> Int) Arbol Arbol

la representación del árbol anterior es

N (-) (H 9) (N (*) (H 2) (H 4))

Definir la función

valor :: Arbol -> Int

tal que (valor a) es el valor de la expresión aritmética correspondiente al árbol a. Por ejemplo,

valor (N (-) (H 9) (N (*) (H 2) (H 4)))    ==  1
valor (N (+) (H 9) (N (*) (H 2) (H 4)))    ==  17
valor (N (+) (H 9) (N (div) (H 4) (H 2)))  ==  11
valor (N (+) (H 9) (N (max) (H 4) (H 2)))  ==  13

Leer más…

Un número semiprimo es un número natural que es producto de dos números primos no necesariamente distintos. Por ejemplo, 26 es semiprimo (porque 26 = 2 x 13) y 49 también lo es (porque 49 = 7 x 7).

Definir la función

mayorSemiprimoMenor :: Integer -> Integer

tal que (mayorSemiprimoMenor n) es el mayor semiprimo menor que n (suponiendo que n > 4). Por ejemplo,

mayorSemiprimoMenor 27      ==  26
mayorSemiprimoMenor 50      ==  49
mayorSemiprimoMenor 49      ==  46
mayorSemiprimoMenor (10^6)  ==  999997

Leer más…

Una forma de aproximar el número π es usando la siguiente igualdad:

 π         1     1*2     1*2*3     1*2*3*4
--- = 1 + --- + ----- + ------- + --------- + ....
 2         3     3*5     3*5*7     3*5*7*9

Es decir, la serie cuyo término general n-ésimo es el cociente entre el producto de los primeros n números y los primeros n números impares:

            Π i
s(n) =  -----------
         Π (2*i+1)

Definir la función

aproximaPi :: Double -> Double

tal que (aproximaPi n) es la aproximación del número π calculada con la serie anterior hasta el término n-ésimo. Por ejemplo,

aproximaPi 10   ==  3.141106021601377
aproximaPi 30   ==  3.1415926533011587
aproximaPi 50   ==  3.1415926535897922

Leer más…

La suma de los primos menores que 10 es 2 + 3 + 5 + 7 = 17.

Definir la función

sumaPrimosMenores :: Integer -> Integer

tal que (sumaPrimosMenores n) es la suma de los primos menores que n. Por ejemplo,

sumaPrimosMenores 10        ==  17
sumaPrimosMenores (5*10^5)  ==  9914236195

Nota: Este ejercicio está basado en el problema 10 del Proyecto Euler

Leer más…

Definir la constante

primosOcuadradosDePrimos :: [Integer]

cuyos elementos son los número primos o cuadrados de primos. Por ejemplo,

λ> take 20 primosOcuadradosDePrimos
[2,3,4,5,7,9,11,13,17,19,23,25,29,31,37,41,43,47,49,53]

Comprobar con QuickCheck que las lista primosOcuadradosDePrimos y unifactorizables (definida en el ejercicio anterior) son iguales.

Leer más…

Definir las funciones

sublistasConProducto :: Integer -> [Integer] -> [[Integer]]
unifactorizables :: [Integer]

tales que

• (sublistasConProducto n xs) es la lista de las sublistas de la lista ordenada estrictamente creciente xs (cuyos elementos son enteros mayores que 1) cuyo producto es el número entero n (con n mayor que 1). Por ejemplo,

λ> sublistasConProducto 72 [2,3,4,5,6,7,9,10,16]
[[2,4,9],[3,4,6]]
λ> sublistasConProducto 720 [2,3,4,5,6,7,9,10,16]
[[2,3,4,5,6],[2,4,9,10],[3,4,6,10],[5,9,16]]
λ> sublistasConProducto 2 [4,7]
[]
λ> length (sublistasConProducto 1234567 [1..1234567])
4

• unifactorizables es la lísta de los números enteros mayores que 1 que se pueden escribir sólo de una forma única como producto de enteros distintos mayores que uno. Por ejemplo,

λ> take 20 unifactorizables
[2,3,4,5,7,9,11,13,17,19,23,25,29,31,37,41,43,47,49,53]
λ> unifactorizables !! 300
1873

Leer más…

La sucesión de los números triangulares se obtiene sumando los números naturales. Así, los 8 primeros números triangulares son

 1 = 1
 3 = 1+2
 6 = 1+2+3
10 = 1+2+3+4
15 = 1+2+3+4+5
21 = 1+2+3+4+5+6
28 = 1+2+3+4+5+6+7
36 = 1+2+3+4+5+6+7+8

Para cada número triangular n existen números naturales a y b, tales que a . n + b también es triangular. Para n = 6, se tiene que

 6 = 1 * 6 + 0
15 = 2 * 6 + 3
21 = 3 * 6 + 3
28 = 4 * 6 + 4
36 = 5 * 6 + 5

son números triangulares

Definir la función

transformaciones :: Integer -> [(Integer,Integer)]

tal que si n es triangular, (transformaciones n) es la lista de los pares (a,b) tales que a es un entero positivo y b el menor número tal que a . n + b es triangular. Por ejemplo,

take 5 (transformaciones 6)  == [(1,0),(2,3),(3,3),(4,4),(5,6)]
take 5 (transformaciones 15) == [(1,0),(2,6),(3,10),(4,6),(5,3)]
transformaciones 21 !! (7*10^7) == (70000001,39732)

Leer más…

Se observa que todos los primeros números naturales tienen al menos un múltiplo no nulo que está formado solamente por ceros y unos. Por ejemplo, 1x10=10, 2x5=10, 3x37=111, 4x25=100, 5x2=10, 6x185=1110; 7x143=1001; 8X125=1000; 9x12345679=111111111.

Definir la función

multiplosCon1y0 :: Integer -> [Integer]

tal que (multiplosCon1y0 n) es la lista de los múltiplos de n cuyos dígitos son 1 ó 0. Por ejemplo,

take 4 (multiplosCon1y0 3)      ==  [111,1011,1101,1110]
take 3 (multiplosCon1y0 23)     ==  [110101,1011011,1101010]
head (multiplosCon1y0 1234658)  ==  110101101101000000110

Comprobar con QuickCheck que todo entero positivo tiene algún múltiplo cuyos dígitos son 1 ó 0.

Leer más…

Los números 545, 5995 y 15151 son los tres menores palíndromos (capicúas) que son divisibles por 109.

Definir las funciones

multiplosPalindromos :: Integer -> [Integer]
multiplosPalindromosMenores :: Integer -> Integer -> [Integer]

tales que

• (multiplosPalindromos n) es la lista de los palíndromos divisibles por n. Por ejemplo,

take 5 (multiplosPalindromos 109) == [545,5995,15151,64746,74447]

• (multiplosPalindromosMenoresx n) es la lista de los palíndromos divisibles por n, menores que x. Por ejemplo,

λ> multiplosPalindromosMenores (10^5) 109
[545,5995,15151,64746,74447,79897,84148,89598,99299]

Nota: Este ejercicio está basado en el problema 655 del Proyecto Euler.

Leer más…

Definir la función

mayorProducto :: Int -> Integer -> Integer

tal que (mayorProducto n x) es el mayor producto de n dígitos consecutivos del número x (suponiendo que x tiene al menos n dígitos). Por ejemplo,

mayorProducto 2 325                  ==  10
mayorProducto 5 11111                ==  1
mayorProducto 5 113111               ==  3
mayorProducto 5 110111               ==  0
mayorProducto 5 10151112             ==  10
mayorProducto 5 101511124            ==  10
mayorProducto 5 (product [1..1000])  ==  41472

Nota: Este ejercicio está basado en el problema 8 del Proyecto Euler

Leer más…

Definir la función

menorDivisible :: Integer -> Integer -> Integer

tal que (menorDivisible a b) es el menor número divisible por todos los números desde a hasta b, ambos inclusive. Por ejemplo,

menorDivisible 1 10                         ==  2520
length (show (menorDivisible6 1 (3*10^5)))  ==  130141

Nota: Este ejercicio está basado en el problema 5 del Proyecto Euler

Leer más…

La sucesión de los números triangulares se obtiene sumando los números naturales.

*     *      *        *         *
     * *    * *      * *       * *
           * * *    * * *     * * *
                   * * * *   * * * *
                            * * * * *
1     3      6        10        15

Así, el 7º número triangular es

1 + 2 + 3 + 4 + 5 + 6 + 7 = 28.

Los primeros 10 números triangulares son

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

Los divisores de los primeros 7 números triangulares son:

 1: 1
 3: 1,3
 6: 1,2,3,6
10: 1,2,5,10
15: 1,3,5,15
21: 1,3,7,21
28: 1,2,4,7,14,28

Como se puede observar, 28 es el menor número triangular con más de 5 divisores.

Definir la función

menorTriangularConAlMenosNDivisores :: Int -> Integer

tal que (menorTriangularConAlMenosNDivisores n) es el menor número triangular que tiene al menos n divisores. Por ejemplo,

menorTriangularConAlMenosNDivisores 5    ==  28
menorTriangularConAlMenosNDivisores 50   ==  25200
menorTriangularConAlMenosNDivisores 500  ==  76576500

Nota: Este ejercicio está basado en el problema 12 del Proyecto Euler

Leer más…

Los divisores primos de 13195 son 5, 7, 13 y 29. Por tanto, el mayor divisor primo de 13195 es 29.

Definir la función

mayorDivisorPrimo :: Integer -> Integer

tal que (mayorDivisorPrimo n) es el mayor divisor primo de n. Por ejemplo,

mayorDivisorPrimo 13195            ==  29
mayorDivisorPrimo 152416333181401  ==  12345701

Nota: Este ejercicio está basado en el problema 3 del Proyecto Euler

Leer más…

La sucesión de los números triangulares se obtiene sumando los números naturales.

*     *      *        *         *
     * *    * *      * *       * *
           * * *    * * *     * * *
                   * * * *   * * * *
                            * * * * *
1     3      6        10        15

Así, los 5 primeros números triangulares son

 1 = 1
 3 = 1+2
 6 = 1+2+3
10 = 1+2+3+4
15 = 1+2+3+4+5

Definir la función

triangulares :: [Integer]

tal que triangulares es la lista de los números triangulares. Por ejemplo,

take 10 triangulares  ==  [1,3,6,10,15,21,28,36,45,55]
maximum (take (5*10^6) triangulares4)  ==  12500002500000

Comprobar con QuickCheck que entre dos números triangulares consecutivos siempre hay un número primo.

Leer más…

Definir la función

sumaDivisores :: Integer -> Integer

tal que (sumaDivisores x) es la suma de los divisores de x. Por ejemplo,

sumaDivisores 12  ==  28
sumaDivisores 25  ==  31
sumaDivisores (product [1..25])  ==  93383273455325195473152000
length (show (sumaDivisores (product [1..30000])))  ==  121289
maximum (map sumaDivisores2 [1..10^5])  ==  403200

Leer más…

La descomposición prima de 600 es

600 = 2³ * 3 * 5²

Definir la función

factorizacion :: Integer -> [(Integer,Integer)]

tal que (factorizacion x) ses la lista de las bases y exponentes de la descomposición prima de x. Por ejemplo,

factorizacion 600  ==  [(2,3),(3,1),(5,2)]
length (factorizacion (product [1..3*10^4]))  ==  3245

Leer más…

Definir la función

numeroDivisores :: Integer -> Integer

tal que (numeroDivisores x) es el número de divisores de x. Por ejemplo,

numeroDivisores 12  ==  6
numeroDivisores 25  ==  3
length (show (numeroDivisores (product [1..3*10^4])))  ==  1948

Leer más…

Definir la función

divisores :: Integer -> [Integer]

tal que (divisores x) es el conjunto de divisores de los x. Por ejemplo,

divisores 30  ==  [1,2,3,5,6,10,15,30]
length (divisores (product [1..10]))  ==  270
length (divisores (product [1..25]))  ==  340032

Leer más…

Definir la función

producto :: [[a]] -> [[a]]

tal que (producto xss) es el producto cartesiano de los conjuntos xss. Por ejemplo,

λ> producto [[1,3],[2,5]]
[[1,2],[1,5],[3,2],[3,5]]
λ> producto [[1,3],[2,5],[6,4]]
[[1,2,6],[1,2,4],[1,5,6],[1,5,4],[3,2,6],[3,2,4],[3,5,6],[3,5,4]]
λ> producto [[1,3,5],[2,4]]
[[1,2],[1,4],[3,2],[3,4],[5,2],[5,4]]
λ> producto []
[[]]

Comprobar con QuickCheck que para toda lista de listas de números enteros, xss, se verifica que el número de elementos de (producto xss) es igual al producto de los números de elementos de cada una de las listas de xss.

Nota. Al hacer la comprobación limitar el tamaño de las pruebas como se indica a continuación

quickCheckWith (stdArgs {maxSize=9}) prop_producto

Leer más…

Definir la función

mayorPrefijoComun :: Eq a => [a] -> [a] -> [a]

tal que (mayorPrefijoComun xs ys) calcula el mayor prefijo común a xs e ys. Por ejemplo,

mayorPrefijoComun "masa" "madre"       == "ma"
mayorPrefijoComun "masa" "padre"       == ""
mayorPrefijoComun "hola" "hielo"       == "h"
mayorPrefijoComun "helado" "heladeria" == "helad"

Leer más…

Definir la función

listasDecrecientesDesde :: Int -> [[Int]]

tal que (listasDecrecientesDesde n) es la lista de las sucesiones estrictamente decrecientes cuyo primer elemento es n. Por ejemplo,

λ> listasDecrecientesDesde 2
[[2],[2,1],[2,1,0],[2,0]]
λ> listasDecrecientesDesde 3
[[3],[3,2],[3,2,1],[3,2,1,0],[3,2,0],[3,1],[3,1,0],[3,0]]

Leer más…

Leer más…

El factorial de 7 es

7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040

por tanto, el último dígito no nulo del factorial de 7 es 4.

Definir la función

ultimoNoNuloFactorial :: Integer -> Integer

tal que (ultimoNoNuloFactorial n) es el último dígito no nulo del factorial de n. Por ejemplo,

ultimoNoNuloFactorial  7  == 4
ultimoNoNuloFactorial 10  == 8
ultimoNoNuloFactorial 12  == 6
ultimoNoNuloFactorial 97  == 2
ultimoNoNuloFactorial  0  == 1

Comprobar con QuickCheck que si n es mayor que 4, entonces el último dígito no nulo del factorial de n es par.

Leer más…

Dos números enteros son primos relativos si no tienen ningún factor primo en común, o, dicho de otra manera, si no tienen otro divisor común más que 1 y -1. Equivalentemente son primos entre sí, si y sólo si, su máximo común divisor es igual a 1.

Por ejemplo, 6 y 35 son primos entre sí, pero 6 y 27 no lo son porque ambos son divisibles por 3

Definir la función

primosRelativos :: [Int] -> Bool

tal que (primosRelativos xs) se verifica si los elementos de xs son primos relativos dos a dos. Por ejemplo,

primosRelativos [6,35]         ==  True
primosRelativos [6,27]         ==  False
primosRelativos [2,3,4]        ==  False
primosRelativos [6,35,11]      ==  True
primosRelativos [6,35,11,221]  ==  True
primosRelativos [6,35,11,231]  ==  False

Leer más…

Los números de Perrin se definen por la elación de recurrencia

P(n) = P(n - 2) + P(n - 3) si n > 2,

con los valores iniciales

P(0) = 3, P(1) = 0 y P(2) = 2.

Definir la sucesión

sucPerrin :: [Integer]

cuyos elementos son los números de Perrin. Por ejemplo,

λ> take 15 sucPerrin
[3,0,2,3,2,5,5,7,10,12,17,22,29,39,51]
λ> length (show (sucPerrin !! (2*10^5)))
24425

Comprobar con QuickCheck si se verifica la siguiente propiedad: para todo entero n > 1, el n-ésimo término de la sucesión de Perrin es divisible por n si y sólo si n es primo.

Leer más…

La sucesión fractal

0, 0, 1, 0, 2, 1, 3, 0, 4, 2, 5, 1, 6, 3, 7, 0, 8, 4, 9, 2,
10, 5, 11, 1, 12, 6, 13, 3, 14, 7, 15, ...

está construida de la siguiente forma:

• los términos pares forman la sucesión de los números naturales

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ...

• los términos impares forman la misma sucesión original

0, 0, 1, 0, 2, 1, 3, 0, 4, 2, 5, 1, 6, 3, 7, ...

Definir las funciones

sucFractal     :: [Integer]
sumaSucFractal :: Integer -> Integer

tales que

• sucFractal es la lista de los términos de la sucesión fractal. Por ejemplo,

take 20 sucFractal   == [0,0,1,0,2,1,3,0,4,2,5,1,6,3,7,0,8,4,9,2]
sucFractal !! 30     == 15
sucFractal !! (10^7) == 5000000

• (sumaSucFractal n) es la suma de los n primeros términos de la sucesión fractal. Por ejemplo,

sumaSucFractal 10      == 13
sumaSucFractal (10^5)  == 1666617368
sumaSucFractal (10^10) == 16666666661668691669
sumaSucFractal (10^15) == 166666666666666166673722792954
sumaSucFractal (10^20) == 1666666666666666666616666684103392376198
length (show (sumaSucFractal (10^15000))) == 30000
sumaSucFractal (10^15000) `mod` (10^9)    == 455972157

Leer más…

El menor número con 2¹ divisores es el 2, ya que tiene 2 divisores (el 1 y el 2) y el anterior al 2 (el 1) sólo tiene 1 divisor (el 1).

El menor número con 2² divisores es el 6, ya que tiene 4 divisores (el 1, 2, 3 y 6) y sus anteriores (el 1, 2, 3, 4 y 5) tienen menos de 4 divisores (tienen 1, 1, 1, 3 y 1, respectivamente).

El menor número con 2³ divisores es el 24, ya que tiene 8 divisores (el 1, 2, 3, 4, 6, 8, 12 y 24) y sus anteriores (del 1 al 23) tienen menos de 8 divisores.

El menor número con 16 divisores es el 120, ya que tiene 16 divisores (el 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 y 120) y sus anteriores (del 1 al 119) tienen menos de 16 divisores.

El menor número, módulo 100, con 16 divisores es el 20, ya que el menor número con 16 divisores es el 120 y 120 módulo 100 es 20.

Definir la función

menor :: Integer -> Integer -> Integer

tal que (menor n m) es el menor número, módulo m, con 2^n divisores. Por ejemplo,

menor 4 1000                    ==  120
menor 4 100                     ==  20
[menor n (10^9) | n <- [1..8]]  ==  [2,6,24,120,840,7560,83160,1081080]
menor 500500 500500506          ==  8728302

Leer más…

En el episodio número 73 de la serie The Big Bang Theory, Sheldon Cooper enuncia lo siguiente:

«El mejor número es el 73. El 73 es el 21-ésimo número primo. Al invertir sus cifras obtenemos 37, que es el primo número 12. Y al invertir este obtenemos 21, que es el producto de ─agarraos fuerte─ 7 y 3.»

Se define un número primo de Sheldon como: el n-ésimo número primo p(n) será un primo de Sheldon si cumple que el producto de sus dígitos es n y si, además, el número que se obtiene al invertir sus cifras, rev(p(n)), es el rev(n)-ésimo número primo; es decir, si rev(p(n)) = p(rev(n)).

Definir la función

esPrimoSheldon :: Int -> Bool

tal que (esPrimoSheldon x) se verifica si x un primo de Sheldon. Por ejemplo,

esPrimoSheldon 73  ==  True
esPrimoSheldon 79  ==  False

Comprobar con QuickCheck que 73 es el único primo de Sheldon.

Leer más…

Los números de Fibonacci se definen mediante las ecuaciones

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2), si n > 1

Los primeros números de Fibonacci son

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...

Una generalización de los anteriores son los números de Pentanacci definidos por las siguientes ecuaciones

P(0) = 0
P(1) = 1
P(2) = 1
P(3) = 2
P(4) = 4
P(n) = P(n-1) + P(n-2) + P(n-3) + P(n-4) + P(n-5), si n > 4

Los primeros números de Pentanacci son

0, 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, ...

Definir la sucesión

pentanacci :: [Integer]

cuyos elementos son los números de Pentanacci. Por ejemplo,

λ> take 15 pentanacci
[0,1,1,2,4,8,16,31,61,120,236,464,912,1793,3525]
λ> (pentanacci !! (10^5)) `mod` (10^30)
482929150584077921552549215816
231437922897686901289110700696
λ> length (show (pentanacci !! (10^5)))
29357

Leer más…

Leer más…

En la Olimpiada Internacional de Matemáticas del 2012 se propuso el siguiente problema:

Varios enteros positivos se escriben en una lista. Iterativamente, Alicia elige dos números adyacentes x e y tales que x > y y x está a la izquierda de y y reemplaza el par (x,y) por (y+1,x) o (x-1,x). Demostrar que sólo puede aplicar un número finito de dichas iteraciones.

Por ejemplo, las transformadas de la lista [1,3,2] son [1,2,3] y [1,3,3] y las dos obtenidas son finales (es decir, no se les puede aplicar ninguna transformación).

Definir las funciones

soluciones :: [Int] -> [Estado]
finales :: [Int] -> [[Int]]
finalesMaximales :: [Int] -> (Int,[[Int]])

tales que

• (soluciones xs) es la lista de pares (n,ys) tales que ys es una lista final obtenida aplicándole n transformaciones a xs. Por ejemplo,

λ> soluciones [1,3,2]
[(1,[1,3,3]),(1,[1,2,3])]
λ> sort (nub (soluciones [3,3,2]))
[(1,[3,3,3]),(2,[2,3,3]),(2,[3,3,3])]
λ> sort (nub (soluciones [3,2,1]))
[(2,[2,2,3]),(3,[2,2,3]),(3,[2,3,3]),(3,[3,3,3]),(4,[2,3,3]),(4,[3,3,3])]

• (finales xs) son las listas obtenidas transformando xs y a las que no se les puede aplicar más transformaciones. Por ejemplo,

finales [1,2,3]               ==  [[1,2,3]]
finales [1,3,2]               ==  [[1,2,3],[1,3,3]]
finales [3,2,1]               ==  [[2,2,3],[2,3,3],[3,3,3]]
finales [1,3,2,4]             ==  [[1,2,3,4],[1,3,3,4]]
finales [1,3,2,3]             ==  [[1,2,3,3],[1,3,3,3]]
length (finales [9,6,0,7,2])  ==  19
length (finales [80,60..0])   ==  420

• (finalesMaximales xs) es el par (n,yss) tal que la longitud de las cadenas más largas de transformaciones a partir de xs e yss es la lista de los estados finales a partir de xs con n transformaciones. Por ejemplo,

finalesMaximales [9,5,7]   ==  (2,[[6,8,9],[8,8,9]])
finalesMaximales [3,2,1]   ==  (4,[[2,3,3],[3,3,3]])
finalesMaximales [3,2..0]  ==  (10,[[2,3,3,3],[3,3,3,3]])
finalesMaximales [4,3..0]  ==  (20,[[3,4,4,4,4],[4,4,4,4,4]])

Leer más…

Definir las funciones

grafo   :: [(Int,Int)] -> Grafo Int Int
caminos :: Grafo Int Int -> Int -> Int -> [[Int]]

tales que

• (grafo as) es el grafo no dirigido definido cuyas aristas son as. Por ejemplo,

λ> grafo [(2,4),(4,5)]
G ND (array (2,5) [(2,[(4,0)]),(3,[]),(4,[(2,0),(5,0)]),(5,[(4,0)])])

• (caminos g a b) es la lista los caminos en el grafo g desde a hasta b sin pasar dos veces por el mismo nodo. Por ejemplo,

λ> sort (caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 1 7)
[[1,3,5,7],[1,3,7]]
λ> sort (caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 2 7)
[[2,5,3,7],[2,5,7]]
λ> sort (caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 1 2)
[[1,3,5,2],[1,3,7,5,2]]
λ> caminos (grafo [(1,3),(2,5),(3,5),(3,7),(5,7)]) 1 4
[]
λ> length (caminos (grafo [(i,j) | i <- [1..10], j <- [i..10]]) 1 10)
109601

Leer más…

Una triangulación de un polígono es una división del área en un conjunto de triángulos, de forma que la unión de todos ellos es igual al polígono original, y cualquier par de triángulos es disjunto o comparte únicamente un vértice o un lado. En el caso de polígonos convexos, la cantidad de triangulaciones posibles depende únicamente del número de vértices del polígono.

Si llamamos T(n) al número de triangulaciones de un polígono de n vértices, se verifica la siguiente relación de recurrencia:

T(2) = 1
T(n) = T(2)*T(n-1) + T(3)*T(n-2) + ... + T(n-1)*T(2)

Definir la función

numeroTriangulaciones :: Integer -> Integer

tal que (numeroTriangulaciones n) es el número de triangulaciones de un polígono convexo de n vértices. Por ejemplo,

numeroTriangulaciones 3  == 1
numeroTriangulaciones 5  == 5
numeroTriangulaciones 6  == 14
numeroTriangulaciones 7  == 42
numeroTriangulaciones 50 == 131327898242169365477991900
length (show (numeroTriangulaciones   800)) ==  476
length (show (numeroTriangulaciones  1000)) ==  597
length (show (numeroTriangulaciones 10000)) == 6014

Leer más…

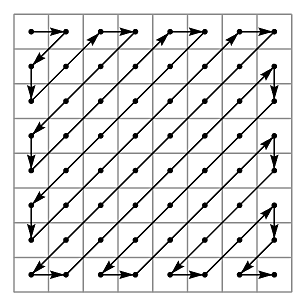
El problema de las N reinas consiste en colocar N reinas en tablero rectangular de dimensiones N por N de forma que no se encuentren más de una en la misma línea: horizontal, vertical o diagonal. Por ejemplo, una solución para el problema de las 4 reinas es

|---|---|---|---|
|   | R |   |   |
|---|---|---|---|
|   |   |   | R |
|---|---|---|---|
| R |   |   |   |
|---|---|---|---|
|   |   | R |   |
|---|---|---|---|

Los estados del problema de las N reinas son los tableros con las reinas colocadas. Inicialmente el tablero está vacío y, en cda paso se coloca una reina en la primera columna en la que aún no hay ninguna reina.

Cada estado se representa por una lista de números que indican las filas donde se han colocado las reinas. Por ejemplo, el tablero anterior se representa por [2,4,1,3].

Usando la librería de árboles Data.Tree, definir las funciones

arbolReinas :: Int -> Tree [Int]
nEstados    :: Int -> Int
soluciones  :: Int -> [[Int]]
nSoluciones :: Int -> Int

tales que

• (arbolReinas n) es el árbol de estados para el problema de las n reinas. Por ejemplo,

λ> putStrLn (drawTree (fmap show (arbolReinas 4)))
[]
|
+- [1]
|  |
|  +- [3,1]
|  |
|  `- [4,1]
|     |
|     `- [2,4,1]
|
+- [2]
|  |
|  `- [4,2]
|     |
|     `- [1,4,2]
|        |
|        `- [3,1,4,2]
|
+- [3]
|  |
|  `- [1,3]
|     |
|     `- [4,1,3]
|        |
|        `- [2,4,1,3]
|
`- [4]
   |
   +- [1,4]
   |  |
   |  `- [3,1,4]
   |
   `- [2,4]

λ> putStrLn (drawTree (fmap show (arbolReinas 5)))
[]
|
+- [1]
|  |
|  +- [3,1]
|  |  |
|  |  `- [5,3,1]
|  |     |
|  |     `- [2,5,3,1]
|  |        |
|  |        `- [4,2,5,3,1]
|  |
|  +- [4,1]
|  |  |
|  |  `- [2,4,1]
|  |     |
|  |     `- [5,2,4,1]
|  |        |
|  |        `- [3,5,2,4,1]
|  |
|  `- [5,1]
|     |
|     `- [2,5,1]
|
+- [2]
|  |
|  +- [4,2]
|  |  |
|  |  `- [1,4,2]
|  |     |
|  |     `- [3,1,4,2]
|  |        |
|  |        `- [5,3,1,4,2]
|  |
|  `- [5,2]
|     |
|     +- [1,5,2]
|     |  |
|     |  `- [4,1,5,2]
|     |
|     `- [3,5,2]
|        |
|        `- [1,3,5,2]
|           |
|           `- [4,1,3,5,2]
|
+- [3]
|  |
|  +- [1,3]
|  |  |
|  |  `- [4,1,3]
|  |     |
|  |     `- [2,4,1,3]
|  |        |
|  |        `- [5,2,4,1,3]
|  |
|  `- [5,3]
|     |
|     `- [2,5,3]
|        |
|        `- [4,2,5,3]
|           |
|           `- [1,4,2,5,3]
|
+- [4]
|  |
|  +- [1,4]
|  |  |
|  |  +- [3,1,4]
|  |  |  |
|  |  |  `- [5,3,1,4]
|  |  |     |
|  |  |     `- [2,5,3,1,4]
|  |  |
|  |  `- [5,1,4]
|  |     |
|  |     `- [2,5,1,4]
|  |
|  `- [2,4]
|     |
|     `- [5,2,4]
|        |
|        `- [3,5,2,4]
|           |
|           `- [1,3,5,2,4]
|
`- [5]
   |
   +- [1,5]
   |  |
   |  `- [4,1,5]
   |
   +- [2,5]
   |  |
   |  `- [4,2,5]
   |     |
   |     `- [1,4,2,5]
   |        |
   |        `- [3,1,4,2,5]
   |
   `- [3,5]
      |
      `- [1,3,5]
         |
         `- [4,1,3,5]
            |
            `- [2,4,1,3,5]

• (nEstados n) es el número de estados en el problema de las n reinas. Por ejemplo,

nEstados 4            ==  17
nEstados 5            ==  54
map nEstados [0..10]  ==  [1,2,3,6,17,54,153,552,2057,8394,35539]

• (soluciones n) es la lista de estados que son soluciones del problema de las n reinas. Por ejemplo,

λ> soluciones 4
[[3,1,4,2],[2,4,1,3]]
λ> soluciones 5
[[4,2,5,3,1],[3,5,2,4,1],[5,3,1,4,2],[4,1,3,5,2],[5,2,4,1,3],
 [1,4,2,5,3],[2,5,3,1,4],[1,3,5,2,4],[3,1,4,2,5],[2,4,1,3,5]]

• (nSoluciones n) es el número de soluciones del problema de las n reinas. Por ejemplo,

nSoluciones 4            ==  2
nSoluciones 5            ==  10
map nSoluciones [0..10]  ==  [1,1,0,0,2,10,4,40,92,352,724]

Leer más…

El problema de las N torres consiste en colocar N torres en un tablero con N filas y N columnas de forma que no haya dos torres en la misma fila ni en la misma columna.

Cada solución del problema de puede representar mediante una matriz con ceros y unos donde los unos representan las posiciones ocupadas por las torres y los ceros las posiciones libres. Por ejemplo,

( 0 1 0 )
( 1 0 0 )
( 0 0 1 )

representa una solución del problema de las 3 torres.

Definir las funciones

torres  :: Int -> [Matrix Int]
nTorres :: Int -> Integer

tales que

• (torres n) es la lista de las soluciones del problema de las n torres. Por ejemplo,

λ> torres 3
[( 1 0 0 )
 ( 0 1 0 )
 ( 0 0 1 )
 ,( 1 0 0 )
 ( 0 0 1 )
 ( 0 1 0 )
 ,( 0 1 0 )
 ( 1 0 0 )
 ( 0 0 1 )
 ,( 0 1 0 )
 ( 0 0 1 )
 ( 1 0 0 )
 ,( 0 0 1 )
 ( 1 0 0 )
 ( 0 1 0 )
 ,( 0 0 1 )
 ( 0 1 0 )
 ( 1 0 0 )
]

donde se ha indicado con 1 las posiciones ocupadas por las torres.

• (nTorres n) es el número de soluciones del problema de las n torres. Por ejemplo,

λ> nTorres 3
6
λ> length (show (nTorres (10^4)))
35660

Leer más…

Dado un grafo no dirigido G, un camino en G es una secuencia de nodos [v(1),v(2),v(3),...,v(n)] tal que para todo i entre 1 y n-1, (v(i),v(i+1)) es una arista de G. Por ejemplo, dados los grafos

g1, g2 :: Grafo Int Int
g1 = creaGrafo ND (1,3) [(1,2,0),(1,3,0),(2,3,0)]
g2 = creaGrafo ND (1,4) [(1,2,0),(1,3,0),(1,4,0),(2,4,0),(3,4,0)]

la lista [1,2,3] es un camino en g1, pero no es un camino en g2 puesto que la arista (2,3) no existe en g2.

Definir la función

camino :: Grafo Int Int -> [Int] -> Bool

tal que (camino g vs) se verifica si la lista de nodos vs es un camino en el grafo g. Por ejemplo,

camino g1 [1,2,3]  ==  True
camino g2 [1,2,3]  ==  False

Nota: Este ejercicio debe realizarse usando únicamente las funciones de la librería de grafos (I1M.Grafo) que se describe aquí y se encuentra aquí.

Leer más…

Definir la función

frecuencias :: Ord a => [a] -> Map a Int

tal que (frecuencias xs) es el diccionario formado por los elementos de xs junto con el número de veces que aparecen en xs. Por ejemplo,

λ> frecuencias "sosos"
fromList [('o',2),('s',3)]
λ> frecuencias (show (10^100))
fromList [('0',100),('1',1)]
λ> frecuencias (take (10^6) (cycle "abc"))
fromList [('a',333334),('b',333333),('c',333333)]
λ> size (frecuencias (take (10^6) (cycle [1..10^6])))
1000000

Leer más…

B₀(x) = 1 (polinomio unidad)
Bₙ(x) = x·[Bₙ(x) + Bₙ'(x)]

Por ejemplo,

B₀(x) = 1                     = 1
B₁(x) = x·(1+0)               = x
B₂(x) = x·(x+1)               = x²+x
B₃(x) = x·(x²+x+2x+1)         = x³+3x²+x
B₄(x) = x·(x³+3x²+x+3x²+6x+1) = x⁴+6x³+7x²+x

Definir la función

polBell :: Integer -> Polinomio Integer

tal que (polBell n) es el polinomio de Bell de grado n. Por ejemplo,

polBell 4                    ==  x^4 + 6*x^3 + 7*x^2 + 1*x
coeficiente 2 (polBell 4)    ==  7
coeficiente 2 (polBell 30)   ==  536870911
coeficiente 1 (polBell 1000) == 1
length (show (coeficiente 9 (polBell 1000)))  ==  949

Notas: Se usa la librería I1M.PolOperaciones que se encuentra aquí y se describe aquí. Además, en el último ejemplo se usa la función coeficiente tal que (coeficiente k p) es el coeficiente del término de grado k en el polinomio p definida por

coeficiente :: Num a => Int -> Polinomio a -> a
coeficiente k p | k == n                 = coefLider p
                | k > grado (restoPol p) = 0
                | otherwise              = coeficiente k (restoPol p)
                where n = grado p

Leer más…

Empezando con el número 1 y moviéndose en el sentido de las agujas del reloj se obtienen las matrices espirales

|1 2|   |7 8 9|   | 7  8  9 10|   |21 22 23 24 25|
|4 3|   |6 1 2|   | 6  1  2 11|   |20  7  8  9 10|
        |5 4 3|   | 5  4  3 12|   |19  6  1  2 11|
                  |16 15 14 13|   |18  5  4  3 12|
                                  |17 16 15 14 13|

La suma los elementos de sus diagonales es

+ en la 2x2: 1+3+2+4               =  10
+ en la 3x3: 1+3+5+7+9             =  25
+ en la 4x4: 1+2+3+4+7+10+13+16    =  56
+ en la 5x5: 1+3+5+7+9+13+17+21+25 = 101

Definir la función

sumaDiagonales :: Integer -> Integer

tal que (sumaDiagonales n) es la suma de los elementos en las diagonales de la matriz espiral de orden nxn. Por ejemplo.

sumaDiagonales 1         ==  1
sumaDiagonales 2         ==  10
sumaDiagonales 3         ==  25
sumaDiagonales 4         ==  56
sumaDiagonales 5         ==  101
sumaDiagonales (10^6)    ==  666667166668000000
sumaDiagonales (1+10^6)  ==  666669166671000001

sumaDiagonales (10^2)  ==         671800
sumaDiagonales (10^3)  ==        667168000
sumaDiagonales (10^4)  ==       666716680000
sumaDiagonales (10^5)  ==      666671666800000
sumaDiagonales (10^6)  ==     666667166668000000
sumaDiagonales (10^7)  ==    666666716666680000000
sumaDiagonales (10^8)  ==   666666671666666800000000
sumaDiagonales (10^9)  ==  666666667166666668000000000

length (show (sumaDiagonales (10^(10^4))))  == 30000
length (show (sumaDiagonales (10^(10^5))))  == 300000
length (show (sumaDiagonales (10^(10^6))))  == 3000000

Comprobar con QuickCheck que el último dígito de (sumaDiagonales n) es 0, 4 ó 6 si n es par y es 1, 5 ó 7 en caso contrario.

Leer más…

Definir la funciones

sumas  :: Int -> [[Int]]
nSumas :: Int -> Integer

tales que

• (sumas n) es la lista de las descomposiciones de n como sumas cuyos sumandos son 1 ó 2. Por ejemplo,

sumas 1            ==  [[1]]
sumas 2            ==  [[1,1],[2]]
sumas 3            ==  [[1,1,1],[1,2],[2,1]]
sumas 4            ==  [[1,1,1,1],[1,1,2],[1,2,1],[2,1,1],[2,2]]
length (sumas 26)  ==  196418
length (sumas 33)  ==  5702887

• (nSumas n) es el número de descomposiciones de n como sumas cuyos sumandos son 1 ó 2. Por ejemplo,

nSumas 4                      ==  5
nSumas 123                    ==  36726740705505779255899443
length (show (nSumas 123456)) ==  25801

Leer más…

La matriz zizagueante de orden n es la matriz cuadrada con n filas y n columnas y cuyos elementos son los n² primeros números naturales colocados de manera creciente a lo largo de las diagonales secundarias. Por ejemplo, La matriz zigzagueante de orden 5 es

 0  1  5  6 14
 2  4  7 13 15
 3  8 12 16 21
 9 11 17 20 22
10 18 19 23 24

La colocación de los elementos se puede ver gráficamente en

Definir la función

zigZag :: Int -> Array (Int,Int) Int

tal que (zigZag n) es la matriz zigzagueante de orden n. Por ejemplo,

λ> elems (zigZag 3)
[0,1,5, 2,4,6, 3,7,8]
λ> elems (zigZag 4)
[0,1,5,6, 2,4,7,12, 3,8,11,13, 9,10,14,15]
λ> elems (zigZag 5)
[0,1,5,6,14, 2,4,7,13,15, 3,8,12,16,21, 9,11,17,20,22, 10,18,19,23,24]
λ> take 15 (elems (zigZag 1000))
[0,1,5,6,14,15,27,28,44,45,65,66,90,91,119]

Leer más…

La n-ésima densidad de un tipo de número es el cociente entre la cantidad de los números entre 1 y n que son del tipo considerado y n. Por ejemplo, la 7-ésima densidad de los múltiplos de 3 es 2/7 ya que entre los 7 primeros números sólo 2 son múltiplos de 3.

Definir las funciones

densidades :: Int -> (Double,Double,Double)
graficas   :: Imt -> IO ()

tales que

• (densidades n) es la terna formada por la n-ésima densidad de los números abundantes (es decir, para los que la suma de sus divisores propios es mayor que el número), de los números perfectos (es decir, para los que la suma de sus divisores propios es mayor que el número) y de los números deficientes (es decir, para los que la suma de sus divisores propios es menor que el número). Por ejemplo,

densidades 100     ==  (0.22,    2.0e-2, 0.76)
densidades 1000    ==  (0.246,   3.0e-3, 0.751)
densidades 10000   ==  (0.2488,  4.0e-4, 0.7508)
densidades 100000  ==  (0.24795, 4.0e-5, 0.75201)

• (graficas n) dibuja las gráficas de las k-ésimas densidades (para k entre 1 y n) de los números abundantes, de los números perfectos y de los números deficientes. Por ejemplo, (graficas 100) dibuja

y (graficas 400) dibuja

Leer más…

La sucesión de Loomis generada por un número entero positivo x es la sucesión cuyos términos se definen por

• f(0) es x
• f(n) es la suma de f(n-1) y el producto de los dígitos no nulos de f(n-1)

Los primeros términos de las primeras sucesiones de Loomis son

• Generada por 1: 1, 2, 4, 8, 16, 22, 26, 38, 62, 74, 102, 104, 108, 116, 122, ...
• Generada por 2: 2, 4, 8, 16, 22, 26, 38, 62, 74, 102, 104, 108, 116, 122, 126, ...
• Generada por 3: 3, 6, 12, 14, 18, 26, 38, 62, 74, 102, 104, 108, 116, 122, 126, ...
• Generada por 4: 4, 8, 16, 22, 26, 38, 62, 74, 102, 104, 108, 116, 122, 126, 138, ...
• Generada por 5: 5, 10, 11, 12, 14, 18, 26, 38, 62, 74, 102, 104, 108, 116, 122, ...

Se observa que a partir de un término todas coinciden con la generada por 1. Dicho término se llama el punto de convergencia. Por ejemplo,

• la generada por 2 converge a 2
• la generada por 3 converge a 26
• la generada por 4 converge a 4
• la generada por 5 converge a 26

Definir las siguientes funciones

sucLoomis           :: Integer -> [Integer]
convergencia        :: Integer -> Integer
graficaConvergencia :: [Integer] -> IO ()

tales que

• (sucLoomis x) es la sucesión de Loomis generada por x. Por ejemplo,

λ> take 15 (sucLoomis 1)
[1,2,4,8,16,22,26,38,62,74,102,104,108,116,122]
λ> take 15 (sucLoomis 2)
[2,4,8,16,22,26,38,62,74,102,104,108,116,122,126]
λ> take 15 (sucLoomis 3)
[3,6,12,14,18,26,38,62,74,102,104,108,116,122,126]
λ> take 15 (sucLoomis 4)
[4,8,16,22,26,38,62,74,102,104,108,116,122,126,138]
λ> take 15 (sucLoomis 5)
[5,10,11,12,14,18,26,38,62,74,102,104,108,116,122]
λ> take 15 (sucLoomis 20)
[20,22,26,38,62,74,102,104,108,116,122,126,138,162,174]
λ> take 15 (sucLoomis 100)
[100,101,102,104,108,116,122,126,138,162,174,202,206,218,234]
λ> sucLoomis 1 !! (2*10^5)
235180736652

• (convergencia x) es el término de convergencia de la sucesioń de Loomis generada por x xon la geerada por 1. Por ejemplo,

convergencia  2      ==  2
convergencia  3      ==  26
convergencia  4      ==  4
convergencia 17      ==  38
convergencia 19      ==  102
convergencia 43      ==  162
convergencia 27      ==  202
convergencia 58      ==  474
convergencia 63      ==  150056
convergencia 81      ==  150056
convergencia 89      ==  150056
convergencia (10^12) ==  1000101125092

• (graficaConvergencia xs) dibuja la gráfica de los términos de convergencia de las sucesiones de Loomis generadas por los elementos de xs. Por ejemplo, (graficaConvergencia ([1..50]) dibuja

y graficaConvergencia ([1..148] \ [63,81,89,137]) dibuja

Leer más…

Definir la función

mayorProducto :: Int -> Integer -> Integer

tal que (mayorProducto n x) es el mayor producto de n dígitos consecutivos del número x (suponiendo que x tiene al menos n dígitos). Por ejemplo,

mayorProducto 2 325                  ==  10
mayorProducto 5 11111                ==  1
mayorProducto 5 113111               ==  3
mayorProducto 5 110111               ==  0
mayorProducto 5 10151112             ==  10
mayorProducto 5 101511124            ==  10
mayorProducto 5 (product [1..1000])  ==  41472

Leer más…

Definir la función

productos :: Integer -> Integer -> [[Integer]]

tal que (productos n x) es las listas de n elementos consecutivos cuyo producto es x. Por ejemplo,

productos 2 6     ==  [[2,3]]
productos 3 6     ==  [[1,2,3]]
productos 4 1680  ==  [[5,6,7,8]]
productos 2 5     ==  []

Comprobar con QuickCheck que si n > 0 y x > 0, entonces

productos n (product [x..x+n-1]) == [[x..x+n-1]]

Usando productos, definir la función

productosDe2y3consecutivos :: [Integer]

cuyos elementos son los números naturales (no nulos) que pueden expresarse simultáneamente como producto de dos y tres números consecutivos. Por ejemplo,

head productosDe2y3consecutivos  ==  6

Nota. Según demostró Mordell en 1962, productosDe2y3consecutivos sólo tiene dos elementos.

Leer más…

Un segmento de una lista xs es una sublista de xs formada por elementos consecutivos en la lista. El problema de la máxima suma de segmentos consiste en dada una lista de números enteros calcular el máximo de las sumas de todos los segmentos de la lista. Por ejemplo, para la lista [-1,2,-3,5,-2,1,3,-2,-2,-3,6] la máxima suma de segmentos es 7 que es la suma del segmento [5,-2,1,3] y para la lista [-1,-2,-3] es 0 que es la suma de la lista vacía.

Definir la función

mss :: [Integer] -> Integer

tal que (mss xs) es la máxima suma de los segmentos de xs. Por ejemplo,

mss [-1,2,-3,5,-2,1,3,-2,-2,-3,6]  ==  7
mss [-1,-2,-3]                     ==  0
mss [1..500]                       ==  125250
mss [1..1000]                      ==  500500
mss [-500..3]                      ==  6
mss [-1000..3]                     ==  6

Leer más…

La conjetura de Waring sobre los números primos establece que todo número impar es primo o la suma de tres primos. La conjetura de Goldbach afirma que todo número par mayor que 2 es la suma de dos números primos. Ambos problemas ha estado abiertos durante más de 200 años. En este problema no se propone su solución, sino una tarea más simple: buscar una manera de expresar los enteros mayores que 7 como suma de exactamente cuatro números primos; es decir, definir la función

suma4primos :: Integer -> (Integer,Integer,Integer,Integer)

tal que (suma4primos n) es una cuádrupla (a,b,c,d) de números primos cuya suma es n (que se supone mayor que 7). Por ejemplo,

suma4primos 24             ==  (2,2,3,17)
suma4primos 1234567890123  ==  (2,3,29,1234567890089)

Comprobar con QuickCheck que suma4primos es correcta; es decir si (suma4primos n) es (a,b,c,d) entonces los números a, b c y d son primos y su suma es n.

Nota: Para cada n pueden existir distintas cuádruplas que cumplan la especificación. Por ejemplo, para el 16 hay tres: (2,2,5,7), (3,3,3,7) y (3,3,5,5). Cualquiera de ellas se admite como solución.

Leer más…

El período de una lista xs es la lista más corta ys tal que xs se puede obtener concatenando varias veces la lista ys. Por ejemplo, el período "abababab" es "ab" ya que "abababab" se obtiene repitiendo tres veces la lista "ab".

Definir la función

periodo :: Eq a => [a] -> [a]

tal que (periodo xs) es el período de xs. Por ejemplo,

periodo "ababab"      ==  "ab"
periodo "buenobueno"  ==  "bueno"
periodo "oooooo"      ==  "o"
periodo "sevilla"     ==  "sevilla"

Leer más…

El problema del número de emparejamiento de amigos consiste en calcular el número de formas de emparejar n amigos teniendo en cuenta que cada uno puede permanecer soltero o puede ser emparejado con algún otro amigo y que cada amigo puede ser emparejado sólo una vez. Por ejemplo, los 4 posibles emparejamientos de 3 amigos son

{1}, {2}, {3}
{1}, {2, 3}
{1, 2}, {3}
{1, 3}, {2}

Definir la función

nEmparejamientos :: Integer -> Integer

tal que (nEmparejamientos n) es el número de formas de emparejar a los n amigos. Por ejemplo,

nEmparejamientos 2   ==  2
nEmparejamientos 3   ==  4
nEmparejamientos 4   ==  10
nEmparejamientos 10  ==  9496
nEmparejamientos 30  ==  606917269909048576
length (show (nEmparejamientos3 (10^4)))  ==  17872

Leer más…

El problema de emparejamiento de amigos consiste en calcular las formas de emparejar n amigos teniendo en cuenta que cada uno puede permanecer soltero o puede ser emparejado con algún otro amigo y que cada amigo puede ser emparejado sólo una vez. Por ejemplo, los 4 posibles emparejamientos de 3 amigos son

{1}, {2}, {3}
{1}, {2, 3}
{1, 2}, {3}
{1, 3}, {2}

Definir la función

emparejamientos :: [Integer] -> [[[Integer]]]

tal que (emparejamientos n) es la lista de los posibles emparejamientos de los n amigos (numerados del 1 al n). Por ejemplo,

λ> emparejamientos [1..2]
[[[1],[2]],[[1,2]]]
λ> emparejamientos [1..3]
[[[1],[2],[3]],[[1],[2,3]],[[1,2],[3]],[[1,3],[2]]]

Leer más…

Una serie de potencias es una serie de la forma

a₀ + a₁x + a₂x² + a₃x³ + ...

Las series de potencias se pueden representar mediante listas infinitas. Por ejemplo, la serie de la función exponencial es

e^x = 1 + x + x²/2! + x³/3! + ...

y se puede representar por [1, 1, 1/2, 1/6, 1/24, 1/120, ...]

Las operaciones con series se pueden ver como una generalización de las de los polinomios.

En lo que sigue, usaremos el tipo (Serie a) para representar las series de potencias con coeficientes en a y su definición es

type Serie a = [a]