| Inicial | Temas | Sistemas | Cursos | Documentación

Tema 12: Búsqueda general en espacio de estados

Índice

En este tema se estudiará un procedimiento general de búsqueda que incluye a los procedimientos estudiados en el tema 8. Como caso de estudio se considerará el robot repartidor introducido en el tema 11.

1. El robot repartidor

1.1. Descripción del problema

  • El plano del dominio del robot repartidor es (Poole–98 p. 14)
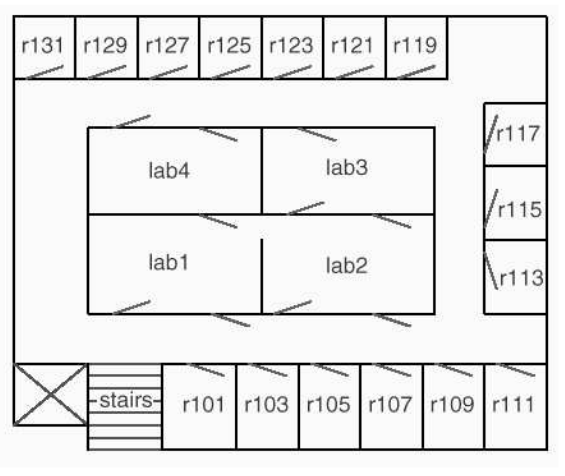
    tema-12-fig-1.png
  • El grafo del robot repartidor es (Poole–98 p. 14)
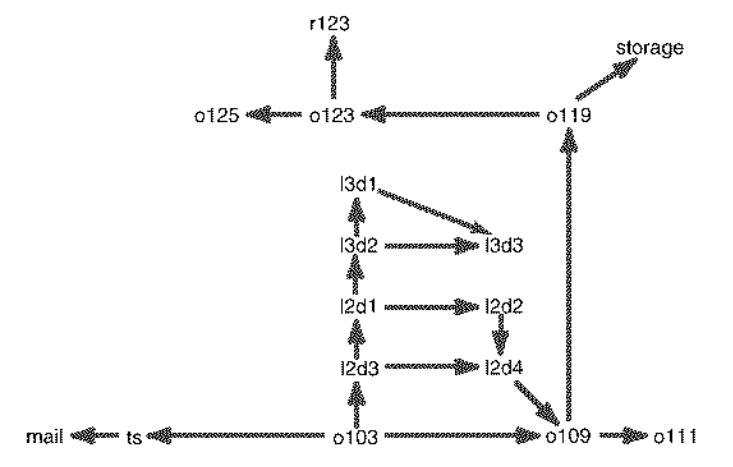
    tema-12-fig-2.png

  • Lenguaje para indicar la posición del robot:

    f103 en frente la habitación 103
    fe en frente la escalera
    correo en el correo
    l2p3 en la puerta 3 del laboratorio 2
    almacén en el almacén
    h123 en la habitación 123
  • El problema consiste en buscar un camino en el grafo desde f103 hasta h123.

1.2. Estado inicial

  • estado_inicial(?E) se verifica si E es el estado inicial. 

    estado_inicial(f103).

1.3. Estados finales

  • estado_final(?E) se verifica si E es un estado final. 

    estado_final(h123).

1.4. Sucesores

  • sucesor(+E1,?E2) se verifica si E2 es un sucesor del estado E1. 

    sucesor(f103,fe). 
sucesor(f103,l2p3). 
sucesor(f103,f109). 
sucesor(fe,correo). 
sucesor(f109,f111). 
sucesor(f109,f119). 
sucesor(f119,almacén). 
sucesor(f119,f123). 
sucesor(f123,h123). 
sucesor(f123,f125). 
sucesor(l2p1,l3p2). 
sucesor(l2p1,l2p2). 
sucesor(l2p2,l2p4). 
sucesor(l2p3,l2p1). 
sucesor(l2p3,l2p4). 
sucesor(l2p4,f109). 
sucesor(l3p2,l3p3). 
sucesor(l3p2,l3p1). 
sucesor(l3p1,l3p3).

1.5. Coste

  • coste(+E1,+E2,?C) se verifica si C es el coste de ir del estado E1 al E2. 

    coste(E1,E2,C) :-
   posicion(E1,X1,Y1),
   posicion(E2,X2,Y2),
   C is abs(X1-X2)+abs(Y1-Y2).

  • posicion(E,X,Y) se verifica si la posición del estado E es (X,Y). 

    posicion(correo,17,43).
posicion(fe,23,43).
posicion(f103,31,43).
posicion(f109,43,43).
posicion(f111,47,43).
posicion(f119,42,58).
posicion(f123,33,58).
posicion(f125,29,58).
posicion(h123,33,62).
posicion(l2p1,33,49).
posicion(l2p2,39,49).
posicion(l2p3,32,46).
posicion(l2p4,39,46).
posicion(l3p1,34,55).
posicion(l3p2,33,52).
posicion(l3p3,39,52).
posicion(almacén,45,62).

1.6. Heurística

  • heuristica(+E,?H) se verifica si H es la heurística del estado E. 

    heuristica(E,H) :-
   posicion(E,X,Y),
   estado_final(E1),
   posicion(E1,X1,Y1),
   H is abs(X-X1)+abs(Y-Y1).

1.7. Código

2. Procedimiento general de búsqueda

2.1. Procedimiento general de búsqueda

  • Relaciones dependientes del problema:
    • estado_inicial(E) se verifica si E es el estado inicial.
    • estado_final(E) se verifica si E es un estado final.
    • sucesor(E1,E2) se verifica si E2 es un estado sucesor de E1.
    • coste(E1,E2,C) se verifica si C es el coste de ir del estado E1 al E2.
    • heuristica(E,H) que se verifica si H es la heurística del estado E.
  • Datos:
    • Un nodo es una lista de estados [E(n),...,E(1)] de forma que E(1) es el estado inicial y E(i+1) es un sucesor de E(i)
    • Abiertos es una lista de nodos (los nodos pendientes de analizar)}

  • busqueda(+M,?S) se verifica si S es una solución del problema mediante búsqueda según el método M
    El procedimiento es

    • 1. Sea E el estado inicial.
    • 2. La solución S es la obtenida por búsqueda según el método M con [[E]] como la lista de abiertos.

    Su definición es 

    busqueda(M,S) :-
   estado_inicial(E),    % 1
   busqueda(M,[[E]],S).  % 2

  • busqueda(+M,+Abiertos,?S) se verifica si S es una solución encontrada por búsqueda según el método M a partir de las listas de Abiertos.
    El procedimiento es

    • 1. Si

      • 1.1. el primer elemento de Abiertos es [E|C] y
      • 1.2. E es un estado final,

      entonces

      • 1.3 S es la inversa de [E|C].

    • 2. Si

      • 2.1. N es un nodo de Abiertos (seleccionado según el método M) y R son los restantes nodos de Abiertos,
      • 2.2. Sucesores es la lista de los sucesores del nodo N,
      • 2.3. los nuevos abiertos, NAbiertos, es la lista obtenida expandiendo (según el método M) R con los Sucesores

      entonces

      • 2.4. S es la solución obtenida por búsqueda (según el método M) con los nuevos abiertos.

    Su definición es 

    busqueda(_M,Abiertos,S) :-
   Abiertos = [[E|C]|_],              % 1.1
   estado_final(E),                   % 1.2
   reverse([E|C],S).                  % 1.3
busqueda(M,Abiertos,S) :-
   selecciona(M,Abiertos,N,R),        % 2.1
   sucesores(N,Sucesores),            % 2.2
   expande(M,R,Sucesores,NAbiertos),  % 2.3
   busqueda(M,NAbiertos,S).           % 2.4

  • selecciona(+M,+LN1,?N,?LN2) se verifica si N es un nodo de la lista LN1 y LN2 es la lista de los restantes nodos. Se definirá en cada método. 

    :- discontiguous selecciona/4.

  • sucesores(+N,?L) se verifica si L es la lista de los sucesores del nodo N 

    sucesores([E|C],L) :-
   findall([E1,E|C],sucesor(E,E1),L).

  • expande(+M,+L1,+Sucesores,?L2) se verifica si L2 es la lista expandiendo (según el método M) la lista de nodos L1 con la lista de nodos Sucesores . Se definirá en cada método. 

    :- discontiguous expande/4.

2.2. Búsqueda en anchura

  • En la búsqueda en anchura se selecciona el primer nodo de Abiertos. 

    selecciona(anchura,[N|R],N,R).

  • En la búsqueda en anchura los sucesores se añaden al final de Abiertos. 

    expande(anchura,L1,Sucesores,L2) :-
   append(L1,Sucesores,L2).

  • Ejemplo: 

    ?- [busqueda, robot_repartidor].
true.

?- busqueda(anchura,S).
S = [f103,f109,f119,f123,h123] ;
S = [f103,l2p3,l2p4,f109,f119,f123,h123] 

?- trace(estado_final,+call).
true.

?- busqueda(anchura,S).
 T Call: estado_final(f103)
 T Call: estado_final(fe)
 T Call: estado_final(l2p3)
 T Call: estado_final(f109)
 T Call: estado_final(correo)
 T Call: estado_final(l2p1)
 T Call: estado_final(l2p4)
 T Call: estado_final(f111)
 T Call: estado_final(f119)
 T Call: estado_final(l3p2)
 T Call: estado_final(l2p2)
 T Call: estado_final(f109)
 T Call: estado_final(almacén)
 T Call: estado_final(f123)
 T Call: estado_final(l3p3)
 T Call: estado_final(l3p1)
 T Call: estado_final(l2p4)
 T Call: estado_final(f111)
 T Call: estado_final(f119)
 T Call: estado_final(h123)
S = [f103,f109,f119,f123,h123] 

?- trace(estado_final,-all).
true.

2.3. Búsqueda en profundidad

  • En la búsqueda en profundidad se selecciona el primer nodo de Abiertos. 

    selecciona(profundidad,[N|R],N,R).

  • En la búsqueda en profundidad los sucesores se añaden al principio de Abiertos. 

    expande(profundidad,L1,Sucesores,L2) :-
   append(Sucesores,L1,L2).

  • Ejemplo: 

    ?- busqueda(profundidad,S).
S = [f103,l2p3,l2p1,l2p2,l2p4,f109,f119,f123,h123] 

?- trace(estado_final,+call).
true.

?- busqueda(profundidad,S).
 T Call: estado_final(f103)
 T Call: estado_final(fe)
 T Call: estado_final(correo)
 T Call: estado_final(l2p3)
 T Call: estado_final(l2p1)
 T Call: estado_final(l3p2)
 T Call: estado_final(l3p3)
 T Call: estado_final(l3p1)
 T Call: estado_final(l3p3)
 T Call: estado_final(l2p2)
 T Call: estado_final(l2p4)
 T Call: estado_final(f109)
 T Call: estado_final(f111)
 T Call: estado_final(f119)
 T Call: estado_final(almacén)
 T Call: estado_final(f123)
 T Call: estado_final(h123)
S = [f103,l2p3,l2p1,l2p2,l2p4,f109,f119,f123,h123] 

?- trace(estado_final,-all).
true.

2.4. Búsqueda optimal

2.4.1. Valor de los nodos

  • valor(+M,+N,?V) se verifica si el valor (según el método M) del nodo N es V. Se define en cada método. En la búsqueda optimal es coste del camino. 

    :- discontiguous valor/3. 

valor(optimal,N,V) :-
   coste_camino(N,V).

  • coste_camino(+N,?V) se verifica si V es el coste del camino representado por el nodo N. 

    coste_camino([_E],0).
coste_camino([E2,E1|R],V) :-
   coste(E2,E1,V1),
   coste_camino([E1|R],V2),
   V is V1+V2.

2.4.2. Selección

  • En la búsqueda optimal se selecciona el nodo de Abiertos de menor valor. 

    selecciona(optimal,LN1,N,LN2) :-
   selecciona_con_valor(optimal,LN1,N,LN2).

  • selecciona_con_valor(+M,+LN1,?N,?LN2) se verifica si N es el mejor nodo (según el método M) de la lista LN1 y LN2 es la lista de los restantes nodos. 

    selecciona_con_valor(M,LN1,N,LN2) :-
   member(N,LN1),
   valor(M,N,V),
   not(member(N1,LN1),
       valor(M,N1,V1),
       V1 < V),
   select(LN1,N,LN2).

2.4.3. Expansión

  • En la búsqueda optimal los sucesores se añaden al final de Abiertos. 

    expande(optimal,L1,Sucesores,L2) :-
   append(Sucesores,L1,L2).

2.5. Búsqueda por primero el mejor

  • En la búsqueda por primero el mejor, el valor de un nodo es la heurística del primero de sus estados. 

    valor(primero_el_mejor,[E|_R],V) :-
   heuristica(E,V).

2.5.1. Selección

  • En la búsqueda por primero el mejor se selecciona el nodo de Abiertos de menor valor (es decir, de menor heurística). 

    selecciona(primero_el_mejor,LN1,N,LN2) :-
   selecciona_con_valor(primero_el_mejor,LN1,N,LN2).

2.5.2. Expansión

  • En la búsqueda por primero el mejor los sucesores se añaden al principio de Abiertos. 

    expande(primero_el_mejor,L1,Sucesores,L2) :-
   append(Sucesores,L1,L2).

2.6. Búsqueda por A*

2.6.1. Valor

  • En la búsqueda A* el coste de un nodo es la suma del coste de su camino más la heurística. 

    valor(a_estrella,[E|R],V) :-
   coste_camino([E|R],V1),
   heuristica(E,V2),
   V is V1+V2.

2.6.2. Selección

  • En la búsqueda A* se selecciona el nodo de Abiertos de menor valor (es decir, de menor coste del camino más heurística). 

    selecciona(a_estrella,LN1,N,LN2) :-
   selecciona_con_valor(a_estrella,LN1,N,LN2).

2.6.3. Expansión

  • En la búsqueda A* el mejor los sucesores se añaden al principio de Abiertos. 

    expande(a_estrella,L1,Sucesores,L2) :-
   append(Sucesores,L1,L2).

2.7. Código

  • El código del procedimiento general de búsqueda se encuentra en busqueda.pl.

3. Procedimiento general de búsqueda sin reevaluaciones

3.1. Procedimiento general de búsqueda con valores

  • Datos:
    • Un nodo es un término V-[E(n),...,E(1)] de forma que E(1) es el estado inicial, E(i+1) es un sucesor de E(i) y V es el valor de [E(n),...,E(1)] según el procedimiento de búsqueda.
    • Abiertos es una lista de nodos (los nodos pendientes de analizar).}

  • busqueda(+M,?S) se verifica si S es una solución del problema mediante búsqueda según el método M.
    Procedimiento:

    • 1. Sea E el estado inicial y
    • 2. sea V el valor de la extensión del nodo 0-[] con el estado E
    • 3. La solución S es la obtenida por búsqueda en anchura con [V-[E]] como la lista de abiertos.

    Su definición es 

    busqueda(M,S) :-
   estado_inicial(E),      % 1
   valor(M,0-[],E,V),      % 2
   busqueda(M,[V-[E]],S).  % 3

  • valor(+M,+N,+E,?V) se verifica si el valor (según el método M) de la extensión del nodo N con el estado E es V. Se define en cada método. 

    :- discontiguous valor/3.

  • busqueda(+M,+Abiertos,?S) se verifica si S es una solución encontrada por búsqueda según el método M a partir de las listas de Abiertos. 

    busqueda(_M,Abiertos,S) :-
   Abiertos = [_-[E|C]|_],            % 1.1
   estado_final(E),                   % 1.2
   reverse([E|C],S).                  % 1.3
busqueda(M,Abiertos,S) :-
   selecciona(M,Abiertos,N,R),        % 2.1
   sucesores(M,N,Sucesores),          % 2.2
   expande(M,R,Sucesores,NAbiertos),  % 2.3
   busqueda(M,NAbiertos,S).           % 2.4

  • selecciona(+M,+LN1,?N,?LN2) se verifica si N es el primer nodo de la lista LN1 y LN2 es la lista de los restantes nodos. 

    selecciona(_M,[N|R],N,R).

  • sucesores(+N,?L) se verifica si L es la lista de los sucesores del nodo N. 

    sucesores(M,V-[E|C],L) :-
   findall(V1-[E1,E|C],
          (sucesor(E,E1),valor(M,V-[E|C],E1,V1)),
          L).

  • expande(+M,+L1,+Sucesores,?L2) se verifica si L2 es la lista obtenida expandiendo (según el método M) la lista de nodos L1 con la lista de nodos ~Sucesores, ordenada por sus valores. 

    expande(_M,L1,Sucesores,L2) :-
   append(Sucesores,L1,L3),
   sort(L3,L2).

3.2. Búsqueda optimal

  • El valor en la búsqueda optimal es el coste del camino. 

    valor(optimal,0-[],_E,0).
valor(optimal,V-[E|_C],E1,V1) :-
   coste(E,E1,V2),
   V1 is V+V2.

3.3. Búsqueda por primero el mejor

  • El valor en la búsqueda por primero el mejor es la heurística. 

    valor(primero_el_mejor,_N,E,V) :-
   heuristica(E,V).

3.4. Búsqueda A*

  • El valor en la búsqueda A* es la suma del coste del camino y la heurística. 

    valor(a_estrella,0-[],E,H+0) :-
   heuristica(E,H).
valor(a_estrella,_F+C-[E|_R],E1,F1+C1) :-
   coste(E,E1,C2),
   C1 is C+C2,
   heuristica(E1,H),
   F1 is C1+H.

3.5. Ejemplos

  • Ejemplos de búsquedas con valores 

    ?- [busqueda_con_valores, robot_repartidor].
true.

?- busqueda(optimal,S).
S = [f103,f109,f119,f123,h123] 
?- busqueda(primero_el_mejor,S).
S = [f103,f109,f119,f123,h123] 
?- busqueda(a_estrella,S).
S = [f103,f109,f119,f123,h123]

3.6. Código

4. Refinamientos de estrategias de búsqueda

  • El procedimiento general de búsqueda se puede refinar:
    • Eliminando ciclos.
    • Eliminando caminos múltiples.
  • El procedimiento general de búsqueda se puede ampliar para incluir:
    • Búsqueda por profundidad acotada.
    • Búsqueda en profundidad iterativa.
    • Búsqueda en haz.
    • Búsqueda en escalada.

5. Bibliografía

| Inicial | Temas | Sistemas | Cursos | Documentación

José A. Alonso Jiménez

Sevilla, 12 de julio del 2025

Licencia: Creative Commons.